Оглавление

Раздел IX. Определенный интеграл 4

Задача о площади криволинейной трапеции 5

Формула Ньютона-Лейбница 8

Свойства определенного интеграла 11

Геометрический смысл определенного интеграла 14

Замена переменной и интегрирование по частям в определенном интеграле 20

Некоторые приложения определенного интеграла 27

Несобственные интегралы 33

Раздел X. Дифференциальные уравнения 43

Дифференциальные уравнения первого порядка 44

Уравнения в дифференциалах 49

Уравнение с разделенными переменными 53

Уравнение с разделяющимися переменными 56

Однородное уравнение 70

Линейное уравнение 75

Дифференциальные уравнения второго порядка 81

Уравнения, допускающие понижение порядка 84

96

Линейные дифференциальные уравнения второго порядка 96

Линейные дифференциальные уравнения с постоянными коэффициентами 103

Раздел IX. Определенный интеграл

Пройденный нами неопределенный интеграл применяется, в основном, как инструмент, причем в двух основных направлениях. Во-первых, он помогает вычислению так называемого определенного интеграла (к его определению мы сейчас и приступим), который и имеет разнообразнейшие практические приложения во всех областях деятельности. Во-вторых, неопределенный интеграл помогает решать так называемые дифференциальные уравнения, с которыми мы познакомимся в следующей теме.

Многие из основных понятий математики возникли из необходимости решения практических задач, возникающих в человеческой деятельности. Так, например, к понятию производной привела задача нахождения (мгновенной) скорости при неравномерном движении. Вторая производная соответствует понятию ускорения в конкретный момент времени. Понятие (определенного) интеграла родилось из традиционной задачи вычисления площадей разнообразных фигур. Средствами элементарной математики удавалось найти формулы только фигур, граница которых состоит из отрезков прямых (треугольник, прямоугольник, параллелограмм, трапеция и т.п. ). Однако на практике возникала задача вычисления площади фигур с произвольными криволинейными границами. Из этой задачи и родилось понятие определенного интеграла. Мы тоже придем к необходимости такого понятия, рассмотрев задачу о вычислении площади фигуры (так называемой криволинейной трапеции), у которой одна (для начала) граница криволинейна.

Задача о площади криволинейной трапеции

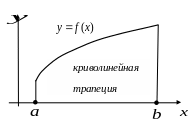
Рассмотрим на координатной плоскости хОу следующий четырехугольник с одной криволинейной границей. Основанием четырехугольника является некоторый отрезок [a,b] на числовой оси х. Боковыми сторонами являются отрезки вертикальных прямых, проходящих через точки (числа) a и b на оси х. А вот верхнее основание сделаем криволинейным. Но надо эту кривую границу как-то определить. Мы помним, что разнообразные кривые нам давали графики различных функций. Поэтому будем считать, что верхнее основание есть кусок графика некоторой функции , непрерывной на отрезке [a,b]. Такой «четырехугольник» называется криволинейной трапецией (см. рисунок). Поставим себе задачу найти формулу для вычисления его площади, которую обозначим буквой S. Поскольку точной формулы для вычисления площади такой фигуры у нас нет, то на первом этапе поставим целью найти хотя бы приближенную формулу для S. Идея такая. Попробуем достаточно плотно заполнить криволинейную трапецию, например, прямоугольниками (так как формула для вычисления их площадей известна) и посчитаем сумму их площадей. Получим приближенное (так как эти прямоугольники не смогут заполнить всю криволинейную трапецию) значение для S. Прямоугольники построим следующим образом. Разделим отрезок [a,b] на n равных частей точками a = x₀ < x₁ < x₂ < … < x_n = b (см. рисунок, соответствующий n=5). Число разбиений n потом будет меняться. Проведем через каждую точку деления (узел) вертикальный отрезок до пересечения с графиком функции .Тогда вся криволинейная трапеция разобьется на n маленьких криволинейных трапеций, площади которых обозначим S₁, S₂,…, S_n . Тогда ясно, что S= S₁+ S₂+…+ S_n . Эти площади мы тоже не умеем вычислять, так как маленькие трапеции тоже содержат криволинейную границу. Но п реимущество каждой из них в том, что криволинейные границы у них значительно меньше, чем у исходной криволинейной трапеции. Сейчас мы их вообще уберем, заменив маленькие криволинейные трапеции прямоугольниками (как на рисунке). Площадь прямоугольника равна произведению длин его сторон. Длина нижнего основания у всех прямоугольников одинакова и равна h = (b−a)/n (так как отрезок делился на n равных частей). Из рисунка видно, что длина второй стороны первого прямоугольника равна значению функции в точке . Для второго прямоугольника длина этой стороны равна и т.д. . Площадь первой криволинейной трапеции приближенно равна площади первого прямоугольника: . Далее, , … , . Подставляя эти приближенные равенства в приведенную выше формулу S= S₁+ S₂+…+ S_n , получим приближенную формулу для площади всей криволинейной трапеции: . Вынося h за скобку и подставляя его значение h = (b−a)/n , получаем . Выражение

в правой части этого приближенного равенства называется интегральной суммой для функции , соответствующей данному разбиению. Попробуем превратить приближенное равенство для площади криволинейной трапеции S в точное. Равенство оказалось приближенным, поскольку, как видно из рисунка, остались неучтенными площади «криволинейных» треугольников под графиком функции, площади которых и не учитываются в приведенной приближенной формуле.

Посмотрим, как поведет себя величина этой погрешности, если, скажем, увеличить число разбиений исходного отрезка вдвое (вместо n взять 2n). Тогда в середину каждого старого отрезка попадет еще один узел. Легко убедиться, что в этом случае часть неучтенных площадей старых «криволинейных» треугольников учтется, а новая приближенная формула окажется более точной. И чем больше берется число разбиений, тем точнее становится формула. Если перейти в этой формуле к пределу при n → ∞, то в пределе «криволинейные» треугольники исчезнут, а формула для площади окажется точной. Итак, площадь криволинейной трапеции есть предел интегральных сумм, когда число разбиений отрезка [a,b] стремится к бесконечности, и выражается точной формулой:

(1) .

Хотя мы и получили точную формулу для площади криволинейной трапеции, она мало пригодна для практического применения по следующим причинам. Во-первых, мы никогда не сможем взять n = ∞, мы можем взять n только конечным (хотя и большим), а потому нам опять останется возможность пользоваться только приближенной формулой . Во-вторых, если мы возьмем число n очень большим (чтобы погрешность приближенной формулы стала маленькой), то нам придется вычислить сумму большого числа слагаемых, каждое из которых есть значение функции в некоторой точке. Если эта функция вычисляется по громоздкой формуле, то нас ждет слишком утомительная вычислительная работа. Поэтому исторически возникала необходимость найти простой способ вычисления пределов вида в правой части (1) . Такой способ был найден практически одновременно известными математиками Ньютоном и Лейбницем, а сами такие пределы получили название определенного интеграла. Перейдем к точным определениям.

Пусть функция непрерывна на отрезке [a,b]. Определенным интегралом от функции на отрезке [a,b] называется предел интегральных сумм , когда число разбиений отрезка стремиться к бесконечности. Обозначение такого интеграла: . Итак, по определению:

(2) .

Числа и называются нижним и верхним пределами интегрирования.

Замечание. В большинстве учебников дается более общее и более сложное определение определенного интеграла. Однако для непрерывных функций эти определения эквивалентны, а именно такие функции мы пока и рассматриваем.

Сравнивая точную формулу (1) для площади S криволинейной трапеции и формулу (2), определяющую интеграл, можно записать:

(3) .