10.5. Туннельный эффект

Качественное различие свойств макроскопического тела и микрочастицы особенно ярко проявляется в поведении их при встрече с потенциальным барьером. Рассмотрим простейший случай, когда потенциальный барьер имеет вид ступеньки высотой U₀ и бесконечной длины (рис. 10), т.е. когда потенциальная энергия частицы

При такой потенциальной энергии классическая частица, двигаясь вдоль оси X слева направо, и имея полную энергию E, либо беспрепятственно пройдет над барьером (при E > U₀), либо отразится от него (при E < U₀) и будет двигаться в обратном направлении. В области, где E < U₀, классическая частица проникнуть не может, так как в этой области ее кинетическая энергия была бы K = E – –U₀ < 0, что физически абсурдно. Не так обстоит дело для микрочастицы. У микрочастицы имеется отличная от нуля вероятность того, что микрочастица отразится от барьера и будет двигаться в обратную сторону при E > U₀ и имеется также отличная от нуля вероятность того, что микрочастица проникнет под потенциальный барьер, т.е. окажется в области x > 0 при E < U₀. Это непосредственно вытекает из решения уравнения Шредингера. Для области x > 0 это уравнение имеет вид

или

где Решением этого уравнения, удовлетворяющем условию конечности, является функция вида

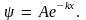
Это есть волновая функция частицы в области с энергией E < U₀. Вероятность обнаружить частицу под барьером на расстоянии x

B

где Если барьер имеет конечную ширину, равную d, то вероятность его прохождения частицей, имеющей энергию E < < U₀, будет

(10.)

Как видим, эта вероятность тем больше, чем меньше ширина барьера d и чем меньше его превышение над E, т.е. разность U₀ – E. Тем самым мы показали, что квантовая частица, в отличие от классической, может проходить сквозь потенциальный барьер, т.е. сквозь область, где ее полная энергия меньше потенциальной. Это явление называется туннельным эффектом.

Формулу (10.) можно переписать в виде

_где А – постоянная, k / 2 – длина, на которой вероятность проникновения уменьшается в e раз, причем

Парадокс (с точки зрения классической физики) туннельного эффекта (в области E < U₀ кинетическая энергия частицы K < 0) объясняется тем, что в квантовой механике полную энергию частицы нельзя разделить на ее кинетическую и потенциальную энергии, так как из-за принципа неопределенности эти энергии не имеют одновременно определенного значения. Действительно, так как потенциальная энергия частицы зависит от ее координат, а кинетическая – от проекций ее импульса,

а координаты и соответствующие проекции импульса одновременно не определены, то одновременно не определены и потенциальная и кинетическая энергии. Поэтому если, например, в какой-либо точке x₀ под барьером потенциальная энергия частицы строго фиксирована U = U(x₀), то ее кинетическая энергия полностью не определена, а значит, нельзя сказать, что она определенно отрицательная.

10.6. Квантовый гармонический осциллятор

Классический гармонический осциллятор, как известно, представляет собой частицу (материальную точку) массой m, совершающую гармонические колебания под действием квазиупругой силы , где ω – собственная частота колебаний осциллятора. Потенциальная энергия такой частицы

(10.13)

Квантовым гармоническим осциллятором называют микрочастицу, гармонически колеблющуюся в области пространства атомных размеров. Потенциальная энергия такого осциллятора так же определяется выражением (10.13). Задача о колебаниях квантового осциллятора решается с помощью уравнения Шредингера

(10.14)

Зависимость потенциальной энергии от величины смещения x, определяемая функцией (10.13), имеет вид параболы, т.е. потенциальная яма имеет параболический профиль. При заданной полной энергии E > 0 классическая частица движется в ограниченной области пространства между точками x_1,2 = A, где A – амплитуда колебаний, определяемая из условия

откуда

В квантовой механике -функция осциллятора из-за туннельного эффекта отлична от нуля и вне указанных пределов. Однако ввиду того, что с ростом x в области где E < U, увеличивается также и разность U – E, то вероятность, а с ней и волновая -функция, должны резко убывать с удалением частицы от положения равновесия, т.е. при

Нахождение волновой -функции из решения уравнения (10.14) довольно сложно. Легко определить вид 𝜓-функции на большом расстоянии от начала координат, т.е. при Для больших x уравнение (10.14) переходит в уравнение где Решением этого уравнения в рассматриваемой области будет

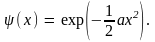
Поэтому решение исходного уравнения (10.14) можно искать в виде

Где A – постоянная, определяемая из условия нормировки волновой функции, – многочлен, составленный из функций вида Cxⁿ; он должен быть таким, чтобы не изменить свойство -функции при

Можно показать, что указанное требование, предъявляемое к волновой функции, будет удовлетворяться при значениях энергии (параметра E)

(10.15)

где n – любое целое положительное число, включая нуль. Его называют квантовым числом осциллятора, или колебательным квантовым числом. Каждому значению n отвечает определенная волновая функция поэтому квантовое число n определяет квантовое состояние линейного гармонического осциллятора. Например, значению n = 0 соответствует волновая функция значению n = 1 – волновая функция и т.д.

Из формулы (10.15) видно, что энергия колеблющейся микрочастицы является квантованной (энергетический спектр дискретный). Так и должно быть, поскольку движение частицы является финитным. Уровни энергии осциллятора представлены на рис. 10., где пунктиром показана зависимость потенциальной энергии осциллятора, даваемая формулой (10.13). Так как каждому значению n соответствует одно значение энергии E_n и одна волновая функция то все уровни осциллятора не вырождены. Расстояние между любыми соседними уровнями одинаково и равно Так как ΔE = const, то говорят, что уровни энергии осциллятора эквидистантны. Величину называют квантом энергии осциллятора.

При n = 0 энергия Эта наименьшая возможная энергия осциллятора является его нулевой энергией. Колебания с такой энергией называют нулевыми колебаниями. Как видим, упруго связанная частица, обладая нулевой энергией, не покоится в точке x = 0 (в положении равновесия). Вероятность найти ее на расстоянии x, определяемая как не равна нулю. При этом, чем больше нулевая энергия, а значит, чем больше параметр тем быстрее убывает функция и тем, следовательно, меньше вероятность найти частицу на большом расстоянии от точки равновесия, и тем в меньшем объеме находится частица. Мы видим, что, как и в задаче с частицей в потенциальной яме, нулевая энергия тем больше, чем в меньшем объеме оказывается частица.

В основном состоянии (n = 0) наиболее вероятно найти частицу в точке равновесия x = 0. Классическим аналогом этого состояния является состояние покоя. Квадрат модуля собственной функции для состояния, отвечающего n = 1, с энергией имеет максимум на некотором расстоянии от центра колебаний. Классическим аналогом этого состояния является колебание частицы с определенной амплитудой.

В классическом пределе – квантование энергии исчезает, колеблющаяся частица может обладать любой энергией; исчезает и нулевая энергия (E₀ = 0). Квантование энергии исчезает и при очень больших вантовых числах:

при