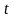3.8. Обращение хода времени в механике

Рассмотренное ранее свойство одноаправленности времени никак не проявляет себя в механике: уравнение движения инвариантно относительно обращения или отражения времени, математически определяемого подстановкой Δt → Δt′ = –Δt, а значит, dt → dt′ = –dt. Покажем это:

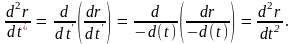
В простейшем случае чисто механической системы сила, действующая на материальную точку, зависит только от взаимного расстояния между точками, т.е. сила F(r) – инвариант указанного преобразования. Подробный анализ всех механических сил, в том числе электромагнитных, показывает, что все они инвариантны по отношению к обращению хода времени. Следовательно, при обращении времени, т.е. замене 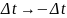, вид уравнения движения не изменяется. Уравнение движения оказывается инвариантным по отношению к обращению времени. Отсюда следует, что функция r = r(–t) также является решением уравнения (3.9). Но из первого уравнения (3.12) следует, что при указанной замене скорость

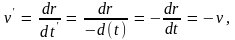
Это означает, что замена эквивалентна замене 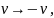т.е. обращению направления скорости. Поэтому функция r = r(–t) описывает движение материальной точки, обратное движению, описываемому функцией r = r(t). Следовательно, каково бы ни было движение тела, всегда возможно обратное движение, т.е. движение, при котором тело проходит через те же точки пространства и с теми же скоростями, что и в прямом движении, но только в обратном направлении. Пусть, например, тело брошено под некоторым углом к горизонту; описав определенную траекторию (в отсутствие сопротивления воздуха – параболу) оно упадет на Землю в некотором месте. Если теперь бросить тело из этого места под тем же углом, под которым оно упало, и с той же скоростью, то тело опишет ту же траекторию, только в обратном направлении и упадет в первоначальном месте (при условии, что сопротивлением воздуха можно пренебречь).

Таблица 1

t	0	1	2	3	4	5	6
v	0	1	2	3	4	5	6
x	0	0,5	2	4,5	8	12,5	18

Таблица 2

	6	5	4	3	2	1	0
v′	–6	–5	–4	–3	–2	–1	0
x′	18	12,5	8	4,5	2	0,5	0

Проиллюстрируем обратимость механического движения простым примером. Пусть в некоторой системе S на материальную точку, находящуюся в состоянии покоя, начинает действовать постоянная направленная вдоль оси X сила, которая сообщает точке ускорение а. В таком случае точка будет двигаться по оси X равноускоренно в соответствии с формулами v = at, x = at²/2. В системе S′ с обращенным временем, где Δt′ = –Δt, сила и ускорение остаются теми же, а направление скорости меняется на противоположное. Пусть в системе S к моменту времени t₀ точка достигла скорости v₀ = at₀ и переместилась в точку с координатой x₀ = = at₀²/2. Рассматривая ее движение в системе S′ с этого момента времени как начального, т.е. 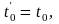будем иметь

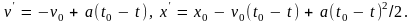
Это равнозамедленное движение по оси X осуществляется вспять. В таблице1, составленной для a = 1м/с² и t₀ = 6с, представлен расчет скорости и координаты при прямом движении (в системе S), а в таблице 2 – тех же величин при движении с обращенным временем (в системе S′)

Из сравнения таблиц 1 и 2 видно, что материальная точка проходит рассмотренные в системе S положения с той же скоростью в обратном порядке и возвращается в исходную точку (x = 0).

Если снять на кинопленку какое-либо механическое движение тела, например, рассмотренное выше прямолинейное движение вдоль оси X, а затем прокрутить ленту в обратном направлении (что равносильно обращению времени), то мы увидим движение, которое можно наблюдать в действительности. Такое движение вполне реально; его можно получить, если на пути тела поставить упругую стенку. Тело, отразившись от нее, будет двигаться в обратном направлении. Если же проделать то же самое в отношении любых других физических макропроцессов, то мы увидим другой, не наблюдаемый в действительности физический процесс. Обратимыми являются только механические движения без трения и сопротивления.

.

1 Подробно о деформациях тел будет говорится в главе 7.