3.7. Уравнения движения материальной точки

Основной закон динамики материальной точки можно записать в виде дифференциального уравнения. Заменяя в выражении (3.2) вектор ускорения кинематическим соотношением 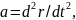получим

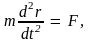(3.9)

При этом сила, действующая на материальную точку, может зависеть как от положения материальной точки (r) и времени (t), но и от ее относительной скорости v: F = F(r, t, v). Если эта функция известна, говорят, что задан закон действия силы.

Линейное дифференциальное уравнение второго порядка (3.9) и называется уравнением движения материальной точки в векторной форме. Запишем его также в более компактном виде:

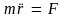(3.10)

Проецируя векторы, входящие в это уравнение, на координатные оси X, Y, Z, получим уравнения движения материальной точки в координатной форме

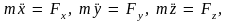(3.11)

где F_x, F_y и F_z – проекции вектора силы, действующей на материальную точку, на координатные оси X, Y и Z соответственно. В математическом отношении уравнение (3.9) (или (3.10)) является дифференциальным уравнением относительно векторной функции r(t), а уравнения (3.11) – уравнениями относительно скалярных функций x(t), y(t) и z(t).

Уравнения движения позволяют решить две основные задачи динамики материальной точки.

1. Зная массу материальной точки и ее закон движения, т.е. зависимость радиус-вектора точки или ее координат от времени, r = = r(t), найти действующую на точку силу.

2. По заданной массе m точки и закону, действующей на нее силы определить закон движения материальной точки.

Решение первой задачи сводится к двукратному дифференцированию по времени векторной функции r(t) или скалярных функций x(t). y(t), z(t) и последующему умножению полученного результата на массу тела m.

Вторая задача решается путем двух последовательных интегрирований по времени либо векторного уравнения (3.9), если сила задана в векторной форме, либо уравнений (3.11), если заданы компоненты силы

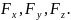
Рассмотрим случай, когда сила задана в векторной форме. В этом случае закон движения ищется в векторной форме, т.е. определяется функция r = r(t) с помощью уравнения (3.9). При этом уравнение (3.10) удобно заменить двумя векторными уравнениями, являющимися дифференциальными уравнениями первого порядка:

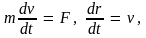(3.12)

или (в компактной форме)

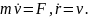(3.13)

Поэтому решение задачи можно разбить на два этапа: сначала, проинтегрировав первое уравнение (3.12), получим функцию v(t), а затем, подставив эту функцию во второе уравнение (3.12) и проинтегрировав его, найдем закон движения r(t). При интегрировании каждого из уравнений (3.12) появляются по одной неопределенной постоянной C₁ и C₂ – постоянные векторы. Эти постоянные интегрирования войдут в общее решение уравнения (3.9), вследствие чего это общее решение будет иметь вид r = r(t, C₁, C₂). Чтобы довести решение каждой конкретной задачи до конца, надо определить значения постоянных C₁ и C₂. Для определения этих векторов уравнение движения (3.9) следует дополнить двумя условиями, в качестве которых берут значение скорости точки и ее радиус-вектора в какой-либо момент времени t₀ (обычно в момент начала действия силы, который принимают за начальный (t₀ = 0), т.е. указывают значение скорости v и радиус-вектора r при t₀ = 0: v(0) = v₀, r(0) = r₀. Эти условия называются начальными условиями. Следовательно, закон движения материальной точки с помощью уравнения (3.9) можно определить, если во 1-х, известна сила, действующая на точку и во 2-х, если заданы начальные условия.

Мы видим, что задание силы еще не определяет однозначно движение материальной точки, а определяет целый класс однотипных движений, различающихся между собой характеристическими параметрами – векторами C₁ и C₂. Действующая сила определяет только ускорение движущейся точки, а скорость и положение точки на траектории (и сама траектория) могут зависеть еще от скорости, которая сообщена точке в начальный момент, и от начального положения точки. Так, например, материальная точка, двигаясь вблизи поверхности земли под действием силы тяжести, имеет ускорение g, если не учитывать сопротивление воздуха. Но точка будет иметь различные скорости и положения в пространстве в один и тот же момент времени и различную форму в зависимости от того, из какой точки пространства началось движение и с какой по величине и направлению начальной скоростью. Для выделения конкретного вида движения точки и задают ее начальные условия.

Движущаяся материальная точка характеризуется в каждый момент времени координатами и проекциями скорости (или импульса). Эти величины называются механическими параметрами точки. Если эти параметры заданы, говорят, что определено механическое состояние материальной точки.

Как мы видели, уравнения движения позволяют определить положение и скорость материальной точки – механическое состояние точки в данный момент времени t по известным силам , действующим на точку , и ее состоянию в начальный, вообще любой предшествующий момент времени t₀ < t. Этот факт выражает собой принцип причинности в классической механике. Считается, что состояние материальной точки в момент времени t₀ является причиной ее состояния в последующий момент времени t. Уравнения движения позволяют решить задачу о движении точки не только для момента времени t > t₀, но и для момента времени t < < t₀. Другими словами, с помощью уравнений движения, зная состояние материальной точки в данный момент времени, можно не только предсказать дальнейшее движение точки, но ретросказать ее движение, т.е. восстановить ее движение в предшествующие моменты времени. Все сказанное относится не только к одной материальной точке, но и к системе материальных точек.

Сила, действующая на материальную точку, одинакова во всех движущихся друг относительно друга системах отсчета. Это следует из того, что сила зависит от расстояния между взаимодействующими материальными точками (и, может быть, от относительной скорости), а эти расстояния (и относительные скорости) в ньютоновской механике считаются одинаковыми во всех инерциальных системах отсчета. Таким образом, F = F′, где F и F′ – силы, действующие на материальную точку в системах отсчета S и S′ соответственно. Ускорения и масса тела также одинаковы во всех инерциальных системах отсчета. Поэтому если ma = F – в системе отсчета S, то ma′ = F′ – в системе отсчета S′. Это означает, что уравнения движения классической механики являются инвариантными по отношению к преобразованиям Галилея.

Покажем, что уравнение движения классической механики в форме (3.9) является следствием существования инерциальных систем отсчета и принципа относительности.

Предположим, что уравнение движения материальной точки выражается некоторой вектор-функцией Ф, зависящей от радиус-вектора r материальной точки, времени t и производных радиус-вектора по времени первого, второго, третьего и т.д. порядков. Принцип относительности и свойства симметрии пространства и времени накладывают ограничения на число переменных, входящих в функцию Ф. Поскольку уравнение движения должно быть инвариантным относительно преобразования сдвига в пространстве 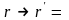r + a, где a = const – вектор трансляции (сдвига), то оно не должно содержать радиус-вектор r материальной точки, иначе это уравнение при указанном преобразовании изменит свой вид. Точно также, инвариантность уравнения движения по отношению к преобразованию сдвига во времени, 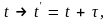где 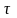= const (сдвиг во времени), исключает явную зависимость уравнения движения от времени t. Инвариантность уравнения движения по отношению к преобразованию скорости 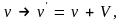где – скорость движения системы отсчета, т.е. принцип относительности, требует исключения из числа аргументов первую производную радиус-вектора по времени (скорость материальной точки).

Следует учесть также уникальность инерциальных систем отсчета. Этот класс систем отсчета определяется исключительно только их скоростью V и не зависит от высших производных 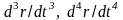b и т.д. Поэтому функция Ф не может зависеть от производных более высокого порядка, чем вторая.

Предположим теперь, что существует один параметр m, характеризующий материальную точку. Тогда функция Ф запишется в виде 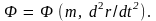Сделав простейшее допущение, что этот параметр и производная 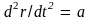входят в функцию Ф в виде произведения (мультипликативно), получим 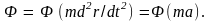Определив, далее, произведение 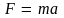как силу, действующую на материальную точку, придем ко второму закону динамики и к уравнению (3.9).