3.6. Принцип эквивалентности. Пространство и время в общей теории относительности

Важнейшим свойством сил инерции, является то, что эти силы, подобно силе тяжести, пропорциональны массе тела, а ускорения, вызываемые ими, от массы тела не зависят. Поэтому в однородном поле сил инерции, как и в однородном поле сил тяжести, все тела движутся с одним и тем же ускорением, независимо от их масс. Отсюда следует, что если, находясь в закрытой лаборатории, мы замечаем, что все тела независимо от их масс падают с одинаковым ускорением, то мы не сможем на основании только этого факта установить, чем вызвано это ускорение – силами тяжести, ускоренным движением системы отсчета (лаборатории) или обеими этими причинами вместе. Если g = – a, а гравитационная масса равна инертной, то любое движение тела (при наличии каких угодно добавочных сил) в неинерциальной системе отсчета происходит точно так же, как движение тела в инерциальной системе при наличии в ней гравитационного поля напряженности g. Подтверждением неотличимости сил инерции и однородных сил тяжести могут служить также рассмотренные выше явление невесомости и явление перегрузки. Если система отсчета движется вниз с ускорением g, то любое тело а этой системе отсчета будет неподвижным. Ускорение системы компенсирует силу гравитационного притяжения к земле. Никакими опытами по механическому движению тел невозможно отличить силы тяжести от сил инерции. Согласно Эйнштейну, это невозможно сделать вообще никакими физическими опытами. Это предположение, возведенное Эйнштейном в постулат, составляет содержание так называемого принципа эквивалентности сил тяготения и сил инерции: все физические явления в однородном поле сил тяготения происходят совершенно так же, как и в соответствующем однородном поле сил инерции. Этот постулат лежит в основе общей теории относительности, называемой также релятивистской теорией тяготения. Принцип эквивалентности основан на утверждении о равенстве инертной и гравитационной масс.

Из принципа эквивалентности вытекает, что все явления, обусловленные неинерциальностью системы отсчета, могут наблюдаться в инерциальной системе в результате действия сил тяготения. В качестве примера рассмотрим движение в вакууме световой частицы фотона. Из оптики известно, что в вакууме в отсутствие каких-либо полей световые лучи прямолинейны. Следовательно, в инерциальной системе отсчета в отсутствие гравитационного поля фотон летит со скоростью c по прямолинейной траектории. Примем эту траекторию за ось X. В неинерциальной системе отсчета, движущейся с ускорением – a, фотон будет обладать ускорением a, перпендикулярным оси X. Поэтому относительно неинерциальной системы отсчета одновременно с движением вдоль оси X со скоростью c, фотон будет двигаться равноускорено вдоль оси Y с ускорением, равным а. За время t фотон пройдет вдоль оси X путь x = ct и вдоль оси Y путь y = at²/2. Исключив из этих формул время t, получим уравнение траектории фотона, т.е. в уравнение луча в неинерциальной системе отсчета, в виде параболы

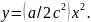
Следовательно, световой луч, прямолинейный в инерциальной системе отсчета, в неинерциальной системе отсчета искривляется и приобретает форму параболы. Согласно принципу эквивалентности, такое же искривление луча должно наблюдаться в инерциальной системе отсчета под действием перпендикулярного к лучу гравитационного поля. Отсюда заключаем, что световые частицы – фотоны подвержены действию сил тяготения. Это искривление луча в поле сил тяготения имеет надежное экспериментальное подтверждение.

Таким образом, поле тяготения (гравитационное поле) может быть «устранено» переходом в систему отсчета, движущуюся с ускорением. На основании этого своеобразного свойства поля тяготения Эйнштейн выдвинул предположение, что гравитация – это не поле, а свойство пространства. Массивное тело не создает вокруг себя никакого поля, оно искривляет вокруг себя пространство. В результате движения тел происходит в искривленном пространстве. И если на тело не действуют силы , то оно покоится либо движется в соответствии с законом инерции. Он выдвинул предположение, что в поле тяготения искривляется не световой луч, а пространство вблизи тяжелой массы. По Эйнштейну, материя как-то искривляет пространство, и другая материя должна двигаться в таком пространстве» естественно» – так, как мы это наблюдаем. Эйнштейн предположил, что наиболее естественным был бы кратчайший путь между двумя заданными точками пространства. В математике соответствующая линия называется геодезической линией. Иными словами, тяжелая масса искривляет пространство вокруг себя, и другие тела движутся в нем по геодезическим линиям. В отношении, например, Солнечной системы геодезические линии кажутся нам эллиптическими орбитами, но в искривленном пространстве они представляют собой прямые линии. Путь тела, движущегося по инерции в искривленном пространстве, описывается не прямой линией, а геодезической линией, форма которой зависит от степени кривизны пространства.

Итак, причина тяготения, его механизм – в свойствах пространства. Пространство – не пассивная арена для физических процессов, структура пространства не постоянна, его свойства изменяются в соответствии с распределением и движением в нем материи. Наличие в пространстве больших масс материи приводит к изменению его свойств. Принципиально меняется описание явления гравитации. По Ньютону, это движение под действием силы (тяготения), по Эйнштейну, это свободное движение тел в искривленном пространстве-времени.

Наглядно представить себе искривленное пространство мы не можем. Мы можем только прибегнуть к аналогии, рассмотрев двумерную поверхность в трехмерном пространстве. Представим себе туго натянутую тонкую резиновую пленку, в центр которой положен тяжелый шар. Под действием его веса пленка изогнется так же, как искривляется пространство вблизи тяжелой массы. Маленький шарик, положенный вблизи большого, скатится к нему как бы под действием силы притяжения. Движение будет происходить по кривой линии (по кратчайшему пути), которая в данном случае будет являться геодезической линией.

Как уже отмечалось, если в уравнение основного закона динамики ввести силы инерции, то второй закон динамики не изменит своего вида, а неинерциальная система отсчета будет неотличима от инерциальной. Чтобы выяснить, к чему приводит переход от инерциальных систем отсчета к неинерциальным в теории относительности, рассмотрим опять круглую платформу радиуса R, которая может вращаться вокруг оси, перпендикулярной ее плоскости и проходящей через центр платформы (ось Z). Предположим сначала, что платформа неподвижна. С помощью масштабной линейки, имеющей длину l, сделаем на периферии платформы и одном из его радиусов отметки на равном расстоянии l одна от другой. Отношение чисел отметок на периферии и по радиусу при малом l будет близко к

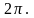
Пусть теперь платформа начинает равномерно вращаться вокруг оси с угловой скоростью и наблюдатель, находящийся на платформе, своей прежней масштабной линейкой производит те же измерения длины окружности платформы и ее радиуса. Приложив линейку вдоль радиуса он обнаружит, что она укладывается столько же раз, сколько и в случае неподвижной платформы. При измерении же длины окружности платформы наблюдатель обнаружит, что линейка укладывается вдоль платформы большее число раз, чем в том случае, когда платформа неподвижна. Произойдет это вследствие лоренцевого сокращения длины линейки, если она направлена вдоль движения. Так как лоренцево сокращение определяется величиной 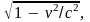где – скорость платформы, то наблюдатель, находящийся на вращающейся платформе, придет к выводу, что отношение длины окружности (периферии платформы) к ее радиусу равно не 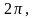как было в случае покоящейся платформы, а равно т.е меньше Поскольку вращающаяся платформа представляет собой неинерциальную систему отсчета, то мы должны сделать вывод, что в неинерциальной системе отсчета пространство не является евклидовым

Но неинерциальные системы, как уже отмечалось, эквивалентны некоторым гравитационным полям. Следовательно, в гравитационном поле пространство перестает быть евклидовым, оно искривлено. Это значит, что геометрические свойства пространства не могут быть чем-то абсолютным даже в смысле специальной теории относительности, а должны зависеть от гравитационных полей.

С другой стороны, гравитационные поля создаются материей. Поэтому геометрия пространства должна определяться материей. Это означает, что геометрия пространства теряет свое самостоятельное существование. Но пространство тесно связано с временем, поэтому можно сказать, что не только свойства пространства, но и свойства времени определяются в конечном счете материей – ее характером и структурой, распределением в пространстве и состоянием движения.

Во всем здесь сказанном о пространстве и времени и заключается основная идея общей теории относительности, созданной Эйнштейном в 1915 г.

Общая теория относительности стала новым, чем специальная теория относительности, подтверждением диалектико-материалистического учения о неразрывной связи пространства и времени с движущейся материей. Своеобразно в ОТО и проявление релятивистских эффектов. Согласно ОТО, сокращение длин и замедление времени наблюдается даже в рамках одной и той же системы отсчета, при переходе от одних точек системы к другим Например, во всех точках, расположенных ближе к центру гравитации поле будет интенсивнее. Следствием этого и время в этих точках будет идти медленнее, а длины отрезков короче, чем в точках, более удаленных от указанного центра.