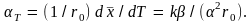8.5. Тепловые свойства твердых тел

8.5.1. Тепловое расширение твердых тел

Почти все твердые тела при нагревании увеличивают свои размеры, исключение составляют кальций, уран и некоторые другие вещества. Это явление называется тепловым расширением. Тепловое расширение можно объяснить исходя из формы кривой зависимости потенциальной энергии взаимодействия атомов от расстояния между ними. Эта кривая воспроизведена на рис. 8.8.

При абсолютном нуле температуры частицы твердого тела (ес-

Рис. 8.8

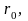ли не учитывать нулевые колебания атомов) располагаются на расстояниях отвечающих минимуму энергии взаимодействия 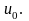Это расстояние определяет размер тела при абсолютном нуле температуры. При некоторой очень низкой температуре частицы начинают колебаться около положений равновесия О. Если повысить температуру тела до значения T₁, частицы будут обладать полной энергией Е₁ и колебаться так, что расстояние между ними будет изменяться от А₁ до В₁ со средним значением О₁. Причем в положении А₁ полная энергия частицы равна энергии отталкивания, а в положении В₁ – энергии притяжения. Из-за различной зависимости сил притяжения и отталкивания между частицами от расстояния между ними (силы отталкивания быстрее убывают с расстоянием, чем силы притяжения), кривая потенциальной энергии несимметрична относительно вертикальной прямой ОО′. Поэтому при движении вправо частица смещается на большее расстояние, чем при движении влево, так что положение равновесия О₁ частицы при температуре Т₁ (середина отрезка А₁В₁) не лежит на прямой ОО′, а смещено вправо. При повышении температуры до Т₂ полная энергия колебаний частиц становится равной Е₂, расстояние между частицами будет изменяться от А₂ до В₂, а положение равновесия О₂ (середина отрезка А₂В₂) сместится вправо относительно положения равновесия О₁, соответствующего температуре Т₁. Таким образом, с ростом температуры возрастает среднее расстояние между частицами тела и его объем увеличивается – тело расширяется. Как видим, тепловое расширение тела обусловлено асимметрией кривой зависимости энергии взаимодействия частиц от расстояния между ними. Если бы эта кривая была симметрична, то точки О, О₁, О₂ и т.д. лежали бы на прямой ОО′ и никакого расширения не было бы. С другой стороны, если бы сила притяжения между частицами изменялась быстрее, чем сила отталкивания (как это и имеет место у кальция, урана и т.д.), то тело бы при нагревании не расширялось, а сжималось.

Найдем теперь аналитическую зависимость среднего расстоя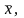ния между частицами тела от температуры Т и коэффициент его теплового расширения 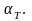Явление теплового расширения показывает, что колебания частиц тела не являются гармоническими, а кривая зависимости потенциальной энергии частицы от величины смещения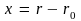 от ее положения равновесия не является параболой с осью ОО′. Чтобы учесть негармоничность колебаний частиц, в разложении потенциальной энергии частиц вблизи положения устойчивого равновесия следует сохранить член, пропорциональный x³:

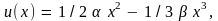
где 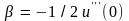– коэффициент ангармоничности межатомной связи. Тогда при смещении частицы вправо (x > 0) член 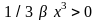вычитается из 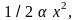а при смещении влево (x < 0) – прибавляется к нему, поэтому левая (от точки О) ветвь кривой 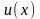идет круче правой. Сила, действующая на частицу, при такой потенциальной энергии

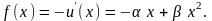
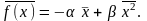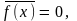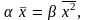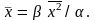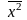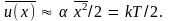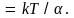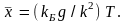Среднее значение силы При свободных колебаниях частицы поэтому откуда Для определения воспользуемся законом равнораспределения энергии по степеням свободы, который в данном случае можно записать в виде Откуда находим Подставляя это значение в выражение для получим Как видим, среднее смещение частицы от положения равновесия пропорционально абсолютной температуре тела. По этой причине и удлинение тела при нагревании будет пропорционально температуре. Коэффициент теплового расширения тела определится как