8.7. Тройная точка. Полиморфные превращения

Как уже говорилось, равновесие двух фаз возможно лишь при вполне определенном соотношении между температурой и давлением; эта зависимость выражается определенной кривой в плоскости рТ. Очевидно, что три фазы одного и того же вещества уже не могут находиться одновременно в равновесии друг с другом вдоль целой линии. Такое равновесие возможно лишь в одной определенной точке на диаграмме рТ, т.е. при вполне определенных значениях давления и температуры. Действительно, в случае равновесия трех фаз (твердой 1, жидкой 2 и газообразной 3) должно выполняться равенство их химических потенциалов:

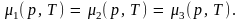
Откуда получаем три уравнения:

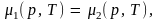
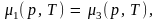
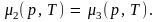
Первое из этих уравнений определяет кривую равновесия твердого тела и жидкости, второе – твердого тела и газа и третье – жидкости и газа. Любая пара из этих уравнений представляет собой систему двух уравнений с двумя неизвестными р и Т. Она имеет решение при вполне определенных значениях этих переменных; обозначим их р_тр и Т_тр. Следовательно, состояние, в котором одновременно сосуществуют три фазы, представляет собой одну точку, называемую тройной точкой. На диаграмме рТ она изображается точкой, являющейся точкой схождения кривых равновесия р = р(Т) каждых двух из трех фаз (рис. 8.12, а). Изображенная на рис. 8.12, а фигура, называется фазовой диаграммой. Области 1, 2, 3 – области трех однородных фаз, разделяющие их линии – кривые равновесия соответствующих двух фаз. Наклон кривой плавления изображен для тела, расширяющегося при плавлении.

Из фазовой диаграммы видно, что твердое вещество, чтобы превратиться в газ при нагревании, не обязательно должно проходить через стадию жидкого состояния. При давлениях ниже тройной точки нагревание твердого тела превращает его непосредственно в пар; такой фазовый переход называется сублимацией (или возгонкой). Кривая равновесия жидкости и газа заканчивается в критической точке (точка К на рис. 8.12, а). Для переходов же между жидкой и твердой фазами существование критической точки невозможно. Поэтому кривая плавления не может просто окончиться и должна продолжаться неограниченно. Кривая равновесия твердого тела с газом уходит в начало координат, т.е. при абсолютном нуле температуры вещество при любом давлении находится в твердом состоянии.

Область твердого состояния не является обычно вся одной и той же фазой. При различных давлениях и температурах вещество может находиться в различных кристаллических состояниях, каждое из которых характеризуется своей определенной кристаллической структурой (полиморфизм). Как и всякие фазы, различные модификации имеют свои области равновесия. Две различные модификации могут находиться в равновесии друг с другом лишь вдоль определенных линий на диаграмме рТ, т.е. при определенной зависимости давления от температуры. Три фазы, например, две кристаллические и одна жидкая, могут находиться в равновесии лишь в определенной тройной точке, т.е. при строго заданных значениях давления и температуры. Таких тройных точек на диаграмме состояния может быть несколько. На рис. 8.12, б в качестве примера схематически изображена фазовая диаграмма серы. Кристаллическая сера может существовать в двух формах. Поэтому на диаграмме состояния имеются две области устойчивости твердого состояния, обозначенные символами 1 и 1^′. Как видим, в этой системе число тройных точек на диаграмме равно трем.

Переход вещества из одной кристаллической модификации в другую называется полиморфным превращением. Он является фазовым переходом первого рода, так как сопровождается поглощением или выделением тепла. Так, превращение α-железа в γ-железо происходит при атмосферном давлении при 910 ⁰С и сопровождается поглощением тепла около 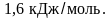При любом фазовом превращении в твердом состоянии происходит перестройка атомной структуры системы, а на это требуется определенное количество теплоты.

При полиморфном превращении часто возникают метастабильные состояния. Это связано с тем, что тепловое движение частиц в кристалле представляет собой малые колебания этих частиц вблизи узлов решетки, совершающиеся с небольшими амплитудами. Из-за малости амплитуд перестройка решетки кристалла при низких температурах затруднена. Она облегчается при повышении температуры. Поэтому при фазовых переходах, связанных с нагреванием вещества, метастабильные состояния возникают редко. При обратных переходах, происходящих при охлаждении вещества, значительно чаще сохраняется высокотемпературная фаза в той области температур, где эта фаза уже неустойчива.

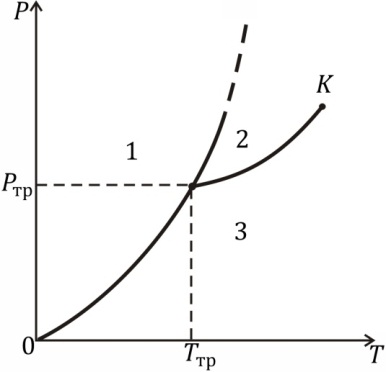
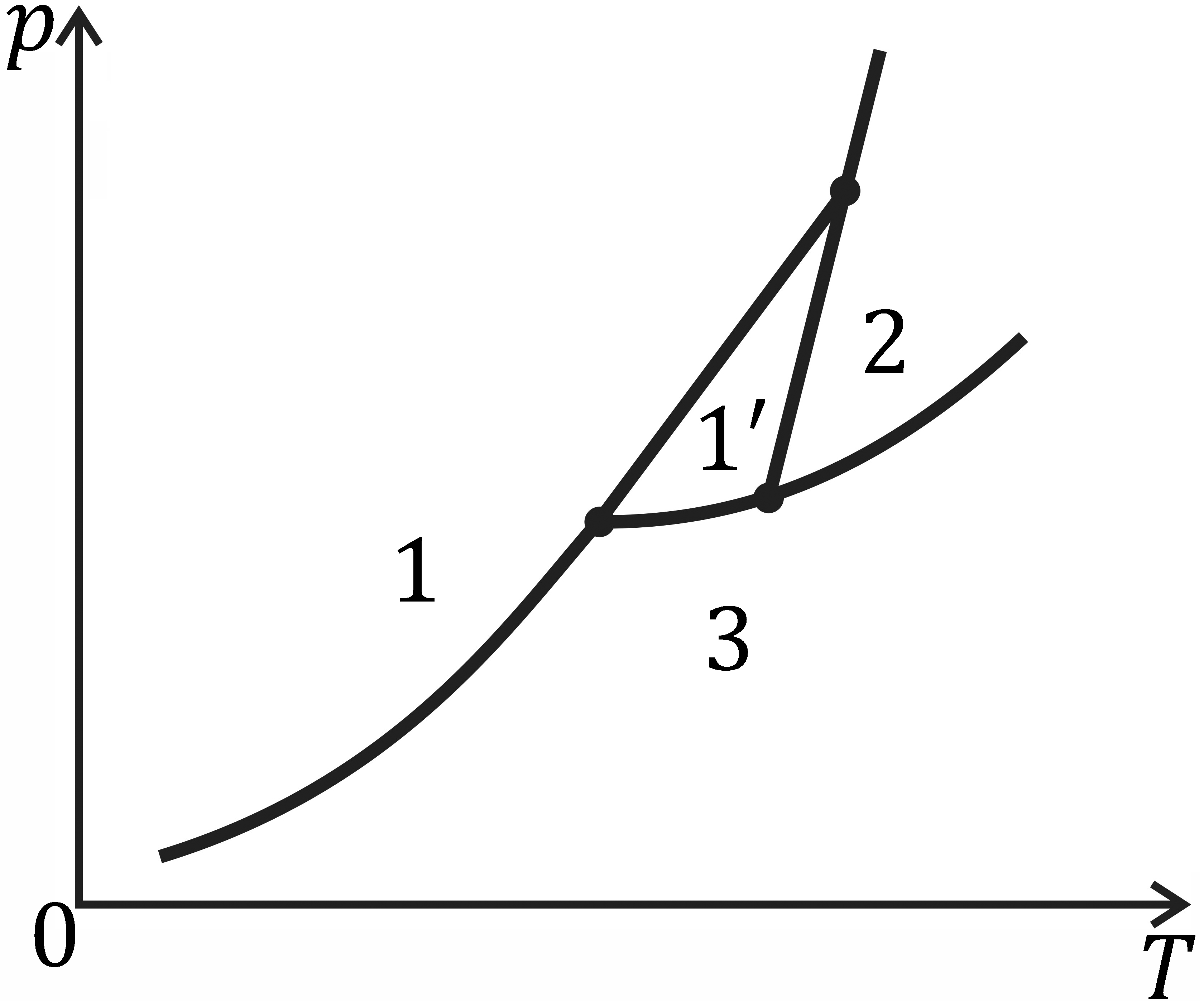
а) б)

Рис. 8.12

Переход между различными кристаллическими модификациями совершается обычно таким образом, что происходит скачкообразная перестройка кристаллической решетки и состояние тела испытывает скачок. Однако наряду с такими скачкообразными переходами возможен и другой тип переходов, связанный с изменением симметрии. Для пояснения этого рассмотрим воображаемый пример. Представим себе тело, которое при низких температурах имеет тетрагональную структуру, т.е. структуру с решеткой, элементарной ячейкой которой служит прямоугольный параллелепипед с квадратным основанием и с высотой с, отличной от ребра основания а, причем Предположим также, что при нагревании тела ребро а удлиняется быстрее высоты с. Тогда при некоторой температуре длины всех сторон сравняются и параллелепипед превратится в куб, изменится симметрия кристалла. Мы получаем по существу другую кристаллическую модификацию.

ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА

1. Астахов А.В. Курс физики. Механика. Кинетическая теория материи. –М.: физматгиз, 1977. -384 с.

2. Базаров И.П. Термодинамика. –М.: Высшая школа, 1991. -376 с.

3. Василевский А.С., Мултановский В.В. Статистическая физика и термодинамика. –М.: Просвещение, 1985. -256 с.

4. Гершензон Е.М., Малов Н.Н., Мансуров А.Н., Эткин В.С. Курс общей физики. Молекулярная физика. –М.: Просвещение, 1982. -208 с.

5. Жданов Г.С., Хунджуа А.Г. Лекции по физике твердого тела. –М.: Изд. МГУ, 1988. -232 с.

6. Кикоин А.К., Кикоин И. К. Молекулярная физика. –М.: Наука, 1976. 176 с.

7. Ландау Л.Д., Ахиезер А.И., Лифшиц Е.М. Курс общей физики. Механика и молекулярная физика. –М.: Наука, 1965. -384 с.

8. Орлов В.А., Никифоров Г.Г. Равновесная и неравновесная термодинамика: Учебное пособие. –М.: БИНОМ. Лаборатория знаний, 2005. -120 с.

9. Пригожин И. От существующего к возникающему. –М.: Изд УРСС научной и учебной литературы, 2002. -288 с.

10. Рейф Ф. Статистическая физика. –М.: Наука, 1977. -324с

11. Румер Ю.Б., Рывкин М.Ш. Термодинамика статистическая физика и кинетика. –М.: Наука, 1977.-551с.

12. Седов Е.А. Одна формула и весь мир. –М.: Знание, 1982.-176 с.

13. Степухович А.Д., Улицкий В.А. Лекции по статистической физике. –М.: Высшая школа, 178.-150 с.

14. Стратонович Р.Л., Полякова М.С. Элементы молекулярной физики, термодинамики и статистической физики. –М.: изд. МГУ, 1981. -176 с.

15. Сущинский М.М. Курс физики, т. 1. -М.: Наука, 1973.

-352 с.

16. Тер Хаар Д., Вегеланд Г. Элементарная термодинамика. –М.: Мир,1968. -220 с.

17. Хуанг К. Статистическая механика. –М.: Мир, 1966.

-520 с.

18. Шебалин О.Д. Молекулярная физика. –М.: Высшая школа, 1978. -168 с.

233