7.9. Роль поверхностных эффектов в явлении

конденсации

Как уже отмечалось, при изотермическом сжатии газа, в некоторой точке 1, показанной на pV- диаграмме на рис. 7.3, должна начаться его конденсация. При дальнейшем сжатии давление в системе должно оставаться постоянным. В действительности же давление иногда продолжает расти вдоль кривой 1–2. Однако состояния системы на этой кривой не являются стабильными. Задержка в конденсации объясняется поверхностными эффектами, т.е. тем, что образование в паре вследствие флуктуаций зародышей (капель жидкости) малых размеров жидкой фазы из-за поверхностной свободной энергии этих зародышей приводит к увеличению свободной энергии системы, и поэтому фазовый переход оказывается термодинамически невыгодным. Конденсация начинается, когда образуются капли жидкости некоторых критических размеров, начиная с которых они будут расти. Найдем этот критический размер зародыша.

Предположим, что в результате происшедшей флуктуации в паре при температуре Т и давлении р образовалась капелька жидкости радиуса R. Потенциал Гиббса пара до образования капли равен

G₀ = = μ₂(p, T)N,

где μ₂ – химический потенциал пара, N – число частиц пара. После образования капли потенциал Гиббса системы с учетом поверхностной энергии будет

G = F + pV = N₁f₁ + N₂f₂ + σS + p(N₁v₁ + N₂v₂) = N₁(f₁ + pv₁) +

+ N₂(f₂ + pv₂) + = N₁μ₁ + N₂μ₂ + ,

где N₂ – число частиц пара, N₁ – число частиц в капле (N₁ + N₂ =

Рис. 7.11

= N), v₁ и v₂ – удельные объемы жидкой и газообразной фаз, f₁ и f₂ – их свободные энергии в расчете на одну частицу, σ – коэффициент поверхностного натяжения, S – площадь поверхности капли. Изменение потенциала Гиббса при образовании в парообразной фазе капли жидкости равно

∆G = G – G₀ =

= (μ₁ – μ₂)N₁ + σS.

Выразив N₁ и S через радиус капли, получим С учетом этого будем иметь

(7.8)

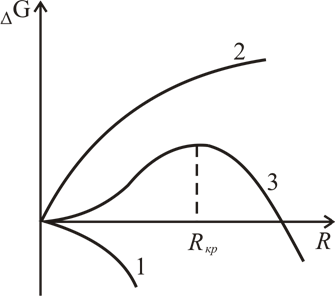
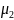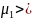
Возможны два случая: 1) ; 2) . На рис. 7.11 приведена зависимость ΔG от радиуса капли R для случая < . Кривая 1 соответствует первому члену в правой части равенства (7.8), а кривая 2 – второму члену. Суммарная кривая _{3 дает зависимость изменения термодинамического потенциала системы от размера зародыша. В случае, когда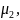} новая фаза (жидкость) имеет при заданных р и Т химический потенциал больший, чем старая (пар), и является менее устойчивой. Появление капельки жидкости в паре при всех ее размерах R ведет к росту ∆G, поэтому образование новой фазы всегда термодинамически невыгодно.

Рис. 7.12

Если в результате флуктуации и образуется капля в таком паре, то каких бы размеров она ни была, она обязательно быстро исчезнет. Во втором случае, изображенном на рис. 7.11, с увеличением размера возникшей флуктуации второй фазы величина ∆G вначале растет, при некотором R = R_кр достигает максимального значения и затем убывает. Это означает, что малые флуктуации новой фазы являются неустойчивыми. Однако при больших образованиях второй фазы, когда R > R_кр, новая фаза становится более устойчивой. Величина R_кр представляет собой критический радиус зародыша (капли жидкости). Его значение найдем из условия максимума функции

Получим

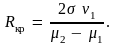
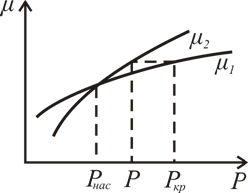
Отсюда видно, что критический радиус зародыша пропорционален коэффициенту поверхностного натяжения. На рис. 7.12 изображена кривая зависимости химического потенциала μ от давления p при T = const для жидкой (кривая ) и газообразной (кривая ) фаз. Абсцисса точки пересечения кривых равна давлению насыщенного пара . Из этого рисунка видно, что разность тем больше, чем больше степень пересыщения пара 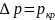– p. Таким образом, чем больше пересыщен пар, тем

1 В твердом теле, как мы увидим далее, могут распространяться помимо продольных вон еще две поперечные волны со взаимно перпендикулярными направлениями колебаний.

196