7.7. Термодинамическое описание фазового перехода пар – жидкость

Получим теперь термодинамические условия фазового перехода и фазового равновесия жидкости и пара. Пусть имеем две фазы вещества: жидкое (1) и газообразное (2). Термодинамический потенциал Гиббса такой двухфазной системы будет , где 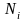– число частиц в i-ой фазе (i = 1,2), а μ_i – термодинамический потенциал Гиббса, приходящийся на одну частицу i-ой фазы; эта величина характеризует внутренние свойства фазы и представляет собой ее химический потенциал.

Если две фазы не находятся в равновесии друг с другом, то число частиц в обеих фазах будет изменяться. При изменении числа частиц в первой фазе на 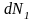, а во второй на термодинамический потенциал системы изменится на 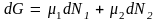. Но так как 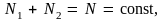то 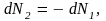и тогда Поскольку система не находится в равновесии, то ее термодинамический потенциал будет уменьшаться: Отсюда следует, что если то а 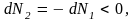т.е. число частиц в первой фазе возрастает, а во второй уменьшается. Это означает, что переход вещества происходит из второй фазы в первую, т.е. имеет место процесс конденсации. Процесс будет продолжаться до тех пор пока все вещество не окажется в фазе 1, т.е. пока пар полностью не сконденсируется. В этом случае термодинамический потенциал достигнет минимального значения 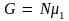. Отсюда следует, что при 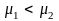термодинамически устойчивой будет фаза 1 (жидкость), так как небольшое уменьшение числа частиц в первой фазе и увеличение их во второй вызовет поток частиц из второй фазы в первую. 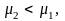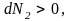Если имеет место неравенство то а 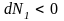. Переход вещества будет происходить из фазы 1 в фазу 2 – парообразование. Термодинамический потенциал достигнет своего минимального значения 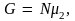когда все вещество перейдет в парообразное состояние; термодинамически устойчивой будет фаза 2 (пар).

Поскольку химический потенциал, как и термодинамический потенциал Гиббса, является функцией температуры Т и давления р, то выполнение того или иного неравенства потенциалов фаз определяется значениями температуры и давления: при одних значениях Т и р меньшим окажется химический потенциал жидкости, а при других – пара. Это означает, что при одних значениях температуры и давления устойчивой будет жидкая фаза, а при других – газообразная. Если температура и давление таковы, что то выполняется условие минимума термодинамического потенциала 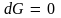– двухфазная система (жидкость + пар) будет находиться в равновесии. В этом случае 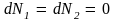– переход вещества из одной фазы в другую не происходит. Имеет место равновесие фаз между собой. Таким образом, условием равновесия двух фаз является равенство их химических потенциалов:

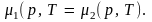(7.5)

При этом температуры и давления фаз также равны друг другу:

Т₁ = Т₂ = Т, р₁ = р₂ = р,

где .Т и р – температура и давление фазового равновесия и перехода.

Учитывая определение химического потенциала, перепишем равенство (7.5) в виде

где u, s, v – удельная (в расчете на одну молекулу) внутренняя энергия, энтропия и объем фаз соответственно. Откуда

u₂ – u₁ + p(v₂ – v₁) = T(s₂ – s₁)

или

∆u + p∆v = T∆s.

Согласно первому закону термодинамики, левая часть этого равенства есть удельная теплота фазового перехода q. Следовательно,

q = T(s₂ – s₁).

Отсюда видно, что если энтропия конечной фазы больше энтропии начальной фазы, т.е. s₂ > s₁, то q > 0 – фазовый переход (парообразование) происходит с поглощением теплоты; если же, наоборот, s₂ < s₁, то q < 0 – фазовый переход (конденсация) происходит с выделением теплоты. Превращения вещества из одной фазы в другую, связанные с поглощением или выделением теплоты, называются фазовыми переходами первого рода. Существуют фазовые переходы и второго рода, которые не сопровождаются поглощением или выделением тепла.