6.5.1 Випадок непов’язаних(незалежних) вибірок
Нехай
є дві незалежні
вибірки
та
,
які взято з нормальної сукупності з
дисперсіями
та
.
Перевірить нульову гіпотезу
,
де
й
- математичні сподівання відповідних
генеральних сукупностей.
1 випадок:
Тому
що
,
апріорі, як правило, невідомі, то перш
ніж перевірять гіпотезу
з початку перевіряють гіпотезу про
рівність дисперсій
,
якщо ця гіпотеза не відкинута, тоді
переходимо до перевірки гіпотези:
.
Критерій:
,
де
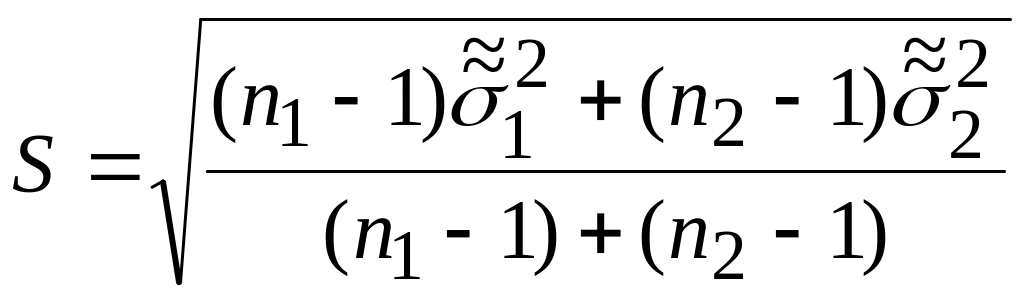, (7.0)
-розподілення
Стьюдента з
ступенів свободи. Критична область –
двостороння.
Якщо , то гіпотезу відкидають.
2
випадок.
Дисперсії
,
усе так як у першому випадку, але
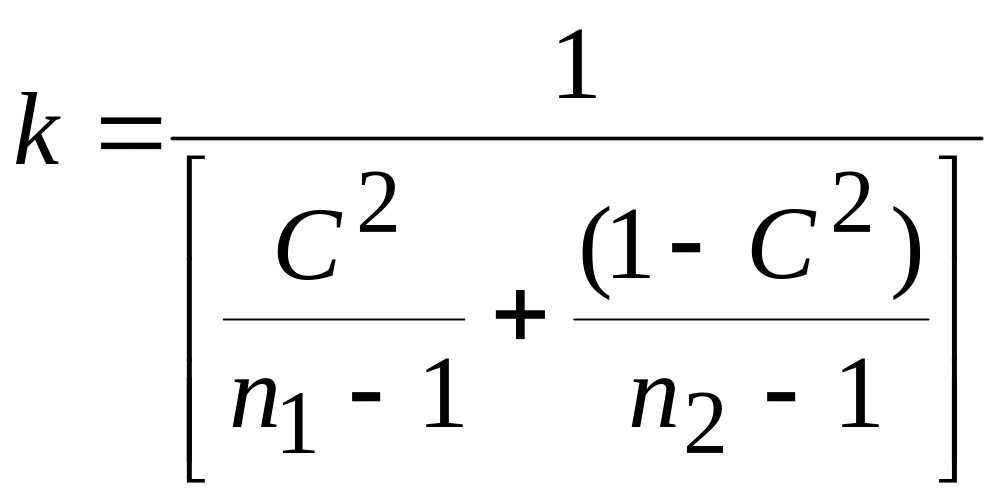, де
.
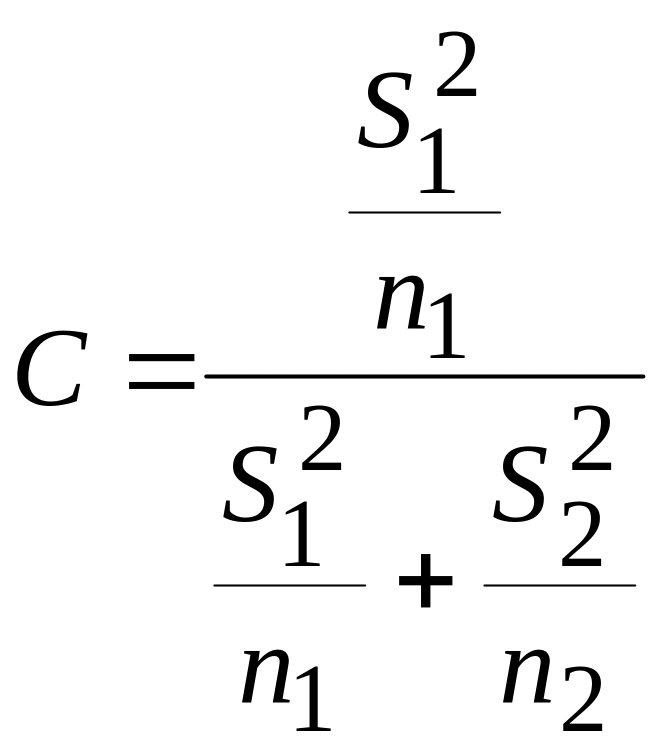6.5.2 Випадок пов’язаних(залежних) вибірок[2,3]
Нехай
дві генеральні сукупності
та
розподілені нормально, при чому
і невідомі. Маємо дві пов’язані(залежні)
вибірки
,
відповідно з першої та другої генеральної
сукупності.
Нульову та альтернативну гіпотези можна сформулювати відповідно як
,
або
.
Введемо
величину
,
.
Тоді
,
-
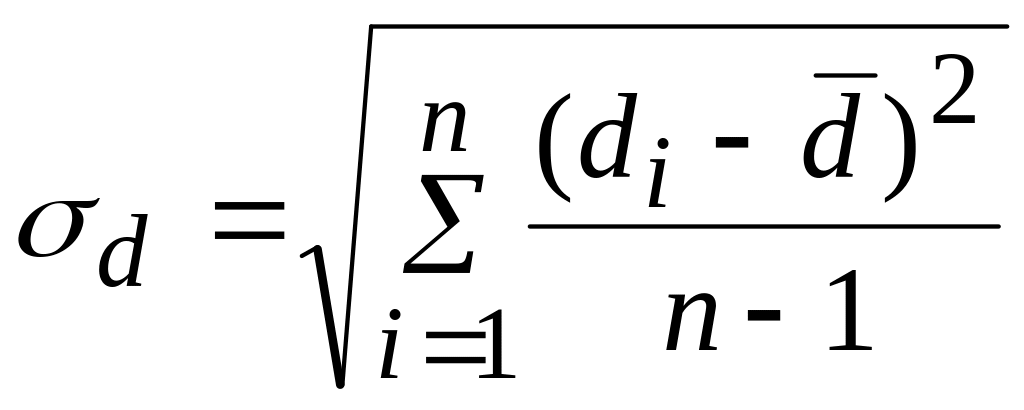стандартне відхилення
значень різниць
.
,
.
Таким
чином, спостережуване значення
статистичного критерію обчислюється
за формулою
.
За
таблицею критичних точок розподілу
Стьюдента знаходимо двостороннє критичне
значення
.
Якщо
- немає підстав відхилити
.
Якщо
-
відхиляється.
6.6 Стійкість (робастність) критеріїв* [1]
При
використанні розглянутих вище
параметричних критеріїв Стьюдента,
,
та
критерія
Фішера, повинна виконуватись умова
нормального розподілу вибіркових даних.
При порушенні цієї вимоги одні критерії
зберігають свою працездатність,
тобто,
ймовірності
та
при їх використанні залишаються майже
такими, я к і при нормальному розподілі,
а інші її втрачають.
Визначення 37. Критерії, що зберігають свою працездатність при порушенні вимоги нормального розподілу вибіркових даних називаються робастними (стійкими).
Зауваження. Непараметричні критерії (Колмогорова-Смірнова, Вілкоксона та ін.) мають більшу стійкість, натомість, їх потужність менше,ніж у параметричних. У той же час параметричні критерії (Стьюдента, , та критерій) мають більшу потужність, але не є робастними. Таким чином, доцільне використання одночасно низки як параметричних, так і непараметричних критеріїв при вирішенні певної задачі, якщо це можливо. Саме такий підхід реалізовано в програмних універсальних статистичних пакетах.
Зауваження. Часто має місце ситуація, коли один і той же критерій є стійкім при перевірці певної нульової гіпотези і не є стійким при перевірці іншої. Типовий приклад: критерій при перевірці нульової гіпотези щодо законів розподілу є робастним, тобто веде себе як непараметричний, а при перевірці гіпотези щодо дисперсії випадкової величини, яка вивчається, він не є стійким. Тому коректніше говорити не про робастність певного статистичного критерію, а про робастність певної статистичної процедури (критерій+гіпотеза, що перевіряється).
Розглянемо робастність кожного з наведених вище параметричних критеріїв.