3.3.4 Випадок логарифмічно нормального розподілу [7]
Логарифмування
є одним з тривіальних функціональних
перетворень вибіркових значень
у випадку, коли має місце порушення
передумови щодо їх нормальності. Вимога
нормального закону вибіркових значень
виникає всяк раз, коли постає мова про
коректне застосування параметричних
критеріїв згоди при перевірці статистичних
гіпотез, зокрема, у дисперсійному,
кореляційному та регресійному аналізі
(див. нижче). Логарифмування застосовується
у тих випадках, коли
,
.
Тобто, випадкова величина
має нормальний закон розподілу.
Враховуючи, що
,
а оцінка центру розподілу
,
отримаємо оцінку середнього значення
величини
:
; (1)
Інтервальна оцінка для центру розподілу величини має вигляд
. (2)
З (2) з у рахуванням (1) отримаємо інтервальну оцінку для медіани, як центру розподілу:
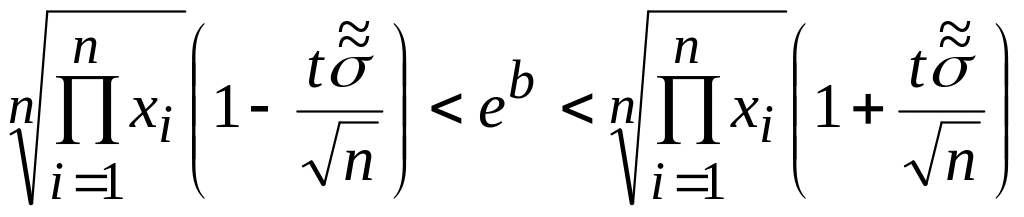. (3)
3.3.5 Випадок довільного розподілу
Нехай - довільна вибірка. При великих можна побудувати прості довірчі інтервали за умови припущення щодо нормальності на підставі ЦГТ, згідно з якою розподілення величини:
.
Якщо
-
обґрунтована оцінка
,
тоді розподілення величини
і отже
;
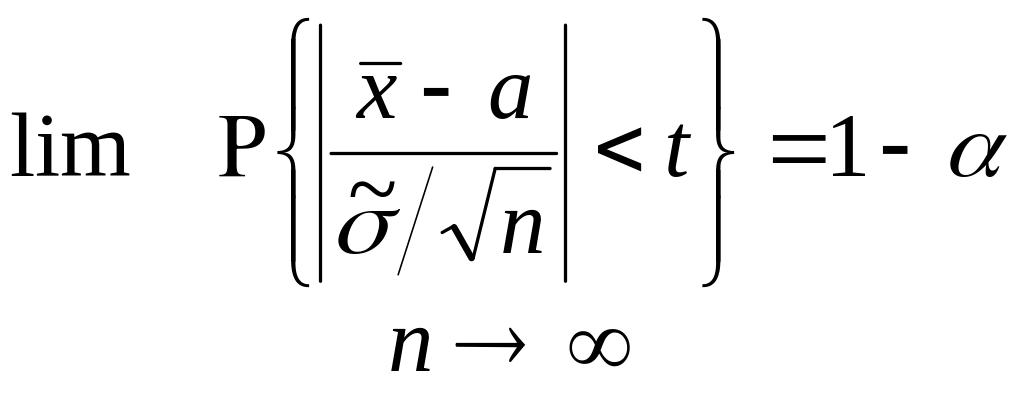або
,
при
.
(*)
На підставі (*) розглянемо два часткових випадки.
Оцінка параметру розподілення Пуассона
Нехай
- незалежні ВВ, що мають розподілення
Пуассона з параметром
.
Тоді
,
-
обґрунтована оцінка параметру
,
при
.
;
.
Оцінка
параметру
в розподілі Бернуллі
Нехай
-
число успіхів в
іспитах Бернуллі з ймовірністю успіху
в кожному іспиті дорівнює
.
Величина
- незсунена і обґрунтована оцінка
параметра
.
Звідси при
;
де
.
Тоді
;
.
I. Доповнення до параграфу про точкову оцінку параметрів розподілу
Згідно з [8]:
-
обґрунтована, але зміщена оцінка СКВ
при
.
Незміщена і обґрунтована оцінка параметра нормального розподілення:
, (**)
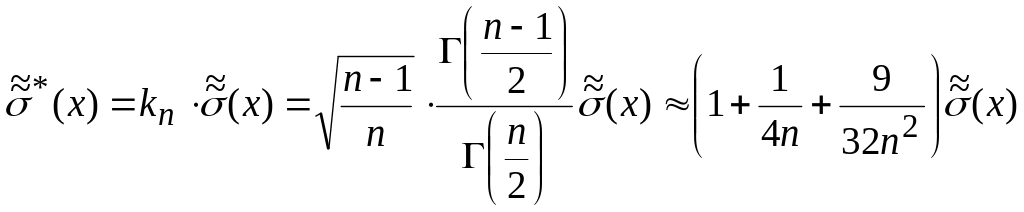де
-
гамма-функція.
Значення
для
приведені в таблиці:
|
4 |
5 |
6 |
7 |
8 |
9 |
|||||
|
1.085 |
1.064 |
1.051 |
1.042 |
1.036 |
1.032 |
|||||
При
застосовується права частина формули
(**).
II. Побудова довірчого інтервалу до параметру Пуасонівського розподілу[9]
Для точних інтервалів користаються тим фактом, що функція розподілу за законом Пуассона виражається у термінах - розподілу. А саме, наступна формула (стор.160):
; (***)
Довірчий інтервал.
Використовуючи
(***) отримуємо довірчі інтервали для
:
Для
:
; (1*)
Так як
;
тоді
де
-
квантіль рівня
,
-
розподілення з
ступенями свободи.
Аналогічно
знаходимо
:
;
;
.
Приклад. Якщо на літаку, що залишає складальній цех, не вистачає однієї заклепки і якщо можливо представити, що кількість заклепок, яких не вистачає, на одному літаку розподілена за законом Пуассона, тоді 99%-ий довірчий інтервал для невідомого параметру ( тобто для середнього числа відсутніх заклепок на один літак у всій партії літаків)суть:
;
.
Д/З
1. Для
2.
Побудувати довірчий інтервал з [1] для
Порівняти результати.
Література
1. Чистяков В.П. Курс теории вероятностей – 2-е издание, переработанное и дополненное - М.: Наука. Главная редакция физико– математической литературы, 1982 г.-256 стр.
2. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие для вузов. Издание 5-е, переработанное и дополненное М., „Вища школа”,1977г.- 497стр.
3.Айвазян С.А. и др. Прикладная статистика: Основы моделирования и первичная обработка данных. Справочное издательство /С.А.Айвазян, Н.С. Енюков, Л.Д. Мешалкин, - М.:Финансы та статистика, 1983 г.-471стр.
4. Справочник по теории вероятностей и математической статистике/ В.С. Коронюк, Н.І. Портенко, А.В. Скороход, А.Ф. Турбин, -М.: Наука. Главная редакция физико–математической литературы, 1985 г.-640 стр.
5.Турчин В.Н., Дрожжина А.В. Лабораторный практикум для курса “Теория вероятностей и математичская статистика”. Днепропетровск, Ротапринт ДГУ., 1987 г.
6. Чернова Н. І. Краткий конспект лекций по математической статистике. Новосибірськ.,1997 г.
7. Румшиский Л. З. Математическая обработка результатов эксперимента. Главная ред. физико-матем. изд-ва «Наука», 1971.
8. Справочник по вероятностным расчетам. Воениздат, 1970; 536 стр.; Г.Г.Абезгауз, А.П.Тронь, Ю.Н.Копенкин, І.А.Коровина, стр.291-292.
9. К.А.Браунли: Статистическая теория и методы в науке и технике. К.А.Браунли: перевод с английського М.С. Никулина, под редакцией Л.Н.Большик. Главная редакция физико-математической литературы издательства “Наука”,1977 г. стр.160.
10. А. М. Дубров. Обработка статистических данных методом главных компонент. М., «Статистика», 1978.