3.2.5. Оцінка параметра експоненціального розподілу

,

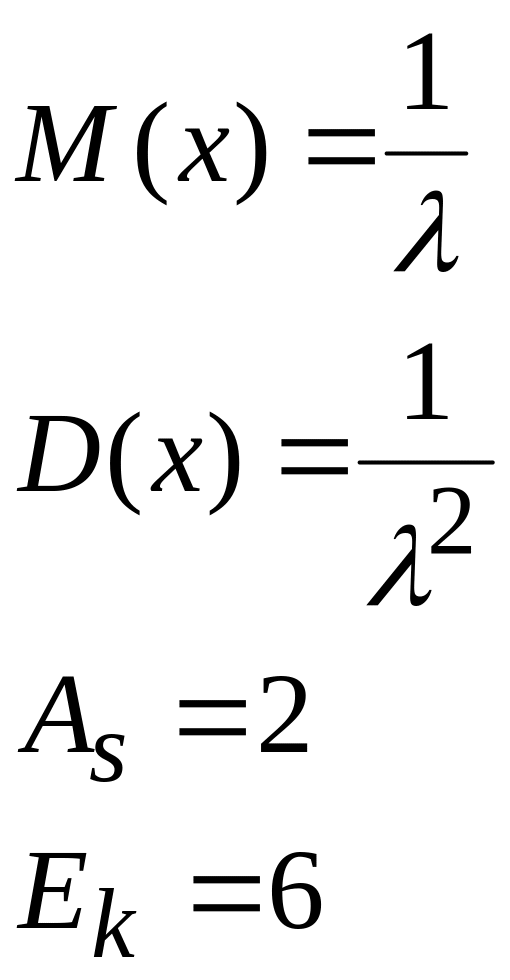
Примітка. Параметри реальних ознак, що мають такі розподіли:

1. Час між збоями технічного пристрою.

2. Довговічність виробу, що працює в режимі експлуатації.

3.2.6. Оцінка параметрів розподілу Коші

Числових характеристик не існує.

Метод прирівнювання теоретичних та емпіричних квантилів дозволяє отримати такі оцінки:

; […] - ціла частина числа.

- вибіркова медіана.

.

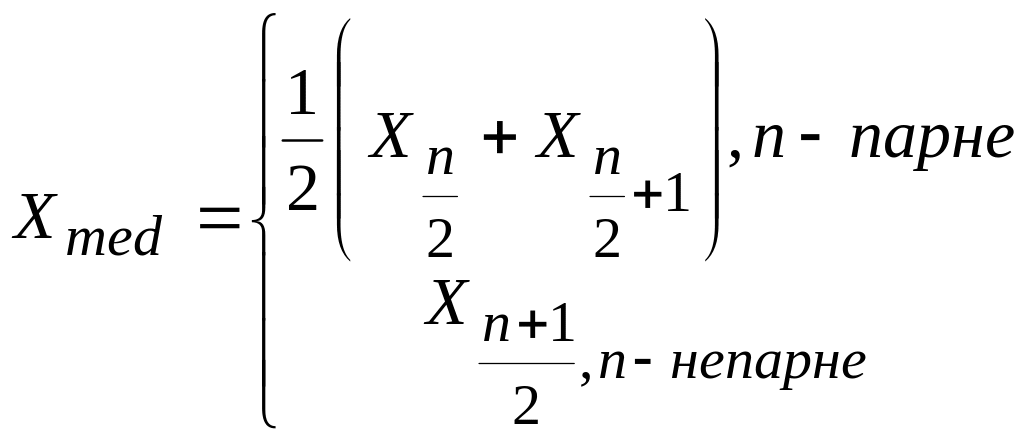- вибірковий квантиль рівня 0,75, тобто, -ий член варіаційного ряду, побудованого за наявною вибіркою.

3.2.7. Оцінка параметрів біноміального розподілу

- число появ події в i-тому, що цікавить нас, спостереженні, тобто в i-тій m-кратній серії незалежних випробувань.

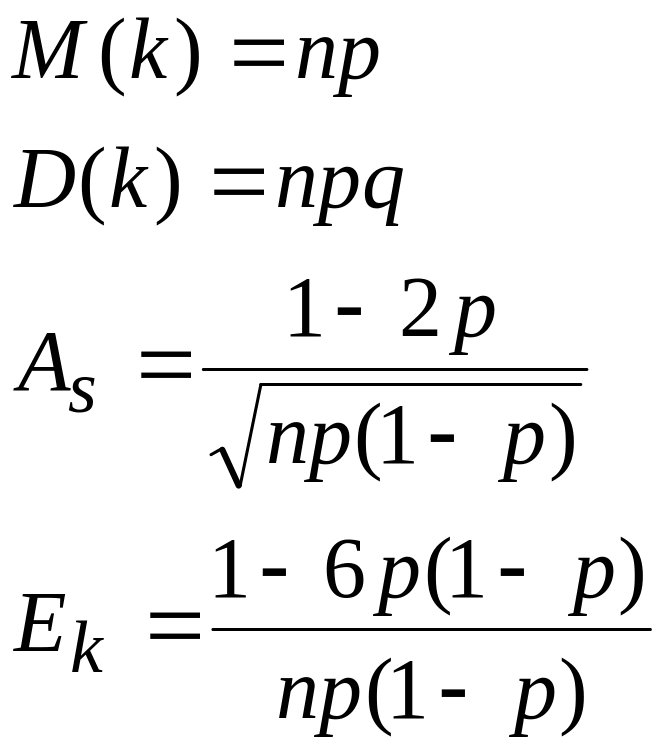
3.2.8. Оцінка параметрів пуассонівського розподілу

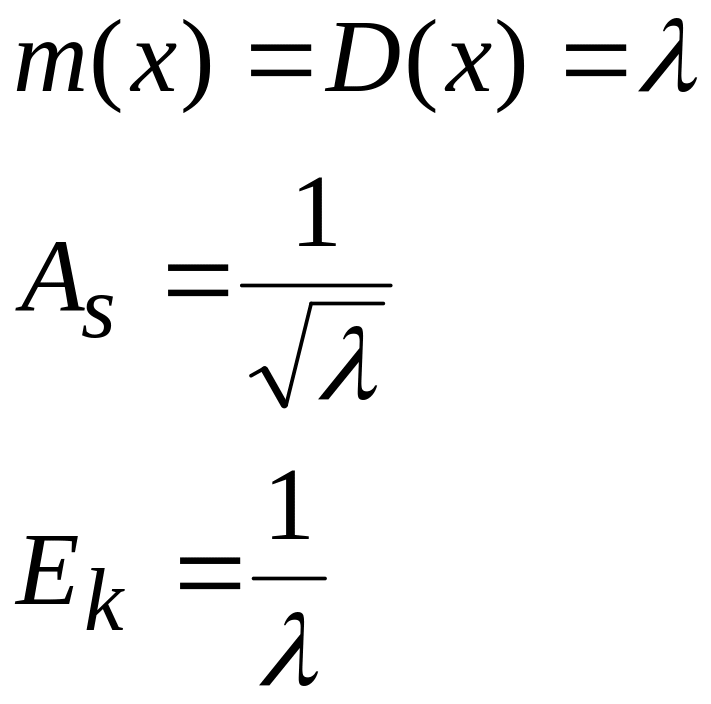
, де - число появ події, що цікавить нас, в проміжок i-тої проконтрольованої одиниці часу.

3.2.9. Оцінка параметрів гіпергеометричного розподілу

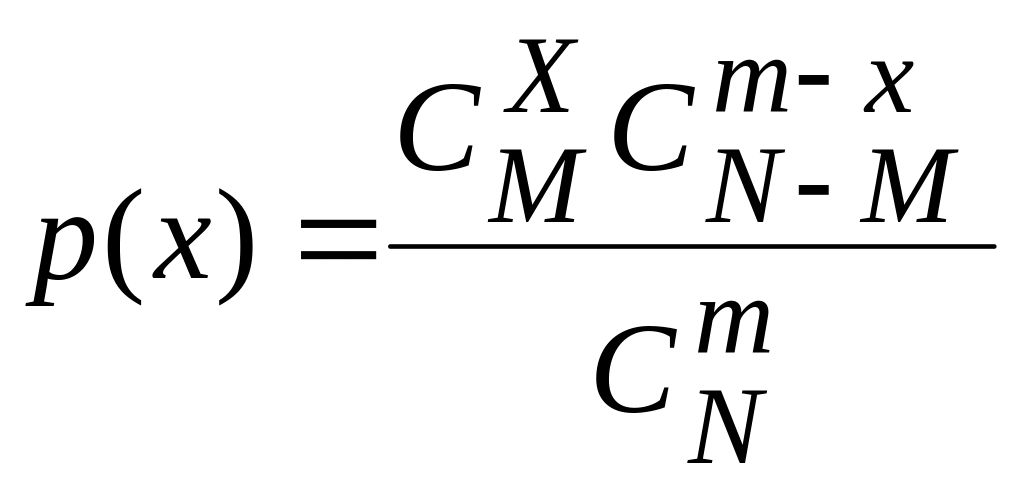
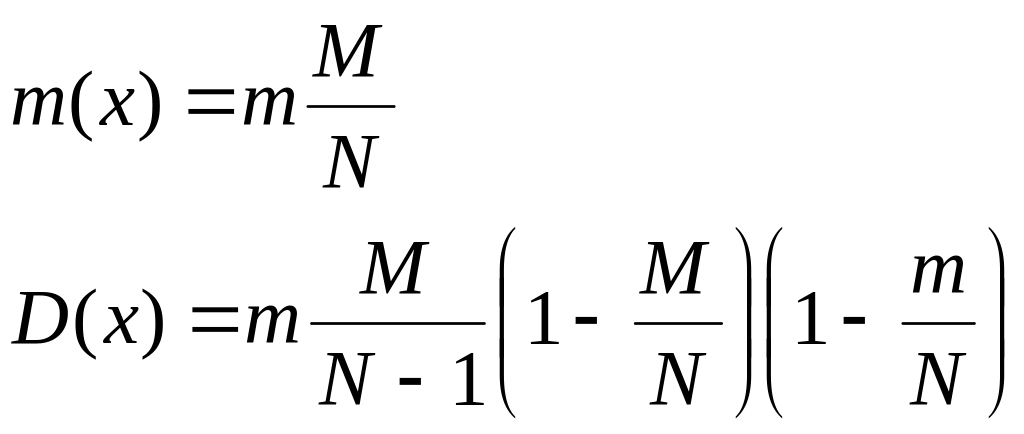
При відомому значенні параметра :

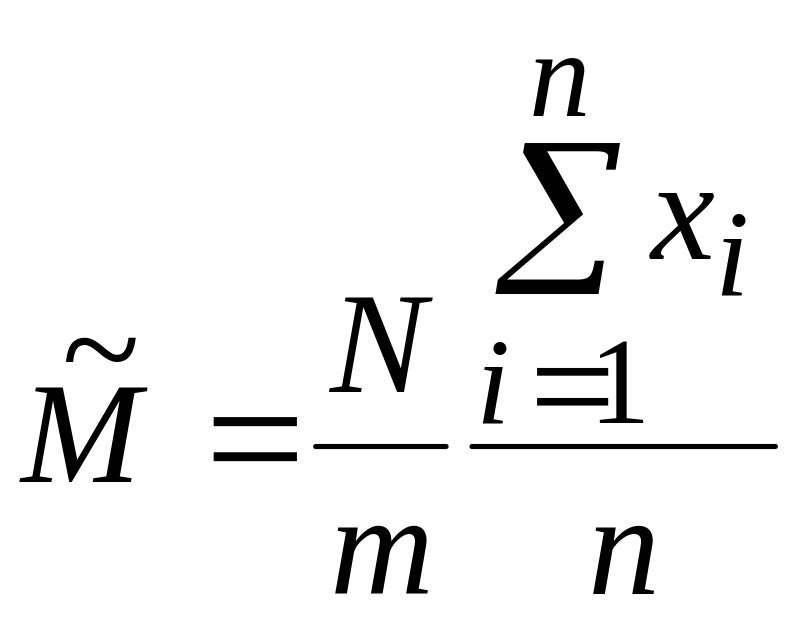, де - зафіксована в i-тому спостереженні кількість об'єктів, що мають задані властивості серед випадкових вилучень із сукупності, що складається з об'єктів.

3.3. Інтервальні оцінки

Визначення 19. Інтервальною називається оцінка, яка визначається двома числами – кінцями інтервалу.

Нехай - оцінка параметра , тобто . Ясно, що чим , тим точніша точкова оцінка . Якщо і , то чим , тим точніша оцінка. Нерівність не здійснюється суворо, а з ймовірністю .

Визначення 20. Надійністю (довірчою ймовірністю) оцінки за називають ймовірність , з якою здійснюється нерівність , тобто

Визначення 21. Вираз називають довірчим інтервалом, який покриває параметр , що оцінюється, з надійністю .

Розглянемо низку важливих теорем, що стосуються точних розподілів, і які лежать в основі підходів для оцінювання параметрів деяких розподілів і перевірки різних статистичних гіпотез.

Теорема 5. Якщо елементи вибірки незалежні і розподілені нормально з параметрами , то і незалежні, причому розподілено нормально з параметрами , а має розподіл з ступенями свободи.

Теорема 6. Якщо елементи вибірки незалежні і кожна з цих величин розподілена нормально з параметрами , то величина має розподіл Стьюдента з ступенями свободи.

Теорема 7. Нехай і - дві незалежні вибірки і будь-яка з цих незалежних величин має нормальний розподіл з параметрами . Тоді величина , де - вибіркова дисперсія вибірки , а - вибіркова дисперсія вибірки , має розподіл з і ступенями свободи відповідно.

3.3.1. Інтервальні оцінки параметрів нормального розподілу

I. Оцінка параметра при відомому

Нехай . Для оцінки природно використовувати згідно з теоремою 5. Для ми можемо знайти таке (квантиль), що .

Але нерівність рівносильна такій:

. ( або задаються наперед)

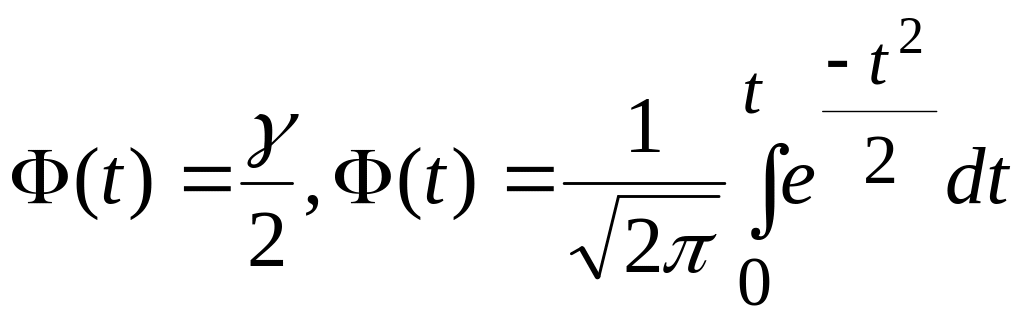- інтегральна функція Лапласа.

II. Оцінка параметру при невідомому

Згідно з теоремою 6 величина розподілена за законом Стьюдента з степенями свободи. Враховуючі, що

, тоді - має розподілення Стьюдента з ступенями свободи. Тому для заданої надійності ми можемо за таблицею розподілення Стюдента знайти межі . Тоді

Рис. 3.1 Критичні області розподілу

III. Оцінка параметру

Нехай . Згідно з теоремою 6 величина . Довірчий інтервал виберемо таким чином, щоб межі і забезпечили виконання умови (рис. 1);

;

;

;

;

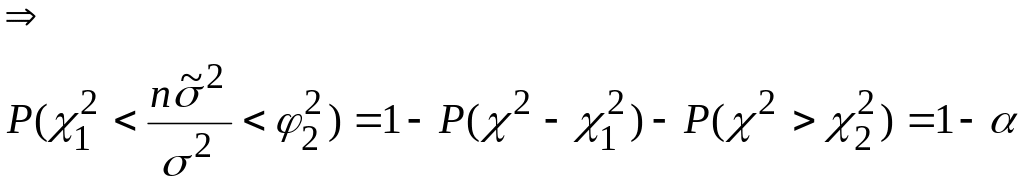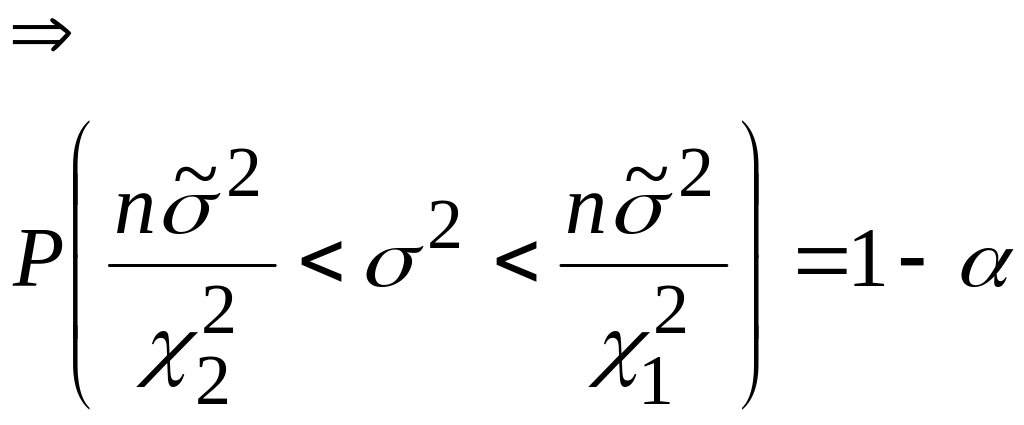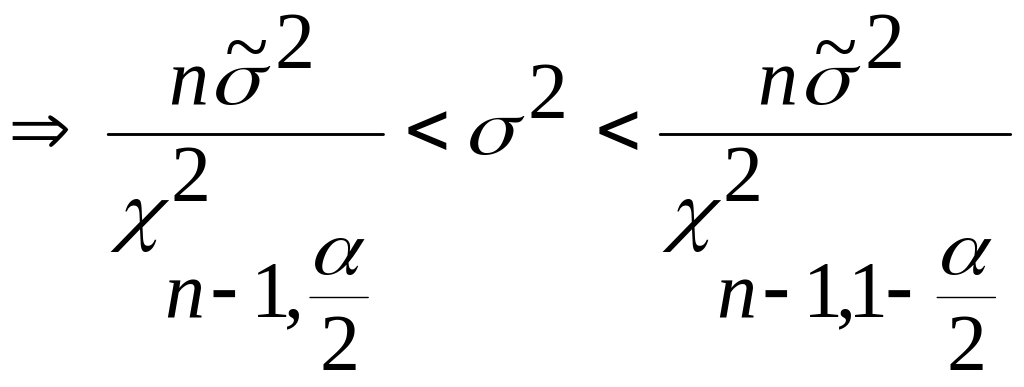
3.3.2 Оцінка параметру експоненціального розподілення

Існує теорема про те, що має розподіл з ступенями свободи. Згідно з цим ж законом величина . Тоді інтервал оцінки може бути визначена за співвідношенням

Для визначення та використовуємо співвідношення ;

, де , - будь-які позитивні числа, менші за одиницю, причому . Тоді

;

.

;

.

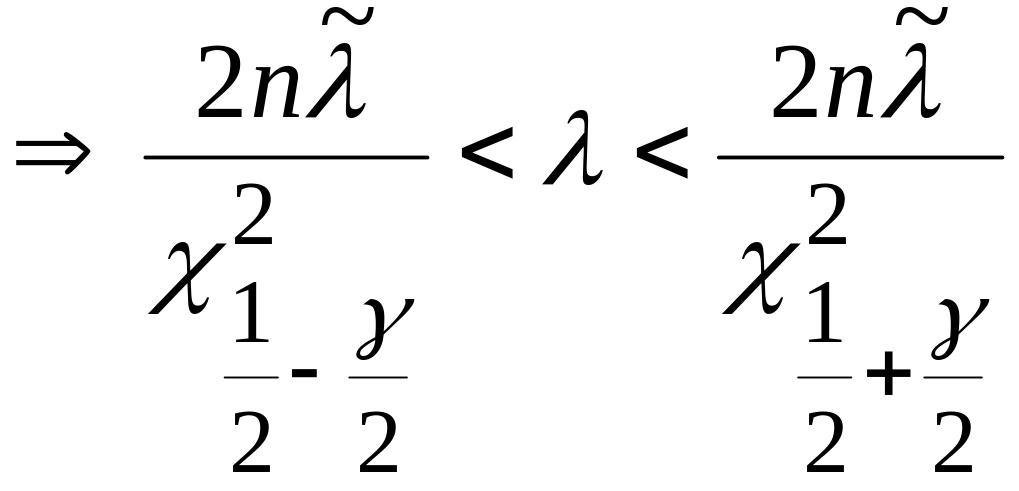3.3.3 Випадок рівномірного розподілу на відрізку з фіксованим кінцем

Нехай - вибірка випадкової величини з невідомим параметром . Нехай , при . Оцінка - обґрунтована, але зміщена. Незміщеною буде оцінка . Вона є ефективна.

Розподілення величини не залежить від 0 і має вигляд:

За заданим виберемо таке, щоб .Звідси знайдемо: . Тоді .