10, 15. Проблемы параллельной обработки данных.

Проблемы параллельного программирования:

• Разработка параллельных алгоритмов, которые существенно сложнее обычных последовательных. Как правило, даже разрабатывают сначала последовательный алгоритм, а затем адаптирую к параллельному варианту.

• Оценка эффективности параллельных алгоритмов. Существуют специальные программы, которые на каждом этапе предсказывают возможную эффективность.

• Существуют проблемы синхронизации и проблемы взаимных блокировок.

Параллельную модель программирования характеризуют:

• возможность добиться более высокой производительности;

• применение специальных приемов и инструментов программирования;

• повышенная трудоемкость программирования;

• проблемы с переносимостью программ.

Требования к параллельным программам:

• достаточная степень параллелизма;

• хорошая масштабируемость;

• детерминизм;

• эффективность.

Повышенная трудоёмкость параллельного программирования связана с тем, что программист

должен заботиться:

• об управлении работой множества процессов;

• об организации межпроцессных пересылок данных;

• о вероятности тупиковых ситуаций (взаимных блокировках);

• о нелокальном и динамическом характере ошибок;

• о возможной утрате детерминизма («гонки за данными»);

• о масштабируемости;

• о сбалансированной загрузке вычислительных узлов.

10. Метод параллелепипедов.

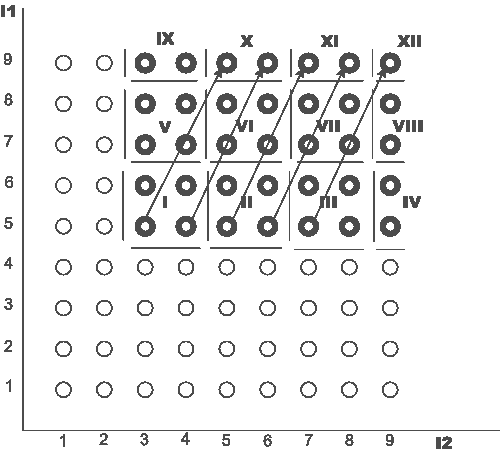В этом методе подмножества независимо выполняемых операций ищутся в форме прямоугольных параллелепипедов. Данный метод так же применим и для простых циклов.

ПРИМЕР:

DO 2 I=1,15

X(I)=X(G*I-27)

2 CONTINUE

В этом примере рассматривается одномерный случай пространства итераций, и в результате параллельный счет осуществляется для точек, принадлежащий отрезку прямой длиной = 4.

DO 2 I=1, 4

DO 2 CONC FOR ALL J  { 4*(I-1) ≤ J ≤ MIN {4*I,15} }

X(I)=X(G*I-27)

2 CONTINUE

Общая постановка задачи.

Пусть I={I₁,I₂,…,I_n} – исходное пространство итераций. Требуется найти такие целые числа, P₁,P₂,…,P_n, называемые ребрами параллелепипеда, при которых исходные конструкции вида

DO 1 I₁=1,R₁

DO 1 I₂=1,R₂

……

DO 1 I_n=1,R_n

<ТЕЛО ЦИКЛА>

1 CONTINUE

ставится в соответствие эквивалентная конструкция вида

DO 2 CONC FOR ALL J  {1,N}

DO 2 K_j=1, P_j

DO 2 I₁=K₁, R₁, P₁

DO 2 I₂=K₂, R₂, P₂

……

DO 2 I_n=K_n, R_n, P_n

<ТЕЛО ЦИКЛА>

2 CONTINUE

Искомая конструкция создает для каждого набора K_i…K_n параллельную ветвь, представляющую собой вложенный цикл с шагами исполнения P₁ ….P_n. (1≤ K_j≤ P_j)

Для эквивалентности исходного и полученного цикла достаточно, чтобы в каждом из P₁*P₂…*P_n параллелепипедов не содержалось конкуренционно зависимых итераций, а так же порядок выполнения итераций группами, состоящими из параллелепипедов, был таков, чтобы все использования выполнялись после соответствующих генераций.

Поитерационая синхронизация метода: в каждой ветви осуществляется ожидание выполнения всех итераций одного и того же параллелепипеда.

Если не требовать выполнения условия прямоугольности параллелепипедов, то этот метод является естественным методом гиперплоскостей (гиперплоскость получается как параллелепипед, одна из сторон которого имеет длину =1 , а все остальные совпадают с границей R_k).

Данный метод может использоваться для простых циклов.

Для мин. времени выполнения результирующего цикла требуется, чтобы V пар-да был максимальный. Т.е. задача сводится к задаче целочисленного линейного программирования (решается в случае с линейными индексными выражениями).