99 Continue

Вычисляет среднее арифметическое между четырьмя точками.

Уравнение плоскости: 2*I+J+K = const

Для перехода к параллельному циклу используем переменные:

1 конструкция (прямое)	2 конструкция (обратное)	Результирующий (параллельный) цикл
I1, J1, K1: I1=2*I+J+K J1=I K1=K	I, J, K I = J1 J=I1-2*J1-K1 K=K1	DO 99 I=6,2*L+N+M DO 99 CONC FOR ALL (J1, K1)  { ( J1, K1): 1 ≤ J1 ≤ K1, 2 ≤ I1-2*J1-K1 ≤ M, 2 ≤ K1 ≤ N } (тело цикла для всех точек будет выполняться параллельно и независимо, причем для каждой точки может быть свой процессор; если количество процессоров соответствует количеству точек – получаем максимальное ускорение) V ( I1-2*J1-K1, K1 ) = ( V ( I1-2*J1-K1+1,K1 ) + V (I1-2*J1-K1, K1+1 ) + V (I1-2*J1-K1, K1 ) + V (I1-2*J1-K1, K1-1 ) ) *0.25 99 CONTINUE

В 1 конструкции количество повторений равно L*(M-1)*(N-1)

Во 2 новой конструкции 2*L+M+N-5 раз. Исходное пространство итераций сворачивается с 1-го по 3-х мерное. Выигрыш при больших M-N.

Общая постановка задачи:

DO A I¹=l¹, U¹

…

DO A Iⁿ=lⁿ, Uⁿ

<тело цикла>

A CONTINUE

Для использования метода гиперплоскостей необходимо, чтобы тело цикла не содержало:

• операторов ввода–вывода

• передач управления вне цикла

• обращений к процедурам и функциям, которые изменяют переменные в теле цикла.

Индексные выражения в операторах тела цикла должны иметь вид lⁱ+mⁱ, где lⁱ – i-я переменная, mⁱ - i-я константа. Разрешено I+2; запрещено I+J, I*2, I*J.

В результате применения метода гиперплоскостей исходный цикл преобразуется к виду:

DO A J¹=L¹, M¹

…

DO A J^k=L^k,M^k

DO A CONC FOR ALL (J^k+1, … Jⁿ)  S_Y¹_...Yⁿ

< тело цикла>

A CONTINUE

Максимальный выигрыш можно получить, когда все итерации в исходном цикле выполняются полностью, т.е. нет принудительного прекращения выполнения тела цикла.

Происходит свертывание пространственных операций, то есть изменение размерности на N-K

Для нахождения уравнения гиперплоскости строится взаимно-однозначное отображение переменных в теле исходного цикла в новые переменные. Это отображение ищется в виде:

Для нахождения коэффициентов а_jⁿ решается задача линейного целочисленного программирования, в которой формулируется ряд ограничений на коэффициенты а: в исходном и результирующем цикле все использования переменных должны следовать за их генерациями в теле цикла.

a=b. (a – использование, b – генерация.)

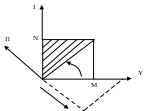
I₁ = a_{11 *} I + a_{12 *} J

J₂ = a_{21 *} I + a_{22 *} J

[-1 ÷ +1]

+1 – поворот на 45 градусов против часовой

-1 – по часовой.

Должен получиться один цикл перебора, но с вызовом #CALL () для каждой текущей линии.

«+»: метод хорошо формализован и, следовательно, он может быть использован в трансляторах с параллельных языков программирования для автоматического распараллеливания циклов; для каждой точки вычисления могут выполняться на отдельном процессоре и не требуется никакой синхронизации; мах. выигрыш если пространство итераций достаточно большое.

«-»: сложность получения алгоритма гиперплоскости а также неприменимость для некоторых видов циклов (в частности для простых циклов); неравномерность загрузки процессора;