Методичні вказівки і поради щодо розв’язування задач

Закон Ома визначає силу струму за спадом напруги або спад напруги за силою струму для найпростішого нерозгалуженого кола струму. Для складення системи рівнянь закон Ома в більшості випадків записують для замкнутого кола і для ділянки кола, на кінцях якої відома різниця потенціалів або ї потрібно знайти. Для обчислення струмів у більш складних розгалужених колах зручно користуватися двома законами Кірхгофа. Перед складанням рівнянь за законами Кірхгофа треба:

1) вибрати довільно напрями струмів у кожній вітці розгалуженого кола і вказати їх стрілками і

2) вибрати також довільно напрям обходу контуру При цьому слід завжди мати на увазі, що довільно обраний напрям обходу в даній задачі повинен бути однаковим для всіх контурів розгалуженого кола.

За першим правилом Кірхгофа слід складати на одно рівняння менше, ніж число вузлів, що є в колі, тому що рівняння для останнього вузла не буде незалежним, а тільки наслідком останніх рівнянь: його можна знайти їх додаванням.

При складанні рівнянь за першим законом Кірхгофа слід додержуватись правила знаків: струм, що надходить до вузла, в рівнянні позначається знаком «+». а струм, що йде від вузла, – знаком «–».

Число незалежних рівнянь, які можна скласти за другим законом Кірхгофа, також менше від числа замкнутих контурів. Щоб скласти потрібну кількість незалежних рівнянь, обов'язково треба додержуватися такого правила: для рівнянь вибирати контури так, щоб до кожного нового контуру входила хоча б одна вітка, що не використовувалась у жодному з попередніх контурів.

Складаючи рівняння за другим законом Кірхгофа, слід додержуватися такого правила знаків:

а) якщо напрям струму збігається з вибраним напрямом обходу контурів, то відповідний добуток сили струму на опір входить у рівняння із знаком «+», у противному разі цей добуток входить у рівняння із знаком «–»;

б) е.р.с. беруть із знаком «+», якщо при обході контуру в додатному напрямі перший електрод буде негативний, а другий – позитивний, тобто сторонні силі усередині джерела струму виконують позитивну роботу по переносу позитивного електричного заряду.

Загальне число рівнянь для вузлів і контурів має відповідати числу невідомих у задачі. Далі слід розв'язати систему рівнянь відносно шуканих величин.

В результаті розв'язування складених рівнянь шукані величини можуть вийти від'ємними. Якщо визначають сили струмів, то від'ємне значення вказує тільки на те, що справжній напрям струму на цій ділянці кола протилежний вибраному.

Приклади розв’язування задач

Задача 1. Напруга на клемах електричного кола, яке має опір R = 3 Ом, за час t = 20 c рівномірно зростає від U₀ = 2В до U = 4В. Визначити:

1. заряд, який пройшов по колу за цей час;

2. кількість тепла, яке виділиться у колі.

Розв’язання. Сила струму на ділянці кола у будь який момент часу визначається за формулою: І = dq/dt, відкіля заряд, який пройшов за час dt: . За законом Ома для однорідного провідника . Внаслідок рівномірного зростання напруги можливо записати: , де k – коефіцієнт пропорційності. Підставивши все це у формулу заряду, отримуємо:

. (1)

Проінтегрував рівняння (1), отримуємо:

. (2)

Коефіцієнт k знайдемо із умови, що у момент t₀ = 0 U₀ = 2В, а через t=t=20 c U = 4В:

. (3)

Підставивши (3) у (2), отримаємо кінцеву формулу для визначення електричного заряду:

.

Кількість тепла знайдемо за законом Джоуля–Ленца:

.

Враховуючи закон Ома і рівняння залежності напруги від часу, отримуємо:

. (4)

Проінтегрував рівняння (4) матимемо:

. (5)

Після підстановки (3) у (5), остання формула приймає вигляд:

= 62,2 Дж.

З адача 2. Потенціометр, опір якого R = 100 Ом підключили до акумулятора з внутрішнім опором r = 50 Ом, е.р.с.  якого дорівнює 150 В. Знайти рівняння залежності показань вольтметра з опором 500 Ом, який підключено так, як показано на малюнку, від довжини ділянки AB потенціометра. Що покаже вольтметр, якщо рухомий контакт потенціометра знаходиться посередині. Знайти різницю потенціалів на ділянці AB, якщо вольтметр від’єднати.

Р озв’язування. Рухомий контакт потенціометра сприяє розгалуженню струмів, тому опір R представимо як суму двох резисторів R₁ і R₂. Еквівалентна схема в цьому випадку показана на малюнку. Запишемо закон Ома для замкненого кола і для ділянки кола AB:

, .

Звідси знайдемо напругу, яку показує вольтметр:

(1)

Оскільки , то зробивши відповідну заміну в (1) і після деяких перетворень, отримуємо:

(2)

Із формули (2) випливає, що напруга вольтметра змінюється від 0 при правому положенні повзунка потенціометра А (R₂ = 0) до

при лівому положенні рухомого контакту А (R₂ = R).

Якщо рухомий контакт знаходиться посередині, то R₁ = R₂ = R/2 і напруга вольтметра буде дорівнювати

.

Якщо вольтметр від’єднати, то закон Ома для замкнутого кола і для ділянки з опором R/2 матиме вигляд:

і ,

звідси знаходимо:

Задача 3. Визначити опір залізного стержня (₀ = 0,12 Ом*м), температура одного кінця якого 0С, другого 800С. Довжина стержня L = 5 м, площа поперечного перерізу S = 1 см². Температурний коефіцієнт опору для заліза дорівнює  = 6*10^–3 К^–1. З бокової поверхні тепло не відводиться, залежністю коефіцієнта теплопровідності від температури нехтуємо.

Розв’язування. Тепло в стержні передається теплопровідністю. Оскільки з бокової поверхні стержня тепло не відводиться, а передається тільки вздовж стержня, то за законом Фур’є:

.

де – градієнт температури.

Через те, що температура кінців стержня підтримується незмінною, то процес теплопровідності є стаціонарним, причому права частина останнього рівняння залишається сталою. Отже

. (1)

Інтегруючи (1), визначимо закон зміни температури вздовж стержня:

,

звідки

, (2)

де – відстань до розглядуваного перерізу від кінця стержня, який має температуру t₁.

Питомий опір  при температурі дорівнює:

, (3)

де і – сталі величини. Опір стержня знайдемо за формулою:

. (4)

Підставивши в (4) a і b, отримуємо:

Ом.

Задача 4. Вольтметр, підключений до затисків джерела струму, показав 6 В. Коли до тих же затисків підключили резистор, вольтметр став показувати 3 В. Що покаже вольтметр, якщо замість одного підключити два таких же резистори, з'єднаних послідовно? паралельно?

Р озв’язування. Схема підключення вольтметра в електричне коло показана на рисунку. Знайдемо напругу на джерелі струму. Будемо вважати вольтметр ідеальним, тобто його опір дорівнює безкінченністі. Запишемо закон Ома для замкненого кола і для ділянки з опором R:

, ,

звідси отримаємо:

.

Отримана формула дозволяє знайти напругу, яку показує вольтметр у кожному випадку його підключення. Якщо зовнішній опір R відсутній, тобто , то , При наявності зовнішнього опору формули напруги вольтметра у кожному випадку мають вигляд:

, , .

Перепишемо отримані рівняння у вигляді:

, , .

Визначивши з першого рівняння і підставивши у друге і третє і враховуючи, що , отримаємо:

, .

З адача 5. Визначити силу струму, що проходить через опори R₁=R₄=2 Oм, R₃ = R₂ = 4 Oм, увімкнені в коло, як показано на рисунку, якщо Е₁=10 В, Е₂=4 В. Опорами джерел струму можна знехтувати.

Розв'язання. Тут маємо розгалужене коло; отже, щоб визначити сили струмів, застосовуємо закони Кірхгофа. Для розв'язання задачі треба скласти чотири рівняння (за кількістю невідомих величин – струмів). Виберемо довільно напрями струмів у кожній ділянці кола. Напрям обходу контурів виберемо за годинниковою стрілкою. За першим законом Кірхгофа для вузла В маємо:

. (1)

Запишемо другий закон Кірхгофа для контуру AR₁BR₂A:

, (2)

для контуру AR₁BR₃A:

(3)

для контуру AR₃BR₄A:

(4)

Розв'язуючи систему рівнянь (1) – (4) відносно струмів, знайдемо:

I1 = 3A, I2 = 0, I3 = –1A, I4 = 2A.

Знак «–» у числовому значенні струму I₃ свідчить про те, що він має протилежний напрям, тобто йде від вузла В до вузла А.

З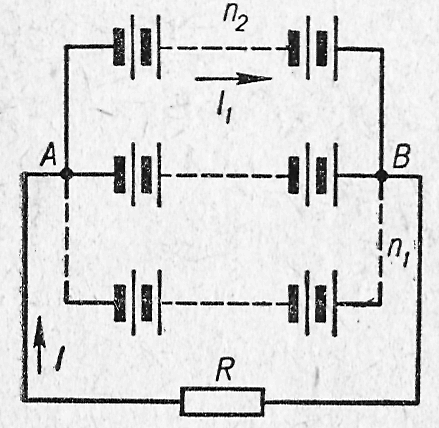 адача 6. Батарея із N = 400 елементів (е.р.с. кожного Е = 2 в і внутрішній опір г = 0,1 Ом) ввімкнена в коло з зовнішнім опором R = 10 Oм. Треба скласти змішану батарею із такого числа n₁ паралельних груп, кожна з яких включала б n₂ послідовно сполучених елементів, щоб дістати максимальну силу струму. Визначити числа n₁ і n₂, силу струму в опорі R і в кожному елементі.

Розв'язання. Застосуємо закони Кірхгофа. Як видно з рисунку, електричне коло має два вузли. Тому за першим законом Кірхгофа матимемо одне незалежне рівняння для вузла А:

(1)

За другим законом Кірхгофа для замкнутого контуру, в який входить опір R і одна з ділянок між точками А і В, матимемо рівняння:

(2)

Крім цього,

(3)

Підставивши в (2) значення І₁ з (1) і врахувавши (3), матимемо співвідношення для сили струму в колі:

(4)

Максимальна сила струму буде тоді, коли зовнішній опір дорівнюватиме внутрішньому опору батареї, тобто коли

, (5)

звідки знаходимо n₂:

.

Підставивши значення n₂ у (3), матимемо:

.

Отже, з урахуванням n₁ і n₂ максимальна сила струму дорівнює:

.

Сила струму в окремих елементах, згідно з (1), буде:

.

З адача 7. Знайти опір R між точками А і В для кола, зображеного на рисунку. Опори окремих віток показано на схемі.

Розв'язання. Увімкнемо цей опір у коло з е.р.с. Е і застосуємо закони Кірхгофа. Напрями струмів в окремих вітках показано на рисунку стрілками. На основі першого закону Кірхгофа для вузла А маємо:

(1)

для вузла С:

(2)

для вузла D:

(3)

Згідно з другим законом Кірхгофа, для контуру АСDА маємо:

(4)

для контуру СВDС:

(5)

для контуру АDВЕА:

(6)

Складаючи останнє рівняння, нехтуємо внутрішнім опором батареї.

Розв'язавши систему із шести рівнянь (1) – (6), знайдемо вираз для величини сили струму в колі:

.

Порівнюючи останню формулу з законом Ома , остаточно знайдемо опір R між точками А і В: .