- •Передмова
- •Глава 1.
- •1.1. Значення статистики як науки та практичної діяльності
- •1.2. Історія розвитку статистики
- •1.3. Основні теоретичні положення.
- •1.4. Питання для підготовки до занять, самоаналізу
- •Для нотаток
- •Глава 2.
- •2.1. Зміст і значення статистичного спостереження
- •2.2. Основні теоретичні положення.
- •2.3. Питання для підготовки до занять, самоаналізу
- •Для нотаток
- •Глава 3.
- •3.1. Зміст і значення статистичного узагальнення
- •3.2. Основні теоретичні положення.
- •Розділ 2. Грошові доходи сім’ї
- •Розділ 3. Грошові витрати сім’ї
- •3.3. Статистичні ряди. Задачі
- •3.4. Питання для підготовки до занять, самоаналізу
- •Для нотаток
- •Глава 4.
- •4.1. Зміст і значення статистичного аналізу
- •4.2. Основні теоретичні положення.
- •4.3. Статистичні таблиці та графіки
- •Для нотаток
- •4.4. Питання для підготовки до занять, самоаналізу
- •Для нотаток
- •Глава 5.
- •5.1. Зміст і значення статистичних показників
- •5.2. Основні теоретичні положення.
- •5.3. Задачі
- •5.4. Питання для підготовки до занять, самоаналізу
- •Для нотаток
- •Значення функції
- •Додаток 4 Інтеграл ймовірностей
- •Додаток 7 Критичні значення f-критерію
- •Додаток 8 Критичні значення Kn;α для статистики критерію Колмлогорова
- •Термінологія
- •Література
- •Умовні скорочення і символи
- •Покажчик змісту таблиць
- •Грецький алфавит
- •Латинський алфавит
Для нотаток
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
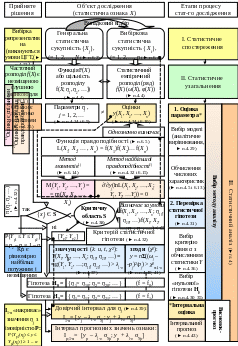
Рис. 4.1. Методологія статистичного аналізу
Ф Етапи дослідження |
Таблична |
Графічна |
Аналітична |
||||||
І. Статистичне спостереження (► гл.2) |
Статистичні таблиці (► п.4.44 і рис.4.3): |
Статистичні формуляри (► п.2.53) |
х |
х |
|||||
ІІ. Статистичне узагальнення (► гл.3) |
Статистичні звіти ( ► п.п.2.40 і 3.19) |
Діаграми, картограми, картодіаграми (► п.4.45 і рис.4.4) |
х |
||||||
Емпіричні функції розподілу (варіаційні ряди): многокутник розподілу (► п.3.28), гістограма (► п.4.40), кумулята (► п.4.41) |
+ |
||||||||
ІІІ. Статистичний аналіз (► гл.4) |
Розрахункові таблиці-матриці |
Система статистичних показників (► гл.5), в т.ч. числові характеристики закономірності (► § 4.2) |
|||||||
Вибірковий метод (► гл.6) |
Довірчий
і (► п.6.22) |
+ вибіркові розподіли
Теоре-тично |
В |
параметрів ГСС (► п.6.9) |
+ функціонали (квантилі, ► п.4.8) |
||||
Метод рядів динаміки (► гл.7) |
Діаграма ряду динаміки; модель сезонної хвилі |
+ лінія тренду
|
параметрів моделі тренду |
Показники динаміки (► § 7.2) |
|||||
КРАЗ (► гл.9) |
Кореляційне поле |
+ лінія регресії |
параметрів моделі регресії |
Показники зв’язку (►§§9.2, 3) |
|||||
Індексний метод (► гл.8) |
х |
Статистичні індекси (► § 8.2) |
|||||||
Рис. 4.2. Форми подання статистичної інформації (► п.3.19)
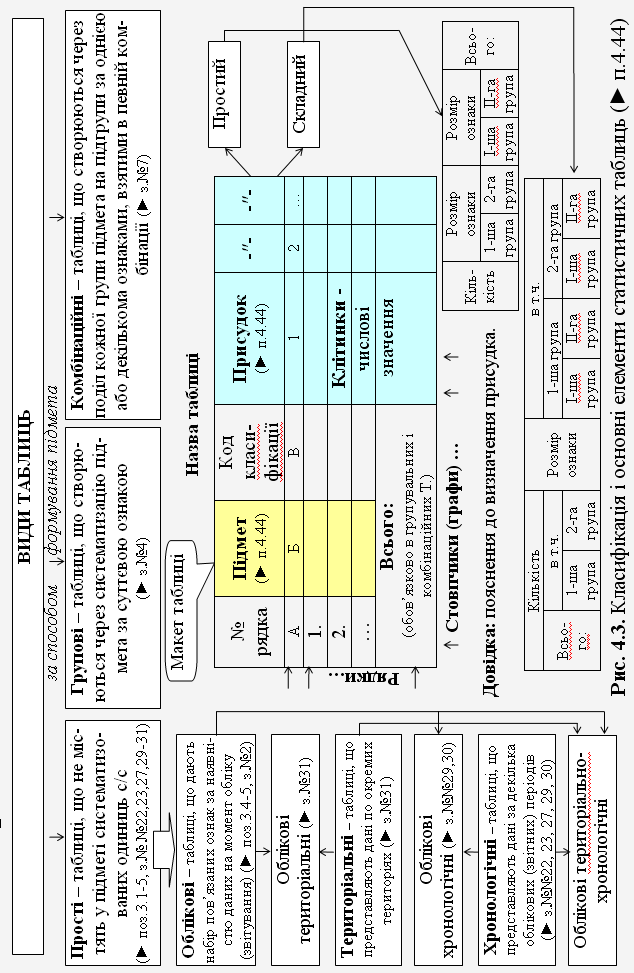
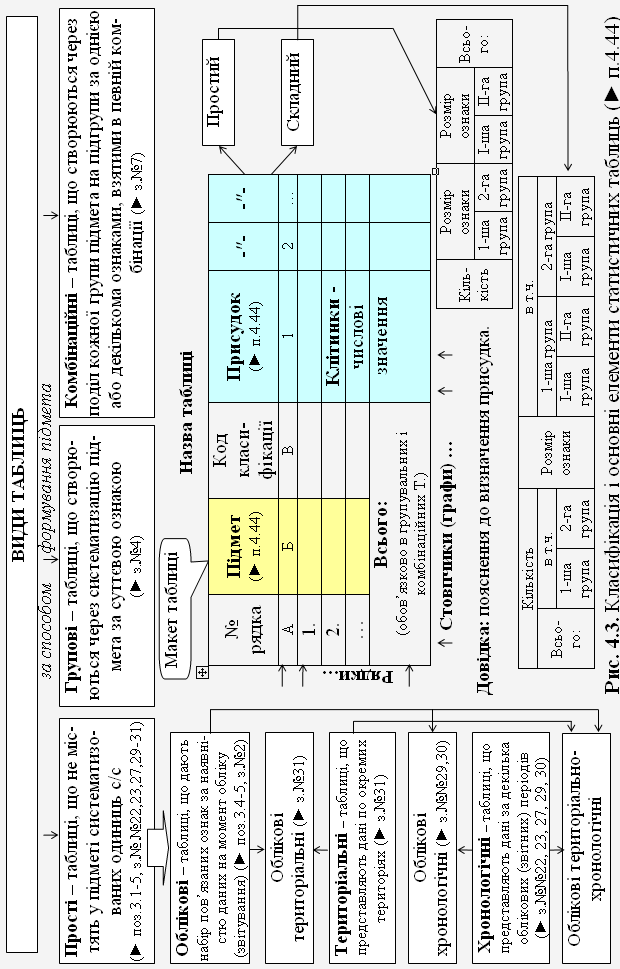
Таблиця 4
Термін (поняття) |
Визначення (формула) |
1 |
2 |
§ 4.1. Зміст статистичного аналізу (► рис.4.1) |
|
1. Статистичний аналіз (СА) |
Третій етап процесу статистичного дослідження соціально-економічних явищ (процесів), метою якого є виявлення властивих їм закономірностей (► п.4.5) на основі системи узагальнюючих статистичних показників (► п.4.2) відповідно до методів статистичного аналізу (► п.4.3). Основа СА – метод узагальнюючих статистичних показників (► п.1.9). Обраний метод статистичного аналізу (► п.1.9) та відповідні статистичні показники (► п.1.3) мають бути адекватними задачі дослідження (► п.1.11). |
2. Система узагальнюючих статистичних показників |
Основа статистичного аналізу (► рис.1.2); сукупність статистичних показників, обчислюваних по всіх одиницях досліджуваної сукупності або її окремої частини, таких, що представляють у цієї сукупності шукані закономірності у виді числових характеристик (чисел). Їх основу складають середні величини (► §5.3) і показники варіації (► §5.4), за допомогою яких обчислюються числові характеристики закономірностей статистичних розподілів (положення (► п.4.9), розсіювання (► п.4.10), асиметрії й ексцесу (► п.4.11) й ін.), показники динаміки (► §7.2), індекси (► §8.2), показники зв’язку (► §§9.2, 3). |
3. Метод (задачі) СА |
Комплекс методів, способів, прийомів, операцій, правил, необхідних для досягнення мети аналізу, розв’язання конкретної задачі або певної задачі з конкретного класу задач. Основним класам задач статистичного аналізу відповідають певні методи статистики (► п.1.9): 1) вивчення структури об’єкта дослідження відбувається за допомогою методів статистичних групувань, узагальнюючих статистичних показників; 2) оцінка просторових, часових змін ознаки, а також впливу факторів, що їх зумовлюють, здійснюється за допомогою методу рядів динаміки (► гл.7) й індексного методу (► гл.8); 3) виявлення й оцінка причинно-наслідкових (факторних) зв’язків між ознаками проводяться за допомогою КРАЗ (► гл.9). В основу цих методів покладений принцип несуцільного вибіркового статистичного дослідження (► гл.6).
|
Продовження таблиці 4
1 |
2 |
3. Метод (задачі) СА (продовження) |
Дві головні задачі методу – оцінка параметра (► п.4.24) і перевірка статистичної гіпотези (► п.4.31). До поширених конкретних задач статистичного аналізу відносять: аналітичне вирівнювання у статистичних рядах (► п.4.29); пошук основної тенденції розвитку (тренду, регресії) (► §§7.3, 9.2), прогнозування (►§§7.4, 9.6) та вивчення сезонних коливань в рядах динаміки (► §7.5); індексація статистичних сукупностей (► §8.1). У комплексі, крім того, застосовуються такі поширені методи: максимальної правдоподібності (► п.6.15) та найменших квадратів (► п.п.7.16, 9.12), апроксимації (► п.7.16) й екстраполяції (► п.7.23) (у вибіркових дослідженнях, рядах динаміки, КРАЗ), збільшення інтервалів (► п.7.28) і плинного середнього (► п.7.29) (в рядах динаміки щодо виявлення тренду) й ін. До поширених способів відносять наступні: відліку часу від умовного початку (► п.7.16) (у рядах динаміки щодо визначення параметрів моделі тренду), постійного (змінного) середнього (► п.7.31) (в рядах динаміки щодо побудови моделі сезонної хвилі), визначників (щодо визначення параметрів моделей тренду в рядах динаміки (► п.7.16) й регресійних моделей в КРАЗ (► п.9.12)) й ін. |
§ 4.2. Статистичний закон і закономірність |
|
4. Закон розподілу ймовірностей випадкової величини |
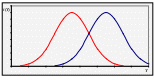
Співвідношення, що встановлює залежність між імовірністю випадкової величини X і значеннями цієї випадкової величини х, найчастіше: у значеннях її ймовірностей21 p(x) = P{X = x}, функції F(x) = P{X < x}22 або щільності f(x) = dF/dx23 розподілу її ймовірностей (остання характеристика справедлива для неперервних величин). Закони розподілу випадкових величин застосовують як імовірнісні моделі у статистичному аналізі досліджуваних ознак (статистик), характеризуючи залежність між числовою характеристикою чисельності статистичної ознаки X (статистики) і значеннями цієї ознаки х (статистики) у статистичних рядах (розподілах) (► п.3.20). |
Продовження таблиці 4
1 |
2 |
5. Закономірність розподілу |
Властивість розподілу, що має прояв у його узагальнюючих числових характеристиках (моментах): квантилях (статистиках, ► п.4.8), характеристиках положення (середніх величинах, ► п.4.9), характеристиках розсіювання (показниках варіації, ► п.4.10), характеристиках асиметрії й ексцесу (► п.4.11). |
6. Початковий момент порядку r (Mr(Х) або Mr) |
Числова характеристики закономірності розподілу ймовірностей дискретної та неперервної випадкових величин (положення), яка дорівнює відповідно:
У статистичних рядах p(X) набуває змісту частості ω. |
7. Центральний
момент порядку r
( |
Числова характеристики закономірності розподілу ймовірностей дискретної та неперервної випадкових величин (розсіювання), яка дорівнює відповідно:
У статистичних рядах p(X) набуває змісту частості ω. |
8. Квантиль (xq) порядку q (
|
Таке значення xq випадкової величини (ознаки) Х, для якого існує ймовірність q = Р{X < xq} = F(xq) (0 < q < 1). У розподілах розрізняють такі квантилі: х1/2 – медіану; х1/4 , х2/4 , х3/4 – квартилі; х1/10, х2/10, …, х1/10, х2/10, х9/10 – децилі; х1/100, х2/100, …, х99/100 – процентилі. процентилі. Рис. Квантиль xq розподілу f(x). |
9. Характеристики положення (середні величини) |
1) Центр розподілу (математичне сподівання)
M(X) = mХ.
2) Медіана Me = х1/2.
3) Мода (Mo): найчисельніше (найімовірніше) значення Х (розподіл з однією, двома і більше модами називають відповідно одно-, двох- і багатомодальним). |
Продовження таблиці 4
1 |
2 |
10. Характеристики розсіювання (показники варіації)
|
1) Розмах варіації (R) – різниця між найбільшим xmax і найменшим xmin значеннями випадкової величини (ознаки) Х: R = xmax – xmin.
2) Середнє
лінійне абсолютне відхилення
( = M(|X – mХ|). 3) Дисперсія (D(Х), або D, або σХ2):
D = M((X – mХ)2).
4) Середнє квадратичне відхилення (СКВ, σХ):
σХ = √ D. 5) Інтерквартальна широта х3/4 – х1/4 і (10-90)-процентильна широта х90/100 – х10/100. 6) Півширота одномодального неперервного розподілу – піврізниця двох значень Х, у котрих f(X) = maxf(X)/2 = f(mХ)/2. |
11. Характеристики асиметрії й ексцесу |
1) Коефіцієнт асиметрії: 2) Коефіцієнт ексцесу:
3) Пірсонівська міра асиметрії одномодального розподілу:
|
Типові теоретичні розподіли |
|
12. Біноміальний розподіл b(k; N, p) (Бернуллі)
|
Розподіл (з параметрами N і p) ймовірностей дискретної випадкової величини Х, яка набуває невід’ємного цілого значення k з ймовірністю (інакше, ймовірність того, що випадкова подія трапляється k раз у N можливих випробуваннях):
де
кількість k-елементних сполучень; p – імовірність події в кожному випробуванні (0 < p < 1).
Рис. Біноміальний розподіл b(k;N,p) з N = 8 і p = 0,2. |
Продовження таблиці 4
1 |
2 |
13. Умови, за яких розподіл Бернуллі зводиться до розподілу Пуассона |
Якщо N → ∞, p → 0, а Np має скінченну границю λ > 0, то біноміальний розподіл зводиться до розподілу Пуассона (► п.4.14) (апроксимується останнім) з центром Np і дисперсією Np (закон «малих» чисел). |
14. Розподіл П p(k; λ) |
Розподіл (з фіксованим параметром λ = Np > 0) ймовірностей дискретної випадкової величини Х, яка набуває невід’ємного цілого значення k з ймовірніс- тю:
де p – імовірність події в кожному випробуванні (0 < p < 0,1).
Рис. Розподіл Пуассона з λ =0,5 |
15. Умови, за яких біноміальний розподіл зводиться до нормального |
Якщо N → ∞, 0 < (p = const) < 1, а Np → ∞, то біноміальний розподіл є асимптотично нормальним з центром Np і дисперсією Np(1 – p) (теорема Муавра-Лапласа, поодинокий випадок центральної граничної теореми). |
16. Нормальний розподіл (Гауса, або N-розподіл) (f(x)) |
Розподіл ймовірностей неперервної випадкової величини Х з математичним сподіванням mХ і дисперсією σХ2, який має щільність (крива розподілу – гаусіана):
|
17. Стандартизована нормальна величина (и-розподіл) |
Неперервна випадкова величина U = (X – mХ) / σХ, яка має розподіл Гауса (представлена щільністю f(u) або функцією розподілу F(u)) з нульовим математичним сподіванням і одиничною дисперсією (гаусіаною):
інтеграл Лебега-Стілтьєса. В області визначення U від 0 до +∞ значення f(U) і F(U) представлені статистичними таблицями (► Д.3, 4). |
Продовження таблиці 4
1 |
2 |
17. и-розподіл (продовження)
Рис. 1. Щільність стандартизованого нормального розподілу f(U).
Рис. 2. Інтегральна функція стандартизованого нормального розподілу F(U). |
ФU(X)
и
ФU(X)
и
|
18. Інтеграл ймовірностей Лапласа (ФU(u)) (► Д.4) |
Імовірність того, що неперервна випадкова величина U набуває значень в інтервалі від 0 до u (► п.4.17/рис.):
|
19. Деякі властивості нормального розподілу |
1) f(±∞) → 0, fmax(x) = f(mХ) = 1/√(2π), f(x)= fU(u)/σХ; 2) mХ = Mo = Me, γ1= γ2 = 0;
функція похибок erfz ≡ -erf(-z) = 2FU(z√2) – 1;
|
Продовження таблиці 4
1 |
2 |
19. Деякі властивості нормального розподілу (продовження) |
Типові значення k і відповідні значення p: k = {1; 2; 3} і p = = {0,683; 0,954; 0,997}. 5) Квантилі, що обираються в якості довірчих границь U (α-значень U) (► п.п.4.17, 38, 39):
Типові α-значення U (α = {0,05; 0,01; 0,001}):
|u|0,95 = u0,975 ≈ 1,96, |u|0,99 = u0,995 ≈ 2,58, |u|0,999 = u0,9995 ≈ 3,29.
6) Характеристики розсіювання: - середнє абсолютне відхилення
M|X – mX| = σM|u| = √(2/π)σ ≈ 0,798σ.
- імовірне відхилення, або Me(|Х – mХ|): |u|1/2σХ = -u1/4σХ = u3/4σХ ≈ 0,674σХ. - половина півшироти: √(2ln2)σ ≈ 1,177σ. - нижній і верхній квартилі: x1/4 = mX + u1/4σ = mX – |u|1/2σ, x3/4 = mX + u3/4 = mX + |u|1/2σ. - міра точності: h = 1/(σ√2). |
20. t-розподіл (Стьюдента)
|
Неперервна випадкова величина Х має t-розподіл з m ступенями свободи (m – натуральне число) в області визначення від -∞ до +∞, якщо щільність її ймовірності можна представити формулою
3
2
1 Г(1) = 1, Г(1/2) = √π.
Рис. Щільність t-розподілу для різних значень ступенів свободи m: 1) m = 1, 2) m = 2, 3) m = ∞ |
Продовження таблиці 4
1 |
2 |
20. t-розподіл (продовження) |
Властивості розподілу: 1) f(±∞) → 0, f(-х) = f(+х), maxf(X) = f(0). 2) Числові характеристики: а) математичне сподівання М(Х) = 0 (m > 1); б) дисперсія D(X) = m/(m – 2) (m > 2); в) мода і медіана Мо = Ме = 0; г) коефіцієнт асиметрії γ1=0 (m > 3); ґ) коефіцієнт ексцесу γ2 = 3(m – 2)/(m – 4) (m > 4); д) момент r-го порядку(r ≤ m – 1, m > 2)(відносно Х = 0).
3) Типова інтерпретація. Якщо m випадкових величин X0, X1, …, Xm взаємно незалежні та нормально розподілені з нульовим математичним сподіванням і дисперсіями σХ², то випадкова величина
має t-розподіл з m ступенями свободи. T від σХ² не залежить. 4) Квантилі tm;р = -tm;1-р за рахунок симетричності розподілу. До того ж, |t|m;1-α = tm;1-α/2, що відповідає рівності P{|T| > |t|m;1-α} = = α. Ці квантилі зведені у статистичні таблиці (► Д.6). 5) Наближення. Якщо m → ∞, тоді t-розподіл є асимптотично нормальним з центром 0 і дисперсією 1, так, що tm;р ≈ uр, |t|m;1-α = t m;1-α/2 ≈ |u|1-α = u1-α/2 для N > 30 (► п.п.4.33 і 6.8). |
21. χ²-розподіл (
1 |
Неперервна випадкова величина Х має χ²-розподіл з m ступенями свободи (m – натуральне число) в області визначення від -∞ до +∞, якщо щільність її ймовірності можна представити формулою
1
2
3
Рис. Щільність χ²-розподілу для різних значень ступенів свобо- ди m: 1)m = 1; 2) m = 2; 3) m = 6 |
Продовження таблиці 4
1 |
2 |
21. χ²-розподіл (продовження) |
Властивості розподілу: 1) f(+∞) → 0. 2) Числові характеристики: а) математичне сподівання М(Х) = m; б) дисперсія D(X) = 2m; в) мода Мо = m – 2 (m ≥ 2); г) коефіцієнт асиметрії γ1 = 2√(2/m); ґ) коефіцієнт ексцесу γ2 = 12/m; д) момент r-го порядку (відносно Х = 0)
3) Типова інтерпретація. Якщо m взаємно незалежних стандартизованих випадкових величин Uj = (Xj – M(Xj))/σXj мають нормальні розподіли, то сума їх квадратів
має χ²-розподіл з m ступенями свободи. 4) Квантилі χ²m;p або χ²m;1-α зведені у статистичні таблиці (► Д.5). 5) Наближення. Якщо m → ∞, тоді - Х розподілена асимптотично нормально з центром m і дисперсією 2m; - Х/m розподілена асимптотично нормально з центром 1 і дисперсією 2/m; - √(2X) розподілена асимптотично нормально з центром √(2m – 1) і дисперсією 1, так, що
χ²m;p ≈ 1/2(√(2m – 1) + Up)²
для m > 30 (► п.п.4.33 і 6.8). Up – квантилі стандартизованого нормального розподілу. Ця апроксимація непридатна при p наближених до 0 або до 1. Кращою щодо цього є апроксимація
|
Продовження таблиці 4
1 |
2 |
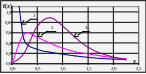
22. F-розподіл ( |
Неперервна випадкова величина Х має F-розподіл з k1 і k2 ступенями свободи (k1 і k2 – натуральні числа) в області визначення від -∞ до +∞, якщо щільність її ймовірностей можна представити формулою
де В – бета-функція25.
Рис. Щільність F-розподілу для різних значень с ступенів свободи k1 і k2: 1) k1 = 1 і k2 = 4; 2) k1 = 4 і k2 = 2; 3) k1 = 10 і k2 = 50
Властивості розподілу: 1) f(+∞) → 0. 2) Числові характеристики: а) математичне сподівання М(Х) = k2/(k2 – 2) (k2 > 2); б) дисперсія D(X) = 2k2²(k1 + k2 – 2)/(k1(k2 – 2)²(k2 – 4)) (k2 > 4); в) мода Мо= k2(k1 – 2)/ k1(k2 + 2) (k1 > 2); г) момент r-го порядку (відносно Х = 0)
3) Типова інтерпретація. Якщо k1 + k2 взаємно незалежних випадкових величин Хi (i = 1, 2, …, k1) і Xj (j = 1, 2, …, k2) мають нормальні розподіли з центрами 0 і дисперсіями σХ², то відношення двох випадкових величин |
Продовження таблиці 4
1 |
2 |
22. F-розподіл (продовження) |
що мають χ²-розподіли з k1 і k2 ступенями свободи відповідно, підпорядковано F-розподілу з k1 і k2 ступенями свободи. F від σХ² не залежить.
має бета-розподіл.
Змінна
4) Квантилі Fk1,k2;1-α = 1/Fk2,k1;α зведені у статистичні таблиці (► Д.7). 5) Наближення. Якщо k1 → ∞, k2 → ∞, тоді величина Z розподілена асимптотично нормально з центром (k1 – – k2)/(2k1k2) і дисперсією (k1 + k2)/(2k1k2). Ця апроксимація є придатною для k1 > 30 і k2 > 30 (► п.п.4.33 і 6.8). |
23. Центральна гранична теорема (ЦГТ) (умови нормалізації розподілів) |
Якщо випадкова величина являє собою суму N взаємно незалежних випадкових величин Хі (i = 1, …, N) із скінченними математичними сподіваннями mХi і дисперсіями σХi2, то при необмеженому збільшенні їх кількості (N → ∞) вона має асимптотично нормальний розподіл з центром ΣmХi і дисперсією ΣσХi2, до того ж, для будь-якого додатного числа ε існує границя (умови Ліндеберга):
Якщо
Хі
мають один і той же самий розподіл
ймовірностей із скінченим математичним
сподіванням mХ
і загальною дисперсією σХ2,
то випадкова величина
|
Продовження таблиці 4
1 |
2 |
§ 4.3. Методологія статистичного аналізу (► рис.4.1) |
|
24. Параметр і його оцінка
|
Таке уточнення параметра η розподілу статистичної ознаки Х в генеральній сукупності (► п.6.2), ідеалізованого певною імовірнісною моделлю F(Х) з тим же самим параметром, по даних (X1, X2, …, Xn) вибіркового дослідження (вибірки (► п.6.4)), що дає певну статистику (вибіркову оцінку (► п.6.10)) Y(X1, X2, …, Xn), яка надійно (► п.4.25) представляє цей параметр своїм значенням yj = y(x1, x2, …, xn) (j = 1, 2, …), отриманим по реалізації вибіркових даних (x1, x2, …, xn). Поширені оцінки – вибіркові частка та середнє арифметичне. Оцінка може бути точковою й інтервальною (► п.4.39). |
25. Властивості надійної оцінки |
Шукана оцінка є надійною, якщо вона є слушною (► п.4.26), незміщеною (► п.4.27) й ефективною (► п.4.28). Вона може бути достатньо надійною, якщо задовольняє хоча б однієї з цих властивостей. |
26. Слушна оцінка |
Така оцінка Y параметра η, яка при n → ∞ наближається по ймовірності до значення параметра η:
Різниця Δj = yj – η є похибкою оцінювання і має випадковий характер. |
27. Незміщена оцінка |
Така оцінка Y параметра η, математичне сподівання якої M(Y) дорівнює значенню параметра η:
Величина |M(Y) – η| є зміщенням оцінки. |
28. Ефективна оцінка |
Така оцінка Y параметра η (обов’язково незміщена та слушна), дисперсія якої існує й є найменшою для асимптотично нормальних (► п.6.11/2) розподілів f(Y) із середнім η і дисперсією D(Y) = λ/n:
Відношення
|
Продовження таблиці 4
1 |
2 |
29. Аналітичне вирівнювання26 статистичного розподілу |
Процедура розповсюдження властивостей певного теоретичного розподілу ймовірностей випадкової величини на числові характеристики статистичного розподілу частоти (частості, щільності) досліджуваної ознаки з метою їх наближеного взаємного представлення (з певною ймовірністю або на певному рівні значущості (► п.4.35)). Типові інтерпретації: 1) представлення статистичного (емпіричного) ряду теоретичною функцією (гаусіаною, розподілом Пуассона й ін.) з параметрами, що дорівнюють аналогічним емпіричним числовим характеристикам закономірності (► п.4.5); 2) представлення основної тенденції розвитку в ряду динаміки (► п.7.15) та 3) факторного зв’язку між ознаками (► п.9.4) адекватною математичною функцією (► п.п.7.17 і 9.13) (відповідно трендом (► п.7.15) і лінією регресії (► п.9.10)) з використанням методу найменших квадратів (► п.п.7.16 і 9.12). |
30. Статистична гіпотеза |
Припущення про певний можливий закон розподілу F(X) або f(X) статистичної ознаки Х у вибірковій сукупності, або про значущість вибіркової оцінки Y. Гіпотеза може бути простою і складною (► п.4.34). |
31. Перевірка статистичної гіпотези |
Для перевірки статистичних гіпотез, які встановлюють деякі властивості теоретичного розподілу (η), оцінюється правдоподібність досліджуваної вибірки за умови, що для обчислення функції правдоподібності (► п.6.5) застосовується передбачувана щільність розподілу f(X). Перевірка виконується за певними статистичними критеріями, або критеріями статистичних гіпотез (► п.4.32). |
32. Критерій статистичної гіпотези |
Нехай задана деяка фіксована вибірка об’єму n (► п.6.4); критерій статистичної гіпотези Н – це правило, що дозволяє спростувати або прийняти гіпотезу Н за умов вибірки {х1, х2, …, хn}. Кожен критерій визначає критичну множину (область) S «точок» (Х1, Х2, …, Хn): гіпотеза відкидається як хибна (спростовується), якщо вибірка {х1, х2, …, хn} належить критичній множині, або потрапляє в область малої правдоподібності, тобто вибіркова статистика Y(Х1, Х2, …, Хn) малоймовірна за обраною гіпотетичною функцією правдоподібності (► п.6.11/3), й вважається істинною у протилежному випадку. |
Продовження таблиці 4
1 |
2 |
3 |
Таке прийняття або відкидання гіпотези не дає логічного її доказування або спростовування. Тут можливі чотири ситуації: а) гіпотеза Н є вірною та приймається згідно критерію; б) гіпотеза Н є невірною (хибною) та відкидається згідно критерію; в) гіпотеза Н є вірною, але відкидається згідно критерію (похибка першого роду (► п.4.35)); г) гіпотеза Н є невірною (хибною), але прийма- ється згідно критерію (похибка другого роду). Для будь-якої множини фактичних значень параметрів η1, η2, … ймовірність відкинути гіпотезу по даній критичній області S дорівнює
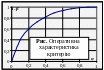
Якщо з гіпотезою Н конкурує лише одна альтернативна проста гіпотеза Н1 ≡ {η1 = η11, η2 = η21,…}, то ймовірність πS(η11, η21,…) відкинути гіпотезу Н, коли є вірною гіпотеза Н1, називають потужністю критерію, що визначений на S, по відношенню до гіпотези Н1. Залежність імовірності (1 – β) правильного відкидання гіпотези Н від імовірності α хибного її відкидання називають оперативною характеристикою критерію (рис.). |
33. Кількість ступенів свободи критерію |
Кількість «вільних» елементів даних, на які не накладені обмеження при обчисленні статистики вибірки або критерію перевірки. Інакше, це – кількість одиниць статистичної сукупності, які можуть набувати довільних значень, не змінюючи середнього значення ознаки. Наприклад, сукупність чотирьох (N = 4) вибіркових чисел 16, 21, 25, 30 дає середнє арифметичне число 23; їх відхилення від середнього становлять -7, -2, 2, 7 відповідно; сума відхилень дорівнює 0. Якщо необхідно зберегти значення середнього для інших чотирьох вибіркових чисел, лише три перших з них можуть набувати вільних значень, наприклад: 15, 22, 24, – четверте ж має бути таким, щоб забезпечити нульову суму чотирьох їх відхилень від середнього (-8 + (-1) + 1 + Δ4 = 0, Δ4 = 0 – (-8) – (-1) – 1 = 8, х4 = 23 + 8 = 31). Отже, значення четвертого елемента сукупності, х4 = 31, залежить від значень перших трьох її елементів, а тому кількість ступенів свободи m цього критерію (оцінки схожості чи відмінності величин середніх двох вибірок) з одним оцінюваним параметром, середнім арифметичним, (кількість параметрів s = 1) становить m = N – s = 4 – 1 = 3. |
Продовження таблиці 4
1 |
2 |
34. Проста та складна статистичні гіпотези |
Статистична гіпотеза, яка однозначно визначає розподіл ймовірностей n-мірної величини (Х1, Х2, …, Хn) з параметрами η1=η10, η2=η20, …, що є координатами «точки» в просторі параметрів, вважається простою. У протилежному випадку (неоднозначна визначеність розподілу) гіпотеза є складною і обмежує «точки» η1, η2, … деякою областю в просторі параметрів. |
35. Рівень значущості критерію (
Критична
область
(спростування
Н0)
Y1
– α/2
S
= α/2
Гіпотеза
Н0
|
Бажано вибрати таку критичну область, щоб імовірність πS(η1, η2, …) була малою, якщо гіпотеза, яка перевіряється, є вірною, й значною в протилежному випадку. Нехай критична область S застосовується для перевірки простої гіпотези Н0 ≡ {η1 = η10, η2 = η20, …} («нульова гіпотеза»), і нехай вона є вірною, тоді ймовірність даремно відкинути гіпотезу Н0 (похибка першого роду) є πS(η10, η20, …) = α; α називають рівнем значущості даного
Критична
область
(спростування
Н0)
Область
прийняття Н0
S
= α
рівні значущості α.
S
= 1 – β
S
= β
Гіпотеза
Н1
S
= α/2
Рис. Перевірка гіпотези Н0
при н
Y1
+ α/2
η
η
+ ∆
|
36. Правило Неймана-Пірсона відбору критеріїв для простих гіпотез |
1. Найбільш потужний критерій для простої гіпотези Н0 ≡ {η1 = η10, η2 = η20, …} відносно простої альтернативної гіпотези Н1 ≡ {η1 = η11, η2 = η21, …} визначається такою критичною областю S, яка дає найбільше значення ймовірності πS(η11, η21, …). 2. Рівномірно найбільш потужний критерій є найбільш потужним критерієм відносно всіх доступних альтернативних гіпотез; він не завжди існує. 3. Критерій є незміщеним, якщо πS(η11, η21, …) ≥ α для кожної простої альтернативної гіпотези Н1; в протилежному випадку критерій є зміщеним. Найбільш потужний незміщений критерій відносно даної альтернативної гіпотези Н1 і рівномірно найбільш потужний незміщений критерій відокремлюються з незміщених критеріїв.
|
Продовження таблиці 4
1 |
2 |
36. Правило Неймана-Пірсона (продовження) |
Критична область S для найбільш потужного критерію будується так, щоб для всіх вибіркових точок (Х1, Х2, …, Хn) відношення правдоподібності
f(Х1, Х2, …, Хn; η10, η20, …)/f(X1, X2, …; η11, η21, …) або р(Х1, Х2, …, Хn; η10, η20, …)/р(X1, X2, …; η11, η21, …)
було меншим за деяке постійне С; різні значення С даватиме «кращі» критичні області при різних рівнях значущості α. Рівномірно найбільш потужний критерій є доречним щодо перевірки гіпотези Н0 по відношенню до складної альтернативної гіпотези. Практично у виборі критерію переважаючою може стати легкість обчислень. Звичайно потужність критерію можна підвищити через збільшення об’єму вибірки n. |
37. Критерій значущості |
Нехай властивість ГСС, що перевіряється, зводиться до множини значень параметрів η1 = η10, η2 = η20, …, які порівнюються з вибірковими оцінками цих параметрів. В якості основи критерію намагаються побудувати таку статистику
Y = Y(Х1, Х2, …, Хn; η10, η20, …) ≡ ≡g(Y1, Y2, …; η10, η20, …),
значення якої вимірюють відхилення або відношення порівнюваних параметрів генеральної сукупності (► п.6.9) й їх вибіркових оцінок (► п.6.10). При цьому проста гіпотеза Н0 ≡ {η1 = η10, η2 = η20, …} відкидається із даним рівнем значущості α («відхилення» є значущим), якщо вибіркова оцінка Y потрапляє поза можливий інтервал {Yр1 ≤ Y ≤ Yр2} = р2 – р1 = = 1 – α. Відповідна оцінка параметра є незначущою. У протилежному випадку оцінка є значущою. Критерії, визначені в такий спосіб, називають критеріями значущості. Остання формула визначає Yр1= Yр1(η10, η20, …) і Yр2= Yр2(η10, η20, …) як квантилі вибіркового розподілу статистики Y(Х1, Х2, …, Хn; η10, η20, …). Часто вдається вибрати статистику Y так, що її квантилі Yр були б незалежними від η10, η20, … . Yр1 і Yр2 називають границями довірчого інтервалу [Yр1 ; Yр2] (► п.4.39) на заданому рівні значущості α. Поширені критерії: t (Стьюдента) (► п.4.20), χ² (Пірсона) (► п.4.21), F (Фішера) (► п.4.22). |
Продовження таблиці 4
1 |
2 |
38. Довірча область рівня α (Sα) |
Нехай побудовано
сімейство критичних областей Sα(η1,
η2,
…) для перевірки множини простих
гіпотез (допустимих комбінацій
параметрів η1,
η2,
…) при певному заданому рівні значущості
α27.
Тоді для будь-якої фіксованої вибірки
(Х1
= х1,
…, Хn
= xn)
множина Dα(x1,
x2,
…, xn)
комбінацій параметрів (η1,
η2,
…) (точок у просторі параметрів), які
узгоджуються з даною вибіркою, є
довірчою областю рівня α;
(1 – α)
називають довірчою
ймовірністю (ε).
Довірча область містить усі допустимі
комбінації параметрів, прийняття
яких на основі даної вибірки має
ймовірність Р{(x1,
x2,
…, xn) |
39. Довірчий інтервал (Іα) (геометрична інтерпретація) (► п.6.22) |
Y
Yр2
(η1)
Yр1(η2)
γ1 знайти довірчу область, що пов’язує значення одного з
γ2
y Y(x1, x2, …, xn) підхожої статистики Y (рис. 1). Yр1(η1) і Yр2 (η1) – нижня і верхня границі допуску в
η1
=
η11
η1
Рис. Визначення довірчих інтервалів
Перетин граничних кривих з кожною прямою Y = y визначає нижню і верхню границі γ1 = γ1(y), γ2 = γ2(y) довірчого інтервалу Іα ≡ [γ1; γ2] рівня α28. Довірчий інтервал містить такі значення параметра η1, прийняття яких на основі вибіркового значення Y = y має ймовірність (довірчу) Р{Yр1(η1) ≤ y ≤ Yр2(η1)} ≥ (1 – α) (► п.6.18). |
40. Критерій згоди |
Статистичний критерій, який контролює узгодженість гіпотетичних ймовірностей pj = P{Ej} випадкових подій E1, E2, …, Er з їх відносними частотами ωj = W{Ej} = fj/n у вибірці з n незалежних спостережень. У багатьох застосуваннях кожна подія Ej полягає в тому, що деяка випадкова величина Х потрапляє в певний j-й класовий |
Продовження таблиці 4
1 |
2 |
40. Критерій згоди (продовження) |
інтервал, так що цей критерій дозволяє порівнювати гіпотетичні (теоретичні) розподіли величини Х з її емпіричним розподілом за допомогою відповідної статистики. Поширеними є критерії згоди χ² (► п.4.41), А.М.Колмогорова (► п.4.42), Мізеса29. |
41. Критерій згоди χ² (Пірсона) |
Узгодженість за цим критерієм вимірюється за допомогою статистики
де pj – імовірність того, що випадкова величина Х набуває значень в j-му класовому інтервалі (j = 1, …, n); fj і npj – фактична і теоретична абсолютні частоти інтервальної ознаки. Розподіл статистики Y при n → ∞ наближається до розподілу χ² (► п.4.21) з m = r – 1 ступенями свободи. Правила застосування критерію. 1) Якщо всі npj > (5…10)30, то критерій χ² спростовує гіпотетичні ймовірності з рівнем значущості α при Y > χ²m;1-α. Якщо m > 30, то замість χ²-розподілу можна застосовувати нормальний розподіл величини √(2χ²) з центром √(2m – 1) і дисперсією 1. 2) Якщо гіпотетичні ймовірності pj залежать від s невідомих параметрів η1, η2, …, ηs, то спочатку знаходять спільні найбільш правдоподібні оцінки цих параметрів по даній вибірці й підставляють отримані значення pj = pj(η1, η2, …, ηs) у формулу статистики Y. За достатньо загальних умов31 статистика Y збігається по ймовірності з χ² з m = r – s – 1 ступенями свободи й критерій χ² є застосовуваним з m = r – s – 1. |
Продовження таблиці 4
1 |
2 |
42. Критерій згоди А.М.Колмо-горова |
Узгодженість за цим критерієм вимірюється за допомогою статистики
де Fn(Х) – емпірична ступінчаста функція розподілу32, побудована по даних вибірки (х1, х2, …, хn) об’єму n після її впорядкування зі збільшенням Х, так, що
F(Х) – теоретична неперервна функція розподілу генеральної сукупності, узгодженість з якою перевіряється. Розподіл статистики √n ∙ Dn при n → ∞ наближається до розподілу Колмогорова33:
Правила застосування критерію. 1) Рівень значущості α вибирається з умови Р{√n ∙ Dn > x} = = α = 1 – K(x), у припущенні що неможливо отримати цю рівність, коли існує відповідність між функціями F(X) i Fn(X). 2) Гіпотеза Н0 спростовується, якщо розрахункове значення статистики Dn перевищує критичне значення двостороннього34 критерію Колмогорова на рівні значущості α: dn = max(Dn+, Dn-) > Kn; α, – за умов, що
|
Продовження таблиці 4
1 |
2 |
43. Статистичний прогноз |
Оцінка значення однієї випадкової величини (ознаки) у виді функції значень інших випадкових величин (ознак). Поширеними є такі задачі прогнозування: 1) екстраполяція в рядах динаміки (► п.7.23); 2) визначення середнього (► п.9.44) й індивідуального (► п.9.45) значень результативної ознаки у її зв’язку з іншими, факторними, ознаками за очікуваних значень останніх. Прогноз виконується з використанням функціональних моделей тренду (► п.7.15) та регресії (► п.9.10) із значущими оцінками параметрів (► п.п.4.36, 7.16, 9.37) на певному рівні значущості t-критерію (► п.4.20). |
§ 4.4. Форми відображення статистичної інформації (► рис.4.2). Статистичні таблиці (► рис.4.3) та графіки (► рис.4.4) |
|
44. Статистична таблиця (► рис.4.3) |
Форма подання статистичних даних, як правило, результатів статистичного зведення; це – сукупність горизонтальних і вертикальних ліній, що перетинаються й утворюють по горизонталі рядки, а по вертикалі стовпчики (графи); перетин останніх – це клітинки, куди записують статистичні дані. Основні елементи таблиці – це підмет і присудок. Підмет статистичної таблиці – це групи та підгрупи досліджуваного явища (ознаки), що підлягають певній характеристиці за допомогою статистичних показників. Присудок статистичної таблиці – це показники, за допомогою яких відображають числові значення та характеристики досліджуваного явища (ознаки). Таблиці поділяють на (види статистичних таблиць): прості (облікові, територіальні, хронологічні) (► поз.3.1-5, з.№ №22, 23, 27, 29-31), групові (► з.№4), комбіновані (► з.№7). |
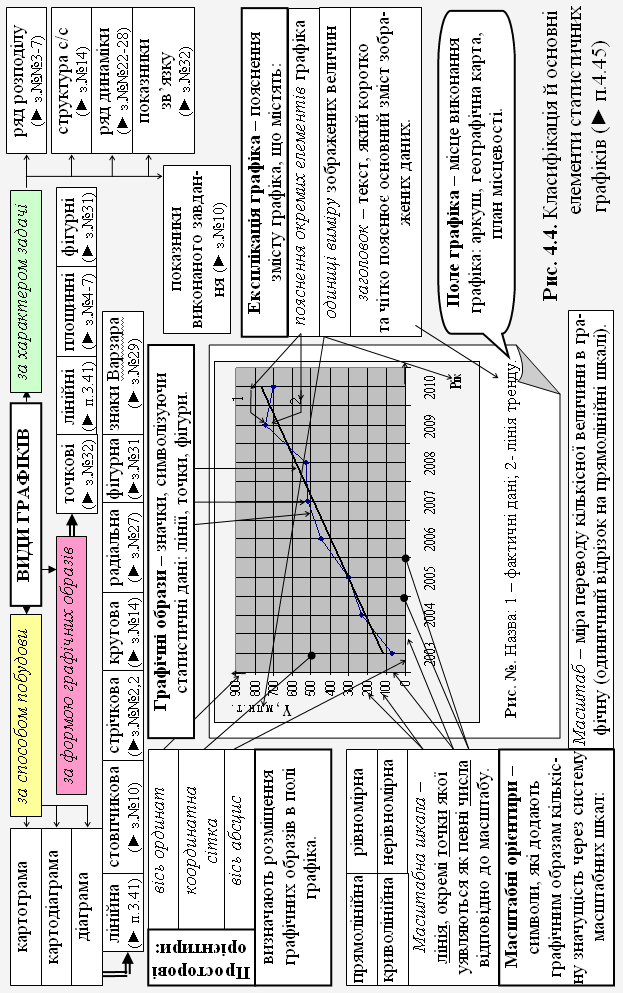
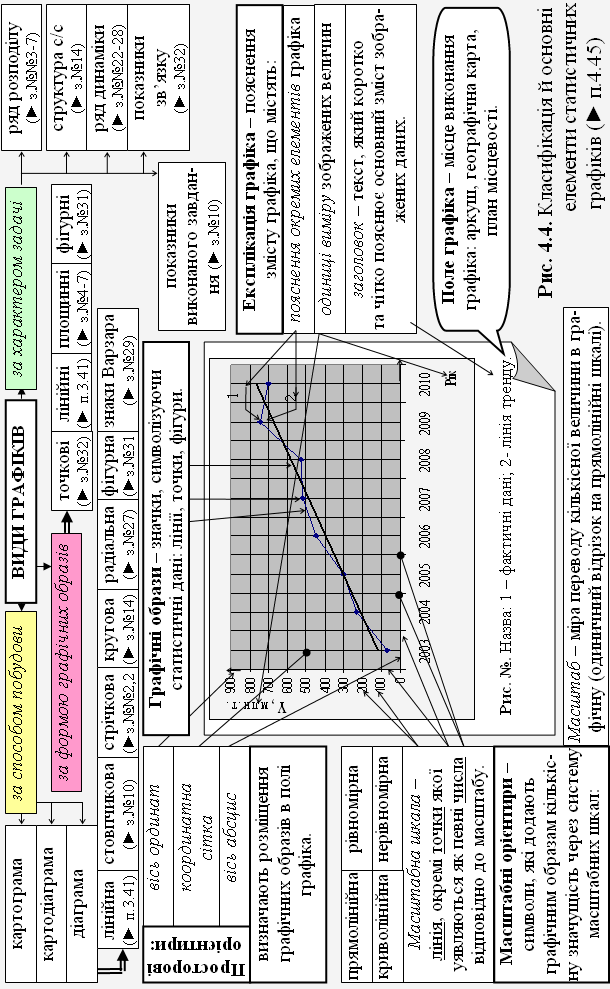
45. Статистичний графік (► рис.4.4) |
Форма подання статистичних даних, як правило, результатів статистичного зведення; це – малюнок, що зображає статистичні дані за допомогою умовних геометричних фігур (ліній, точок, інших знаків). Елементами графіків є: поле графіка, графічний образ, просторові та масштабні орієнтири, експлікація графіка. Графіки поділяють на (види статистичних графіків): а) за способом побудови: діаграми, картограми, картодіаграми; б) за формою графічних образів: точкові (► з.№32), лінійні (► п.3.41), площинні (► з.№№4-7), фігурні (► з.№31); в) за характером задач: ряд розподілу (► з.№№3-7), структура статистичної сукупності (► з.№14), ряд динаміки (► з.№№22-28), показники зв’язку (► з.№32), показники виконаного завдання (► з.№10). |
Продовження таблиці 4
1 |
2 |
45. Статистичний графік (продовження) |
Діаграми бувають (види): лінійними (► п.3.41), стовпчиковими (► з.№10), стрічковими (► з.№№2,29), круговими (► з.№14), радіальними (► з.№27), фігурними (► з.№31), знаками Варзара (► з.№29). |

 орми
орми

 теоретичні розподіли теорії ймовірностей
(► п.п.4.12-19)
теоретичні розподіли теорії ймовірностей
(► п.п.4.12-19)
 нтервал
нтервал
 математичної статистики (►
п.п.4.20-22)
математичної статистики (►
п.п.4.20-22)
 ибіркові
оцінки (►
п.п.4.24 і 6.10):
ибіркові
оцінки (►
п.п.4.24 і 6.10): статистика)
статистика)
 уассона
уассона


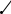


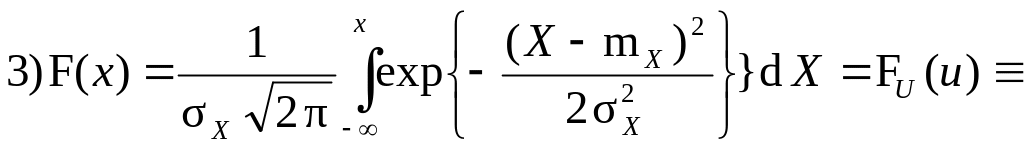
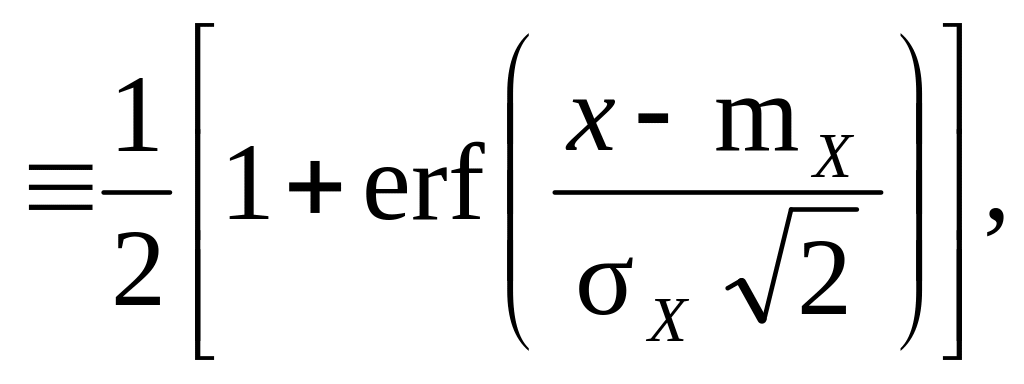 F(-∞)
→ 0,
F(+∞)
→ 1,
F(-∞)
→ 0,
F(+∞)
→ 1,
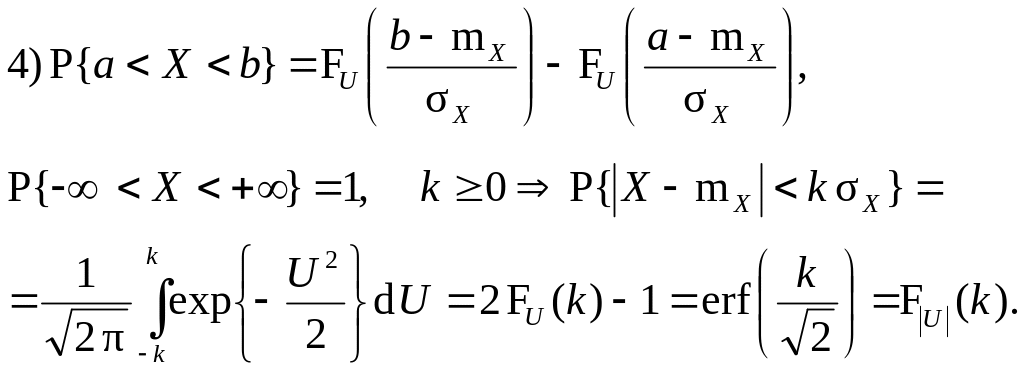

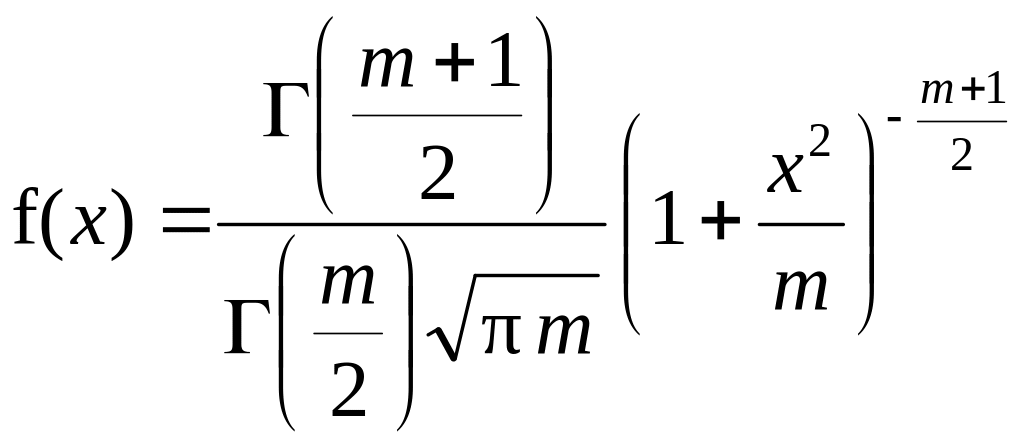 ,
,
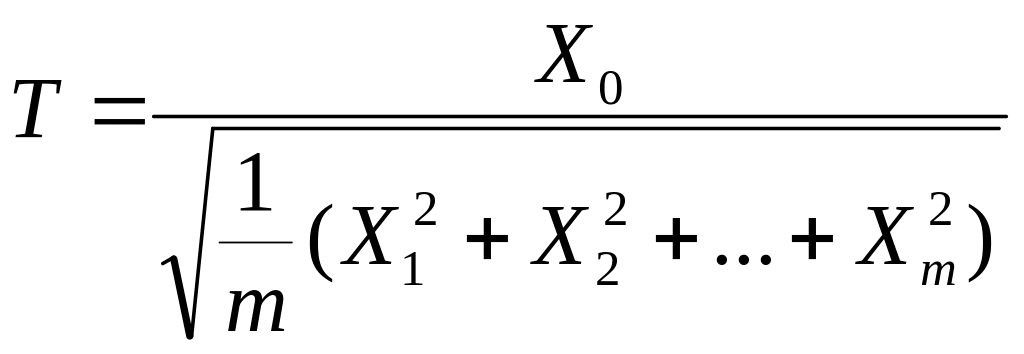
 П
П
 ірсона)
ірсона)
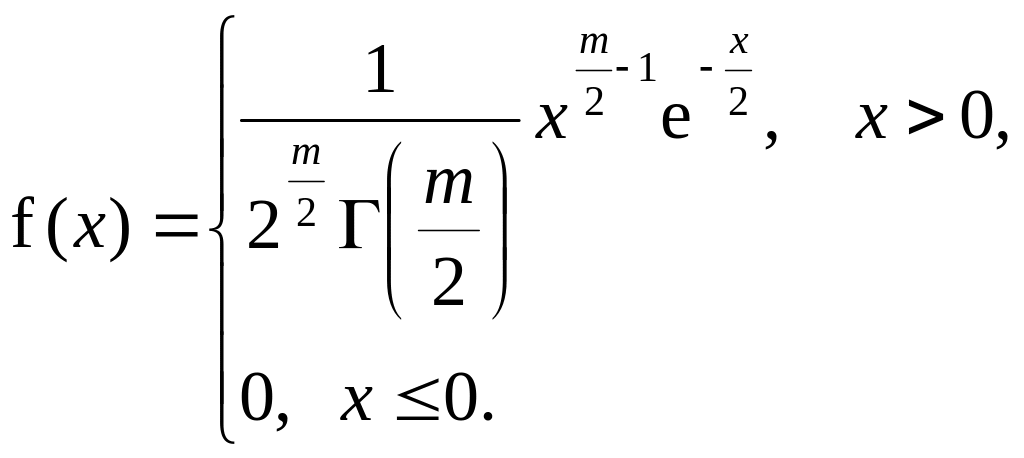

 Фішера)
Фішера)

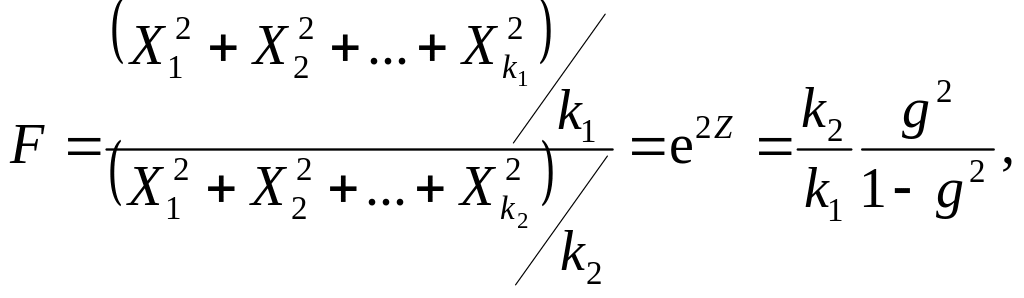
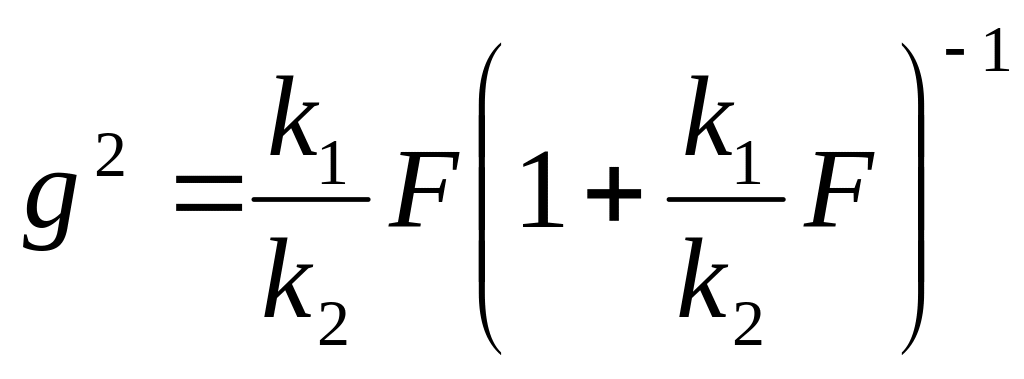
 ;
;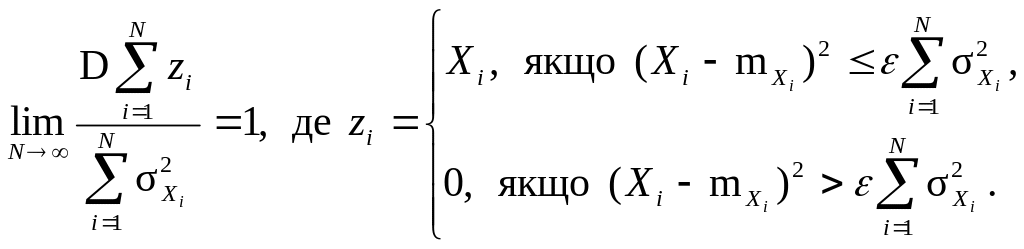

 2.
Критерій статистичної гіпотези
(продовження)
2.
Критерій статистичної гіпотези
(продовження)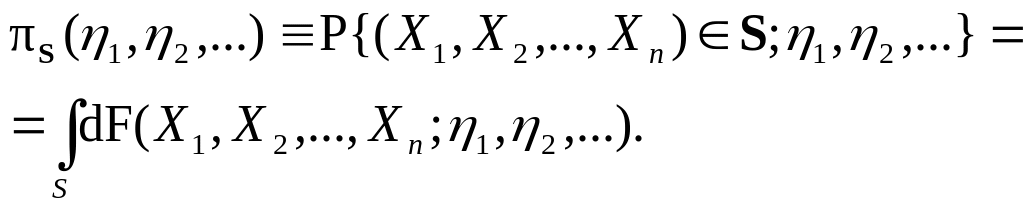




 область
S перевіряє
область
S перевіряє
 просту
гіпотезу на
просту
гіпотезу на