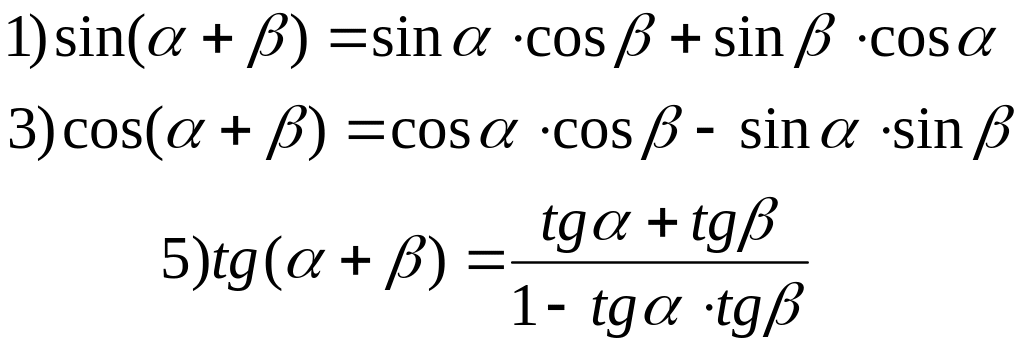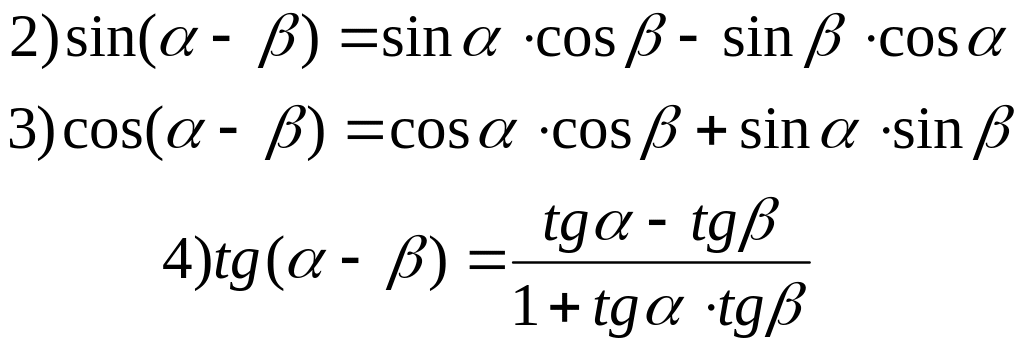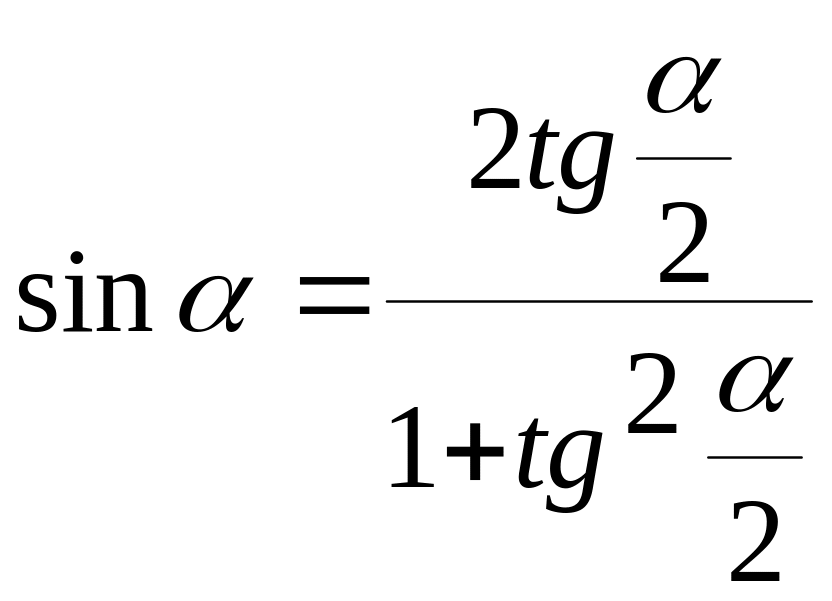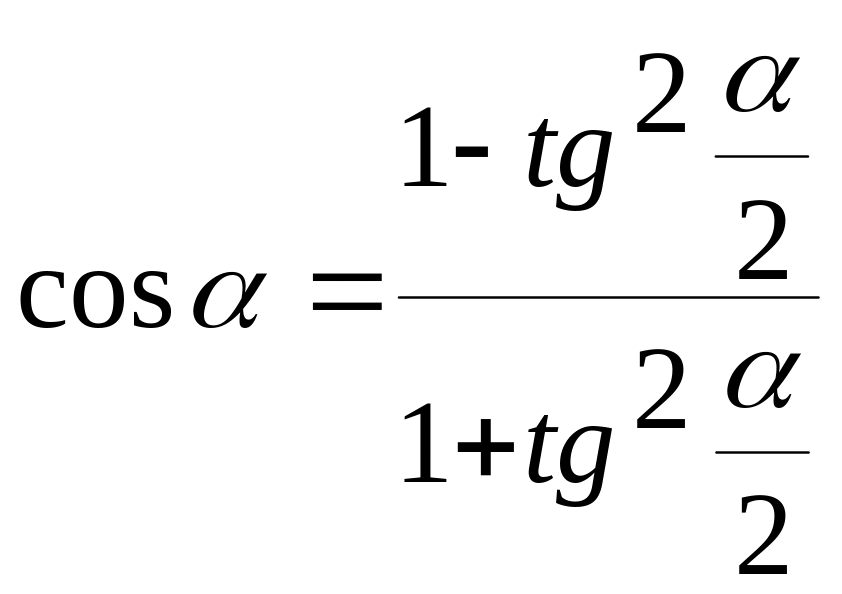- •Кафедра высшей и прикладной математики
- •Губкин 2009
- •Под редакцией в. В. Крутских
- •Справочный материал
- •1. Алгебра
- •1.1.Теория множеств
- •1.2. Действительные числа
- •1.3. Действия с дробями
- •1.4. Пропорция
- •1.5. Проценты
- •1.5. Погрешность вычислений
- •1.11. Определение логарифма
- •1.13. Свойства логарифмов
- •1.14. Логарифмирование и потенцирование
- •1.15. Теория многочленов
- •1.16. Выделение целой части из дроби
- •2. Алгебраические уравнения
- •2.1. Линейные уравнения
- •2.2. Квадратные уравнения
- •2.3. Выделение полного квадрата из квадратного трехчлена
- •2.4. Разложение квадратного трёхчлена на линейные множители
- •2.6. График квадратной функции
- •2.7. Рациональные уравнения
- •2.8. Уравнения с модулем
- •2.9. Кубические уравнения
- •2.9. Показательные уравнения
- •2.10. Логарифмические уравнения
- •3. Алгебраические неравенства
- •3.1. Линейные неравенства
- •3.2. Квадратные неравенства
- •Рациональные неравенства
- •3.5. Показательные неравенства
- •3.6. Логарифмические неравенства
- •3.7. Правила нахождения области определения и множества значений функции
- •4. Тригонометрия
- •5. Планиметрия
- •Треугольники
- •5.1. Косоугольный треугольник
- •5.3 Равнобедренный треугольник
- •Многоугольники
- •Четырехугольники
- •5.4. Параллелограмм
- •5.5. Прямоугольник
- •5.7. Квадрат
- •5.8. Трапеция
- •5.9. Окружность и круг
- •6. Стереометрия
- •Пирамида
- •Цилиндр
- •Сфера и шар
3.7. Правила нахождения области определения и множества значений функции
Область определения функции
|
(20) |
|
|
||
Множество значений функции
|
(21) |
|
Пример. Найти
область определения функции
![]() ,
,
![]()
►а)![]()
![]()
б)
![]()

Рисунок 11
![]() ◄
◄
4. Тригонометрия
4.1. Углы измеряются в градусах и радианах, соотношение между ними
1800=![]() радиан
радиан
Поэтому 10=![]() радиан и 1 радиан=
радиан и 1 радиан=![]() градусов.
градусов.
4.2. Угол, отложенный по часовой стрелке, считается отрицательным, а угол, отложенный против часовой стрелки, считается положительным.
Будем откладывать углы от положительного направления оси Ox.
4.3. Круг, с центром в начале координат и радиусом 1, называется единичным или тригонометрическим кругом.
4.4.
Каждому углу
соответствует точка
![]() ,
ее координаты называются соответственно
косинусом и синусом угла
:
,
ее координаты называются соответственно
косинусом и синусом угла
:
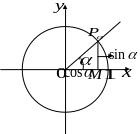
Рисунок 12
![]()
4.5. В прямоугольном треугольнике:
Синус угла есть отношение противолежащего катета к гипотенузе.
Косинус угла есть отношение прилежащего катета угла к гипотенузе.
Тангенс угла есть отношение противолежащего катета к прилежащему катету.
Котангенс угла есть отношение прилежащего катета к противолежащему катету.
4.6. Область определения тригонометрических функций
D
(![]() )=
)=![]() D
(
D
(![]() )=
)=
D (tg
):
![]() D (ctg
):
D (ctg
):
![]()
D
(tg
.ctg
):
![]()
4.7. Множество значений тригонометрических функций
![]() ,
т.е.
,
т.е.
![]()
![]() ,
т.е.
,
т.е.
![]()
![]()
![]()
4.8. Периодичность тригонометрических функций
и
есть периодические функции с наименьшим
периодом
![]() и
и
![]()
![]()
![]() и
и
![]() есть периодические функции с наименьшим
периодом
есть периодические функции с наименьшим
периодом
![]() и
и
![]()
![]()
4.9. Знаки тригонометрических функций
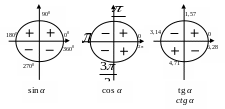
Рисунок 13
4.10. Четность тригонометрических функций
![]() — функция четная
— функция четная
![]() — функция нечетная
— функция нечетная
![]() —
функция нечетная
—
функция нечетная
![]() —
функция нечетная
—
функция нечетная
4.11.Формулы
приведения.
Они позволяют отбросить числа
![]() ,
пользуясь двумя правилами:
,
пользуясь двумя правилами:
находим четверть, в которой расположен угол, и определяем знак приводимой функции в этой четверти и ставим его перед приведенной функцией;
меняем функцию на кофункцию, если аргументом являются углы
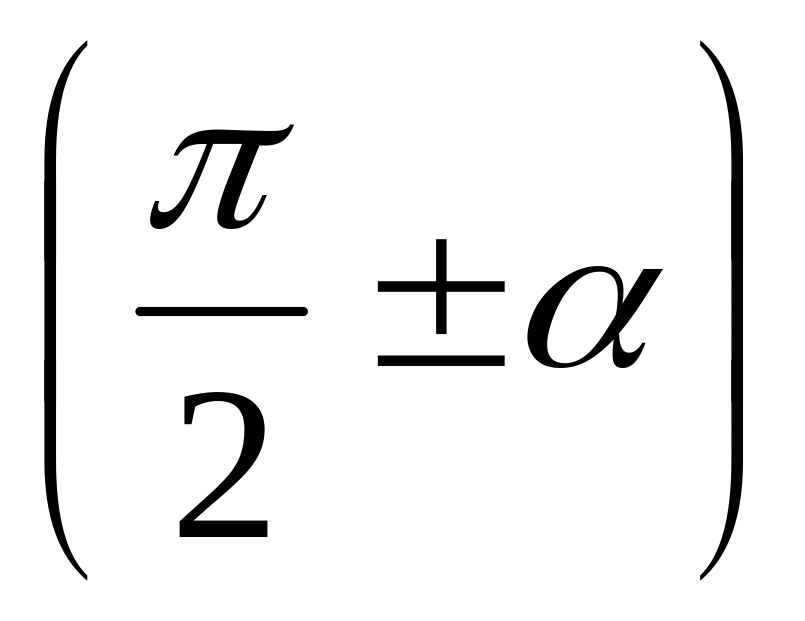 или
или
 ,
т.е. если отбрасываем угол
,
т.е. если отбрасываем угол
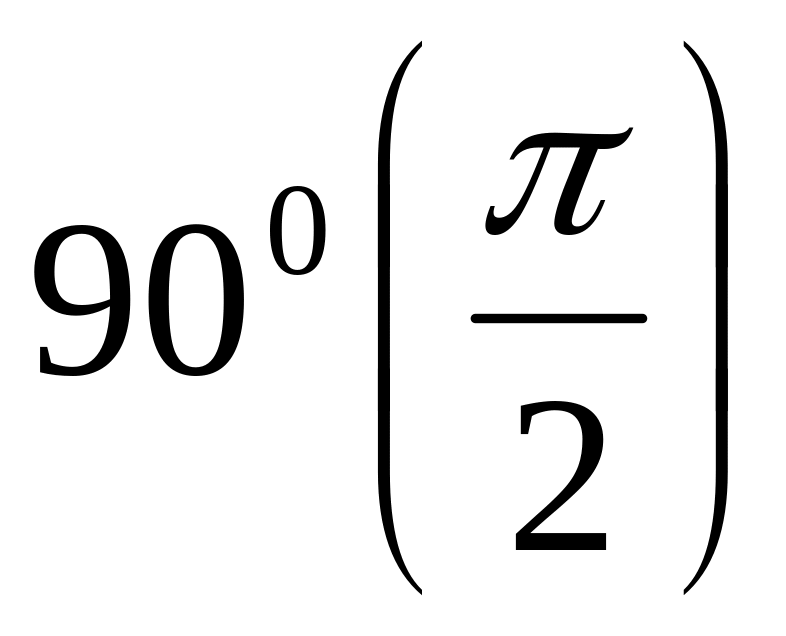 или
или
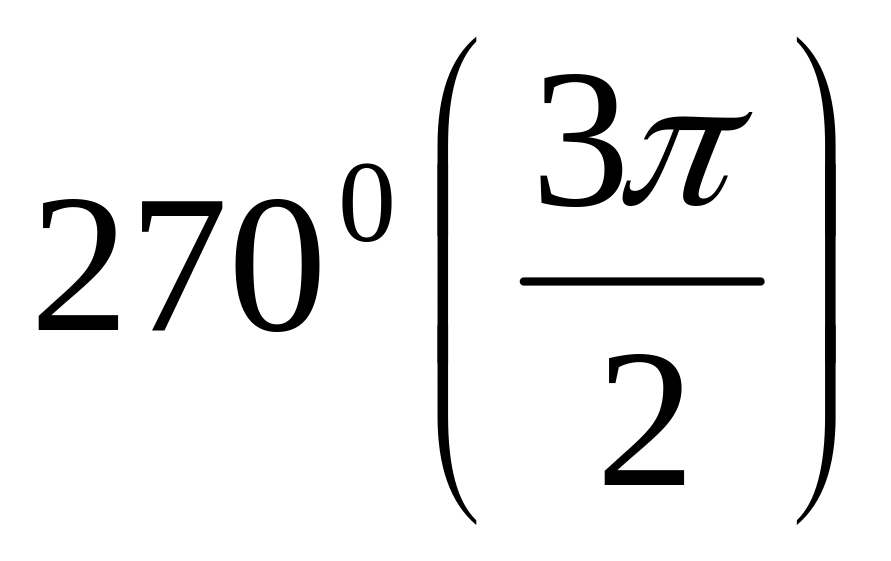 ;
;не меняем название функции, если аргументом являются углы
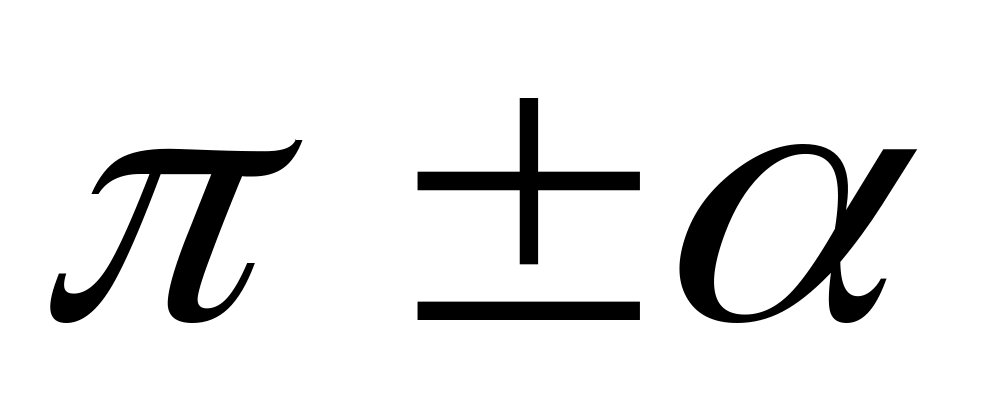 или
или
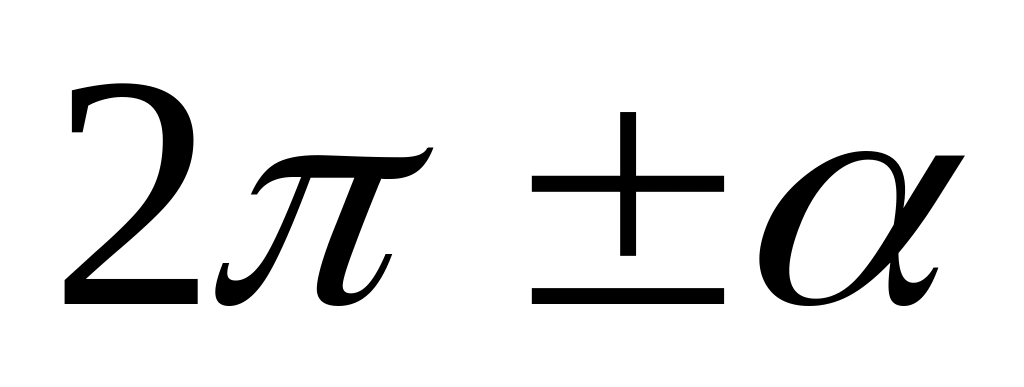 ,
т.е. если отбрасываем угол
,
т.е. если отбрасываем угол
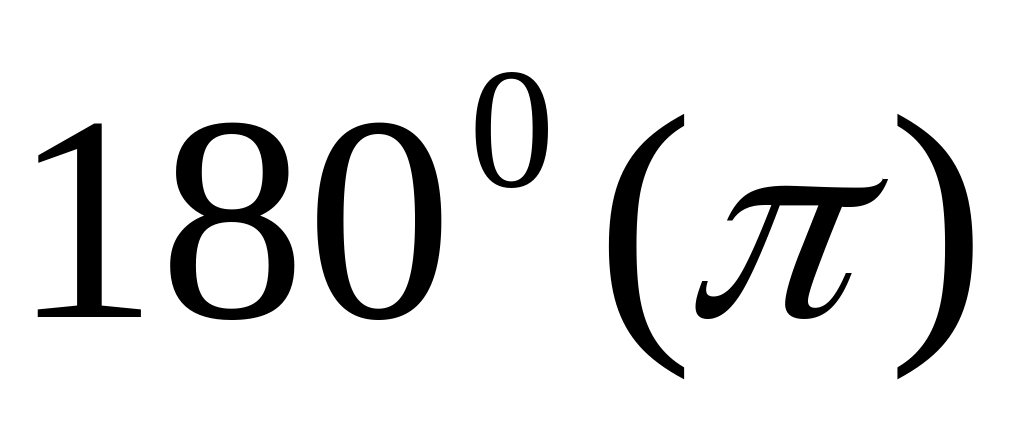 или
или
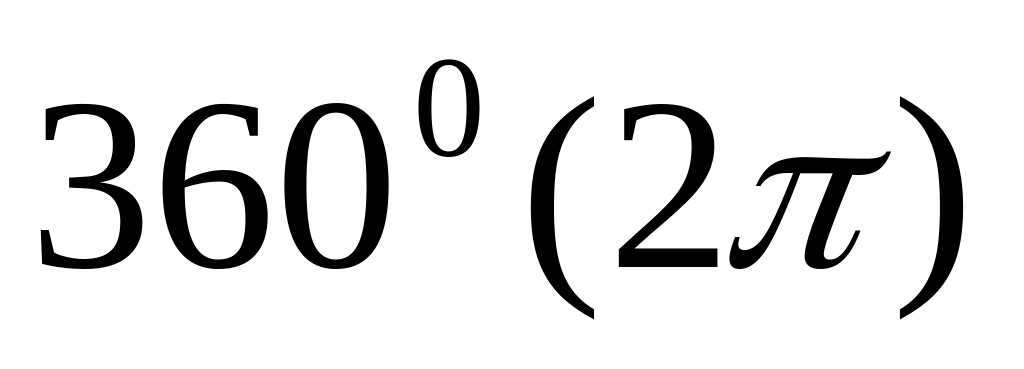 .
.
4.12. Тригонометрические функции одного и того же угла.

4.13. Формулы сложения
|
|
4.14. Формулы двойных углов
1). sin2α = 2 sin α cos α |
1а). sin α cos α
=
|
1б). sin2 α cos2 α
=
|
2). cos2α = cos2α – sin2α |
3). tg2α = |
3). сtg2α = |
4.15. Выражения тригонометрических функций через косинус двойного угла (формулы понижения степени)
1).
|
1а)
|
1б)
|
|
2)
|
2а) |
2б)
|
|
3)
|
4)
|
||
4.16. Выражение тригонометрических функций через тангенс половинного угла (универсальная подстановка)
1)
|
2) |
3) |
4.17. Преобразование суммы тригонометрических функций в произведение
1) sin α +sin β = |
2)
sin α -sin β = |
3)cos α + cos β = |
4) cos α – cos β
= |
5) |
6) |
4.18. Преобразование произведения тригонометрических функций в сумму
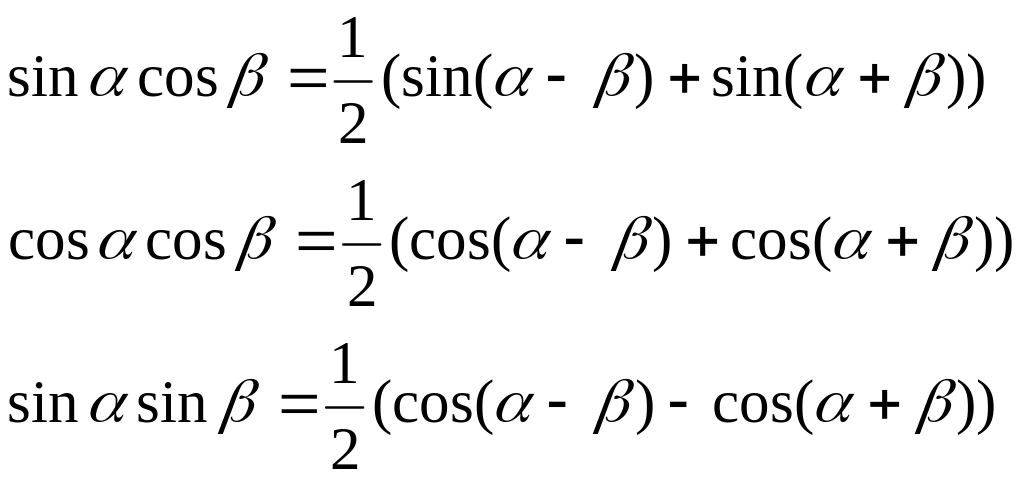
4.19. Обратные тригонометрические функции
![]()
![]()
![]()
![]()
Формулы решения простейших тригонометрических уравнений
|
|
|
|
|
a |
где |a|<1,
|
где |a|<1, |
|
|
a=0 |
|
|
, |
, |
a=1 |
|
|
|
, |
a=-1 |
|
|
|
|
4.21. Таблица значений тригонометрических функций некоторых углов
α |
00 |
300 |
450 |
600 |
900 |
1800 |
2700 |
3600 |
0 |
|
|
|
|
|
|
|
|
sinα |
0 |
|
|
|
1 |
0 |
-1 |
0 |
cosα |
1 |
|
|
|
0 |
-1 |
0 |
1 |
tgα |
0 |
|
1 |
|
|
0 |
- |
0 |
ctgα |
|
|
1 |
|
0 |
- |
0 |
|