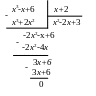1.11. Определение логарифма

1⁰. Логарифмом числа b по основанию b называется показатель степени, в которую нужно возвести число a, чтобы получить b, обозначается и

2⁰. Десятичный логарифм — это логарифм по основанию 10: .

3⁰. Натуральный логарифм — это логарифм по основанию : .

1.12. Основное логарифмическое тождество:

(2)

Например,

1.13. Свойства логарифмов

1. Сумма логарифмов есть логарифм произведения

2. Разность логарифмов есть логарифм дроби

3. Число, стоящее перед логарифмом ставим в показатель степени выражения, стоящего после знака логарифма

4. Переход к новому основанию

Следствия:

5.

6.

7.

8.

9. Любое число представимо в виде логарифма

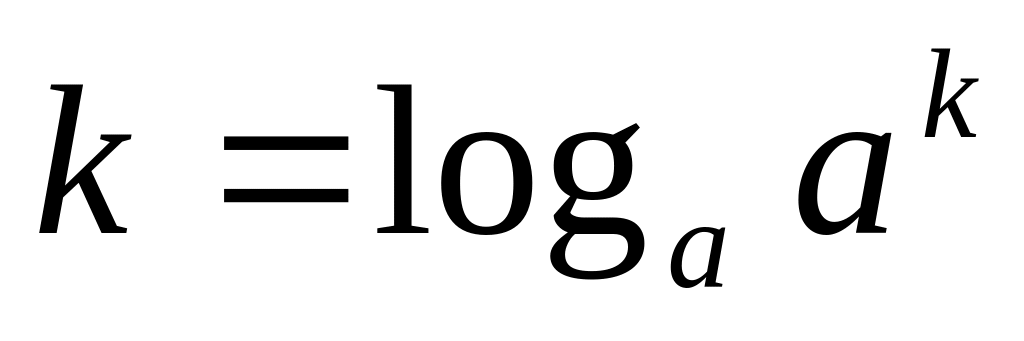
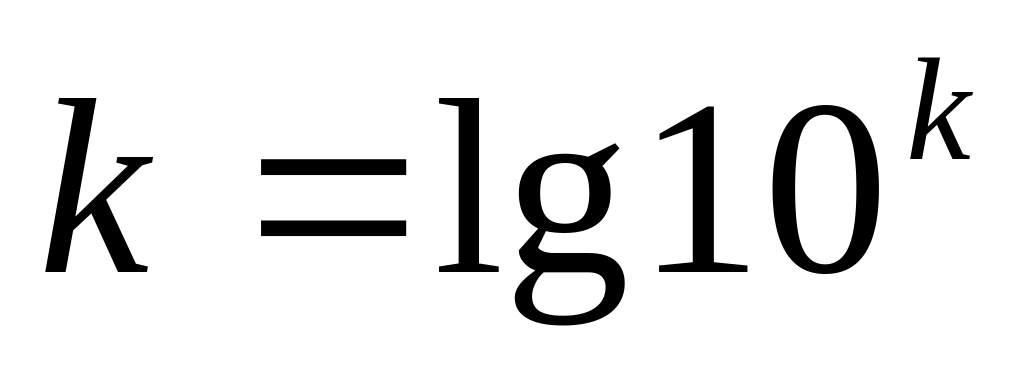
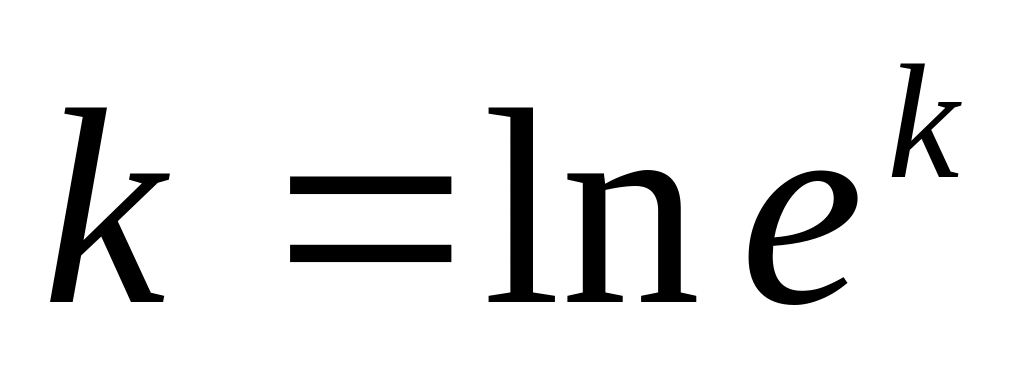
10. Любое число k>0 представимо в виде степени

Пример. Вычислить a) если ; б)

►а) перейдём в к основанию 2. Воспользуемся свойством 4:

.

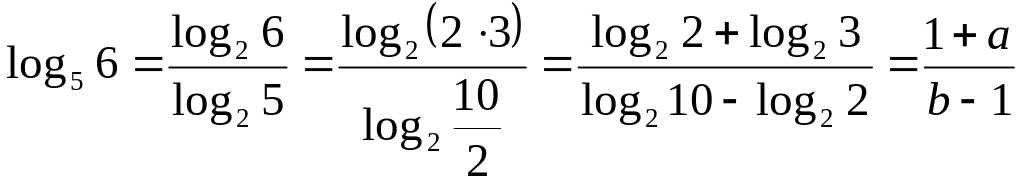б) заменим корни степенями и воспользуемся свойством 6:

.◄

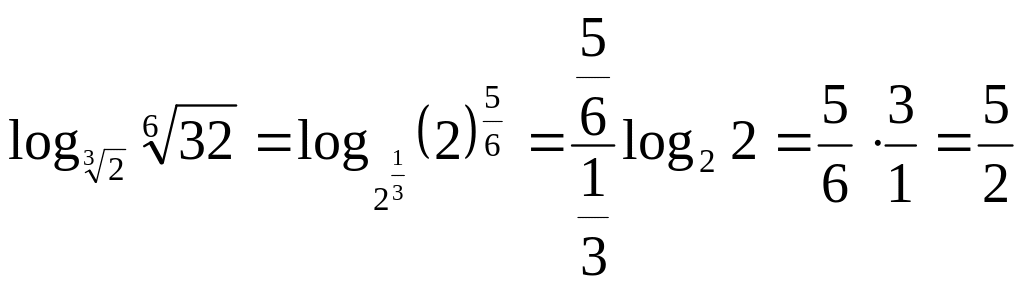1.14. Логарифмирование и потенцирование

Если некоторое выражение составлено из положительных чисел с помощью операций умножения, деления и возведение в степень, то, используя свойства логарифмов, можно выразить через логарифмы входящих в выражение чисел. Такое преобразование называется логарифмированием. Обратная задача: нахождение выражения по его логарифму, называется потенцированием.

Пример 1. Прологарифмировать по основанию выражение .

► ◄

Пример 2. Найти , если

► ◄

1.15. Теория многочленов

Многочленом степени называется целая рациональная функция

(3)

Многочлен - степени
Многочлен - степени
Многочлен - степени
Многочлен - степени
Многочлен - степени

Например, есть многочлен - степени, 2 есть многочлен - степени.

Деление многочленов:

1.16. Выделение целой части из дроби

Дробь называется неправильной, если в числителе стоит многочлен степени не ниже степени многочлена знаменателя.

Тогда дробь можно представить в виде: , где — частное от деления на (целая часть), — полученный при этом остаток.

Пример. Выделить целую часть из дроби .

►Дробь неправильная, делим числитель на знаменатель столбиком:

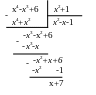
Целая часть (под уголком), а остаток (в конце деления). Поэтому дробь будет иметь вид:

◄

2. Алгебраические уравнения