Динамическая модель Леонтьева

Так как мы рассмотрели продуктивную модель межотраслевого баланса безотносительно ко времени, т.е. все ее компоненты полагались осредненными за некоторый временной интервал и «одномоментными». В реальности продукт, предназначенный для внутреннего и конечного потребления в период , определяется не текущим выпуском, а выпуском в последующий период . Эта задержка производства обусловлена многими факторами, в частности инерцией планирования и перенастройки, мобилизацией внутренних ресурсов и изменение транспорта сырья и т.д.

С учетом этого система уравнений баланса, в предположении о постоянстве доли внутреннего потребления каждой отраслью, будет иметь следующий вид

(32)

Соотношения (32) составляют систему линейных разностных уравнений первого порядка с постоянными коэффициентами .

Как и прежде, введем вектор валового выпуска , матрицу прямых затрат и вектор конечного потребления . Тогда систему (32) можно переписать в матричной форме:

. (33)

Теперь задача формулируется следующим образом: при заданном векторе конечного потребления и матрице определить динамику (изменение во времени) вектора валового выпуска .

Одна из основных задач прогноза с использованием динамической модели Леонтьева такова: известны динамика вектора конечного потребления и вектор валового выпуска в начальный момент времени ; требуется рассчитать вектор валового выпуска на момент времени . Эту задачу можно решить при помощи формулы:

. (33)

Пример 2. Обратимся к данным табл. 1. Пусть известны продуктивная матрица , а также заданные в момент времени векторы валового выпуска и , указанные в этой таблице:

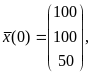
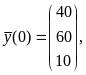
Требуется рассчитать вектор валового выпуска на момент времени , если все компоненты вектора конечного потребления увеличиваются на за каждый период.

Решение. Вектор конечного потребления, согласно условию задачи, имеет вид

.

Применяя формулу (33), получаем .

Теперь нужно вычислить матрицу изменяя состояния и вектор и подставить их в это уравнение. Выполняя указанные действия, получим решение поставленной задачи:

.

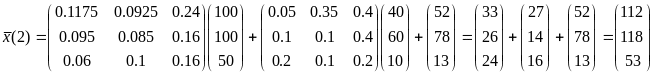Таким образом, при указанном темпе роста продукта конечного потребления необходимо через два временных цикла увеличить компоненты валового выпуска соответственно на , и по сравнению с исходными величинами на начальный момент времени.

Список литературы:

1. А. С. Солодовников, В. А. Бабайцев, А. В. Браилов – Математика в экономике - М: Финансы и статистика, 1999

2. М. С. Красс – Математика для экономических специальностей – М: ИНФРА – М., 1999

3. Математика в экономике: Учебно-методическое пособие // Под редакцией Н. Ш. Кремера – М: Финстатинформ, 1999