Паутинные модели рынка
Свойство
непрерывной функции (теорема о
существовании корня) находит неожиданное
применение в математических моделях
рынка. Как известно, две основные
категории рыночных отношений – спрос
и предложение. И то и другое зависят от
многих факторов, среди которых главный
– это цена товара. Обозначим цену товара
,
объем спроса
,
величину предложения
.
При малых
имеем
(спрос превышает предложение), при
больших
,
наоборот,
.
Считая
и
непрерывными функциями, приходим к
заключению, что существует такая цена
,
для которой
,
т.е. равен спрос равен предложению. Цена
называется равновесной, спрос и
предложение при этой цене также
называются равновесными.
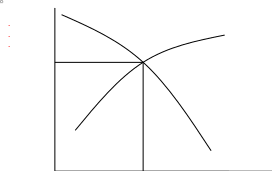
Установление равновесной цены – одна из главных задач рынка. Рассмотрим простую модель поиска равновесной цены – так называемую паутинную модель. Она объясняет феномен регулярно повторяющихся циклов изменения объемов продажи и цен.
Предположим, что решение о величине объема производства принимается в зависимости от цены товара в предыдущий период времени.
Рассмотрим ситуацию, изображенную на рис. 3.
Пусть
в начальной точке предложение товара
имеет значение
и выбрано так в зависимости от цены
товара
в предыдущий период. Поскольку эта цена
больше равновесной, то на кривой спроса
ей соответствует объем покупок
.
Производителю, исходя из такой информации
о состоянии рынка, приходится опустить
цену товара до величины
.
Цена
ниже равновесной, поэтому на рынке
увеличивается спрос до величины
.
На кривой предложения
этой величине соответствует цена
предложения
и т.д. В этом случае спираль сходится к
точке рыночного равновесия
.
Рис. 3
Впрочем, описанная «спираль» не всегда «скручивается». В некоторых случаях она может и «раскручиваться», как показывает, например, рис. 4.
От каких свойств функций и зависит сходимость или расходимость описанной выше «спирали»? Этот вопрос очень сложен. Поэтому, укажем лишь один фактор, влияющий на сходимость – эластичность (спроса, соответственно, предложения).
Рис. 4.
Модель Леонтьева многоотраслевой экономики
Макроэкономика функционирования многоотраслевого хозяйства требует баланса между отдельными отраслями. Каждая отрасль, с одной стороны, является производителем, а с другой – потребителем продукции, выпускаемой другими отраслями. Возникает довольно не простая задача расчета связи между отраслями через выпуск и потребление продукции разного вида. Впервые эта проблема была сформулирована в виде математической модели в трудах известного американского экономиста В. Леонтьева в 1936 году, который попытался проанализировать причины экономической депрессии США 1929-1932 гг. Эта модель основана на алгебре матриц и используют аппарат матричного анализа.