
- •Лекционный материал (математическое моделирование)
- •1. Основные предположения о гравитационном режиме течения грунтовых вод
- •2. Баланс массы в элементе грунта.
- •3. Замыкание закона сохранения массы.
- •4. О некоторых свойствах уравнения Буссинеска.
- •5. Основные выводы.
- •Сохранение энергии
- •1. Предварительные сведения о процессах теплопередачи.
- •2. Вывод закона Фурье из молекулярно-кинетических представлений.
- •3. Уравнение баланса тепла.
- •4. Постановка типичных краевых условий для уравнения теплопроводности.
- •5. Об особенностях моделей теплопередачи.
5. Об особенностях моделей теплопередачи.
Наиболее простая из всех обсуждаемых выше задач теплопроводности – задача о стационарном процессе для уравнения (11) на отрезке :
 ,
,
 ,
,
 .
.
Ее решение – линейная функция координаты :
 ,
. (19)
,
. (19)
Решение (19) имеет вполне очевидный физический смысл. Действительно, при стационарном процессе потоки тепла, входящие в любое поперечное сечение стержня и выходящие из него, равны (иначе температура в сечении менялась бы).
Поэтому
поток должен быть постоянен в любой
точке
,
что по закону Фурье (3) при
 возможно
лишь при линейном «профиле» температуры.
Вместе с тем, применение закона Фурье
приводит к появлению одного не имеющегося
физического смысла эффекта, характерного
для уравнений параболического типа.
возможно
лишь при линейном «профиле» температуры.
Вместе с тем, применение закона Фурье
приводит к появлению одного не имеющегося
физического смысла эффекта, характерного
для уравнений параболического типа.
Поясним
его, рассмотрев для уравнения (11),
решаемого во всем пространстве
,
задачу о так называемом мгновенном
точечном источнике тепла.
Требуется найти распределение температуры
при всех
,
,
вызванное выделение в момент
в
плоскости
 некоторого
количества тепла
некоторого
количества тепла
 .
Начальная температуры считается равной
нулю:
.
Начальная температуры считается равной
нулю:
 ,
.
,
.
Такая постановка – идеализация реального процесса, справедливая при выполнении соответствующих условий (например, по центру холодного стержня пропускается мощный поперечный импульс электрического тока, действующего очень короткое время и затрагивающего малый участок металла). Решение поставленной таким образом задачи дается формулой:
 ,
,
,
,
 , (20)
, (20)
что проверяется непосредственной подстановкой в уравнение (11).
Симметричная функция (20) в силу известного равенства
 ,
,
обладает свойством
 .
,
.
,
так что закон сохранения энергии выполняется.
В
то же время, согласно (20) температура в
любом точке пространства в любой момент
отлична
от нуля. Тем самым, модель (11) и многие
другие модели теплопередачи описывают
процессы с бесконечной скоростью
распространения возмущений (температура
при
была
нулевой для
).
Этого недостатка лишены (но лишь при
определенных условиях) уравнения типа
нелинейной теплопроводности (10) (в
частности уравнение (13)). Для модели (10)
с
 ,
рассмотрим
процесс распространения тепла в
полупространстве
при
заданной на границе температуре:
.
Начальная температура среды считается
ненулевой:
,
,
рассмотрим
процесс распространения тепла в
полупространстве
при
заданной на границе температуре:
.
Начальная температура среды считается
ненулевой:
,
 .
.
Частное решение этой задачи, отвечающее граничному закону
 ,
,
,
,
Имеет
вид бегущей волны, распространяющейся
от границы вглубь вещества не с
бесконечной, а с конечной скоростью
 (рис. 5.1):
(рис. 5.1):
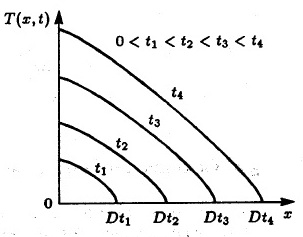
Рис. 5.1
 ,
. (21)
,
. (21)
Однако это свойство реализуется лишь при распространении тепла в холодную среду и теряется в случае отличной от нуля начальной температуры вещества. Описанный дефект, связанной с неприменимостью закона Фурье (и закона Дарси в случае уравнения Буссинеска) в окрестности фронта распространения тепловой энергии, не препятствует широкому применению параболических уравнений (из (20) видно, что доля энергии, содержащейся в веществе при достаточно больших значениях , ничтожна мала в сравнении с полной энергией ). Они служат хорошим примером универсальности математических моделей, описывая большое количество разнообразных процессов.
