Упрощенный пример

На рис. 6 - За представлены обычное и предельное время и издержки для каждой операции, рассчитанная наклонная и предел сокращения вре­мени, общие прямые издержки и схема проекта продолжительностью в 25 единиц времени.

Операция	Наклон	Максимально предельное время	Прямые издержки
			Нормальные		Срочные
			Время	Стоимость	Время	Стоимость
А	20	1	3	$50	2	$70
В	40	2	6	80	4	160
С	30	1	10	60	9	90
D	25	4	11	50	7	150
Е	30	2	8	100	6	160
F	30	1	5	40	4	70
G	0	0	6	70	6	70

Общие прямые издержки $ 450

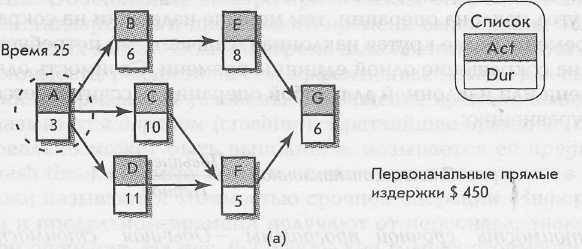
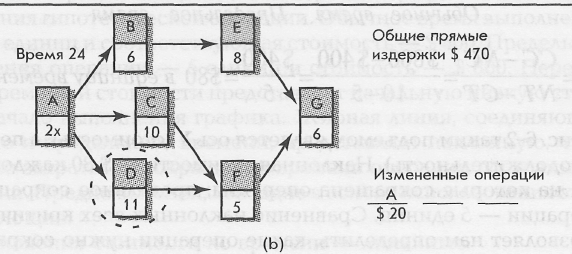
Рис. 6-3. Пример альтернативной стоимости времени

Отметим, что общие прямые издержки для периода, продолжительно­стью в 25 единиц — $450. Это важная точка для начала процедуры сокра­щения времени критического пути и нахождения общих прямых издержек для каждой конкретной операции продолжительностью меньше чем 5 единиц. Максимальное время, на которое операция может быть сокращена, представляет разницу между обычным и предельным временем выполнения операции. Например, операция D может быть сокращена с обычной продолжительности в 11 единиц времени до предельного времени 7 единиц, или максимально на 4 единицы времени. Положительная наклонная для операции D рассчитывается следующим образом:

Наклон = (Стоимость срочной программы - Обычная стоимость) / (Обычное время - Предельное время) =

= ($ 150 - $ 50) / (11 – 7) = $ 100 / 4 = $ 25 за сокращенный период времени

На схеме видно, что критический путь представлен операциями А, D, F, G. Так как невозможно сократить операцию G, операция А обведенa кружком, поскольку является наименее дорогой; то есть ее наклонная ($ 20) меньше, чем наклонные операций D и F ($ 25 и $ 30). Сокращение операции А на одну единицу времени сокращает продолжительность проекта до 24 единиц времени, но увеличивает общие прямые издержки до $ 470 ($ 450 + $ 20 = $ 470). Рис. 6 - Зв отражает эти изменения. Продол­жительность операции А сократилась до двух единиц времени; «х» пока­зывает, что операция не может больше сокращаться. Операция D обве­дена потому, что она наименее дорогая ($ 25), чтобы сократить время проекта до 23 единиц времени. Сравните стоимость операции F. Общие прямые издержки проекта продолжительностью в 23 единицы времени составят $ 495 (см. рис. 6 - 4а).

Обратите внимание, что схема проекта на рис. 6-4а теперь имеет два критических пути— A, C, F, G и A, D, F, G. Сокращение продолжительности проекта до 22 единиц времени потребует сокращения продолжительности операции F, поэтому она обведена. Эти изменения показаны на рис. 6 - 4в. Общие прямые издержки для продолжительности в 22 единицы времени составят $ 525. Это сокращение приведет к возникновению третьего кри­тического пути — A, B, E, G; все операции критические. Наименее дорогостоящим методом сокращения продолжительности проекта до 21 единицы времени является комбинация обведенных операций C, D, E, стоимость которых соответственно $ 30, $ 25, $ 30, и увеличение общих прямых издер­жек до $ 610.

Результаты этих изменений отражены на рис. 6 - 4с. Хотя некоторые операции все еще можно сократить (те, которые не имеют «х» у времени операции), ни одна операция или их комбинация не приведут к сокраще­нию продолжительности проекта.

Имея общие прямые издержки для множества конкретных продолжительностей выполнения проекта, следующий шаг, который нужно сделать, — это собрать косвенные издержки для различных продолжительностей. Эти издержки обычно представляют ежедневную ставку и их легко получить в бухгалтерии. В табл. 6 - 1 представлены общие прямые издержки, общие косвенные издержки и общие издержки проекта.

Те же издержки внесены в рис. 6 - 5. На этом графике показано, что оптимальная стоимость продолжительности в 22 единицы времени — $ 775.

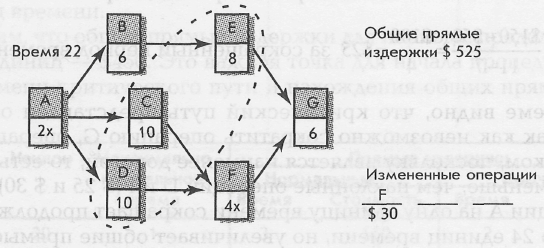
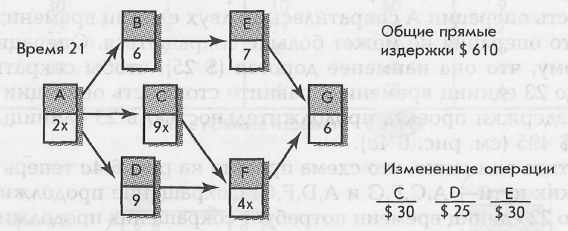
Рис. 6-4. Пример альтернативной стоимости времени (продолжение)

Таблица 6-1. СУММА ИЗДЕРЖЕК ПО ПРОДОЛЖИТЕЛЬНОСТИ

Продолжительность проекта	Прямые издержки	Косвенные издержки	Общие издержки
25	450	400	$ 850
24	470	350	820
23	495	300	795
22	525	250	775
21	610	200	810

Предположим, что проект будет реализован, как планировалось, тогда любое отклонение от времени продолжительности увеличит издержки проекта. Отклонение от 25 до 22 происходит потому, что в этом диапазоне угол наклона косвенных издержек больше, чем угол наклона прямых издержек.

ПРАКТИЧЕСКИЕ СООБРАЖЕНИЯ

Предельное время

Собрать информацию о предельном времени даже для проекта среднего размера достаточно трудно. Трудно объяснить, что означает предельное время. Что значит определение предельного времени как «минимального времени, в течение которого вы можете реально выполнить операцию»? Предельное время интерпретируют и понимают по-разному.

Те, кто занимается оценкой времени, чувствуют неуверенность, когда называют предельное время. Точность предельного времени и издержки в лучшем случае весьма приблизительны по сравнению с обычным временем и затратами.

Расчет времени срочных операций

Иногда стратегия «поживем - увидим» является мудрым решением. Срочное выполнение критической операции на раннем этапе осуществления проекта может привести к неэффективной трате денег, если дру­гая критическая операция завершена раньше или некритический путь становится новым критическим путем. В таких случаях рано потраченные деньги пропадают впустую, и нет никакой пользы от раннего завер­шения срочной операции. И наоборот, может иметь смысл срочно вы­полнить раннюю критическую операцию, если последующие операции, скорее всего, будут задерживаться и потребуют выигранного времени. Тогда у менеджера будет только один выход: аврально закончить последнюю операцию, чтобы снова войти в график. В конечном счете расчет времени срочных операций — это предварительная оценка, требующая тщательного рассмотрения имеющихся выборов, риска и важности выполнения операции в срок.

Рис. 6 - 5. График стоимости времени проекта

Линейность предположений

Поскольку точность сжатых сроков операции и издержки вызыва­ют сомнение, некоторые теоретики озабочены тем, что отношения вре­мени и затрат не линейные, а криволинейные, что редко заботит прак­тиков. Обоснованные и быстрые сравнения можно сделать, используя линейные предположения. Этот простой метод подходит для большин­ства проектов. Лишь в редких случаях, когда проекты крупные, слож­ные, с большой продолжительностью, может быть весьма полезным ис­пользование метода приведенной стоимости, что не входит в задачи этой книги.

Компьютерные решения

Не следует слишком сильно полагаться на компьютерные решения, которые не учитывают факторов неопределенности или риска. Некото­рые критические операции можно срочно выполнить без всякого риска, если что-то пойдет не так, как планировалось. Компьютерные решения свя­заны только с построением наклонных. Кроме того, в крупных комплекс­ных системах проекта сбор данных может оказаться чрезмерным и доро­гостоящим. В таких случаях общие собрания основных менеджеров про­екта помогут определить небольшие сегменты проекта, в которых существуют наибольшие возможности для сокращения времени критичес­кого пути при относительно низких затратах. Компьютер можно исполь­зовать для разработки графика стоимости времени для этого сегмента. Использование предложенного формального подхода дает возможность включить в анализ косвенные (накладные) расходы. Некоторые руководи­тели проектов не умеют учитывать косвенные расходы в ситуациях сокра­щения сроков проекта.