5 Завдання

5.1 Провести вимірювання та розрахунки необхідні для визначення об’єму тіл циліндричної форми.

5.2 Написати висновки та відповісти на контрольні запитання.

6 Питання вхідного контролю

6.1 Як побудовано штангенциркуль і як ним робити вимірювання?

6.2 Як побудовано мікрометр і як ним робити вимірювання?

6.3 Що називається відносною похибкою?

6.4 Як побудовано штангенциркуль і як ним робити вимірювання?

6.5 Як побудовано мікрометр і як ним робити вимірювання?

7 Хід роботи

7.1 Підготувати до виконання роботи протокол (див. Додаток): записати тему роботи, мету, оформити домашнє завдання тощо.

7.2 Вивчити будову вимірювальних приладів і їхні дані занести в таблицю приладів протоколу.

7.3 Визначити діаметр d і висоту h циліндра, виконавши по п'ять вимірювань (n = 5) кожної величини. Отримані дані внести в таблицю вимірювань протоколу.

7.4 Статистично обробити результати прямих вимірювань :

Обчислити середні арифметичні значення величин .

Обчислити відхилення від середнього кожного вимірювання Δd_i і Δh_i

Піднести їх до квадрата і просумувати для кожної величини окремо, одержавши

За заданими викладачем надійністю α і числом вимірювань n = 5 визначити коефіцієнт Стьюдента .

За формулою Стьюдента розрахувати абсолютну похибку обох величин Δd і Δh .

Розрахувати відносні похибки

Записати остаточний результат у вигляді чисельних значень величин, правильно виконавши округлення цих величин: ;

7.5. Обчислити середнє значення об’єму циліндра V~ (зробити непряме вимірювання об’єму).

7.6. Обчислити відносну і абсолютну ΔV похибки непрямого вимірювання об’єму:

Вивести формулу розрахунку відносної похибки об’єму .

Обчислити відносну похибку об’єму циліндра за відомими похибками діаметра і висоти.

Обчислити абсолютну похибку вимірювання об’єму ΔV.

7.7. Записати остаточний результат у вигляді чисельних значень величин, правильно виконавши округлення величин: ;

7.8. Остаточно оформити протокол виконання роботи: записати висновок, підписати протокол (див. Додаток до даних методичних вказівок) і дати на підпис викладачеві.

8 Питання вихідного контролю

8.1 Як розрахувати абсолютну і відносну похибки прямих вимірювань?

8.2 Як розрахувати абсолютну і відносну похибки непрямих вимірювань?

8.3 Основні правила округлення похибок і середніх значень вимірюваних величин.

9 Перелік посилань

9.1 Кальнев Н.А. Методические указания по курсу физики "Механика". Одесса: ОЭИС, 1991.

9.2 Трофимова Т.И. Курс физики. М.: Высшая школа, 1990.

9.3 Детлаф А.А., Яворский Б.М. Курс физики. М.: Высшая школа, 1989.

9.4 Кортнев А.В. Практикум по физике. М.: Высшая школа, 1965.

Лабораторна робота №2 Дослідження електричного поля точкових зарядів

1 Мета роботи

Дослідити та провести комп'ютерне моделювання електричного поля точкових зарядів, підтвердження закономірності для цих полів, визначити величину електричної постійної.

2 Теоретичні відомості

У даній роботі використовуються комп'ютерні моделі, засновані на законі Кулона і на формулах обчислення силової й електричної характеристик електричного поля точкового заряду.

Фізичну величину, що визначає здатність тіл до електромагнітних взаємодій, називають електричним зарядом. Для дослідження та опису взаємодії електричних зарядів вводиться поняття точкового заряду, що, як і поняття матеріальної точки, є фізичною абстракцією. Точковий заряд – заряд, розподілений на тілі, лінійні розміри якого порівняно малі в порівнянні з відстанню до інших заряджених тіл, з якими він взаємодіє.

Взаємодію двох точкових електричних зарядів встановлює закон Кулона: сила взаємодії двох нерухомих точкових електричних зарядів прямо пропорційна добутку модулів цих зарядів і обернено пропорційна квадрату відстані між ними.

(1)

де F — сила взаємодії крапкових зарядів,

q₁ і q₂ - модулі зарядів,

ε — відносна діелектрична проникність середовища, у якому поміщені заряди (для повітря ε = 1),

г — відстань між ними,

k — коефіцієнт пропорційності.

Величина коефіцієнта пропорційності k залежить від вибору системи одиниць: у СГС k=1, у СІ k = 9×10⁹ Н×м²/Кл² - це значення виходить при підстановці в формулу (2) чисельного значення величини , що називається електричної постійної, рівного

. (2)

Вектор сили у законі Кулона, часто називають кулонівською силою, спрямований вздовж прямій, що з'єднуючі заряди. Сила Кулона є центральною силою відштовхування (F>0) при однакових знаках зарядів (при однойменних зарядах) і силою притягання (F<0) при різних знаках зарядів. Кулонівські сили підпорядковуються третьому закону Ньютона, оскільки вони рівні за модулем; спрямовані протилежно одна одній уздовж прямої, що з'єднує точкові заряди; діють парами; є силами однієї природи; прикладені до різних тіл.

Переносником взаємодії електричних зарядів є електричне поле. Електричне поле — це форма матерії, що оточує електрично заряджені тіла. Електричне поле, що оточує нерухомі заряди - джерела поля, називається електростатичним (тобто полем нерухомих зарядів).

Силовою характеристикою електростатичного поля в даній точці є векторна величина, названа напруженістю електростатичного поля.

Напруженість електростатичного поля — фізична величина, обумовлена силою, що діє на одиничний позитивний точковий (пробний) заряд, поміщений у дану точку поля:

(3)

Вектор напруженості співнапрямлений з вектором сили, що діє на позитивний пробний заряд, внесений у дану точку електричного поля.

Напрямок і величина вектора напруженості електричного поля в даній точці визначаються винятково знаком заряду-джерела. Вектор напруженості електричного поля в даній точці має свій напрямок і величину, навіть якщо в цієї точці ніякого пробного заряду немає: якщо поле створюється позитивним зарядом, то вектор E спрямований уздовж радіуса-вектора від заряду в зовнішній простір (відштовхування пробного позитивного заряду), якщо поле створюється відємним зарядом, то вектор E спрямований до заряду.

Напруженість поля точкового заряду у вакуумі обчислюється по формулі

(4)

відповідно до якої напруженість електричного поля крапкового заряду-джерела Q у деякій точці поля прямо пропорційна величині цього заряду і обернено пропорційна квадрату відстані r між цією точкою поля і зарядом-джерелом.

Сила, що діє на будь-який заряд q, розміщений у дану точку поля, з сторони електричного поля, обчислюється по формулі

(5)

де - вектор напруженості в тій точці електричного поля, у яку поміщено заряд q. Тому що заряд q – це скалярна постійна величина, то напрямок вектора сили визначається напрямком вектора напруженості електричного поля і залежить від знака заряду.

Енергетичною характеристикою електростатичного поля в даній точці є скалярна величина, називана потенціалом електростатичного поля.

Потенціал електростатичного поля — фізична величина, чисельно рівна потенційної енергії, якою володівби в даній точці поля одиничний позитивний (пробний) заряд

. (6)

Потенціал поля точкового заряду у вакуумі обчислюється по формулі

(7)

відповідно до якої потенціал електричного поля точкового заряду-джерела Q у деякій точці поля прямо пропорційний величині цього заряду й оберненопропорційний відстані r між цією точкою поля й зарядом-джерелом.

Відкрийте комп'ютерну модель «Електричне поле точкових зарядів».

Уважно розгляньте модель, знайдіть всі регулятори й інші основні елементи й замалюйте їх у звіт. Модель має дві конфігурації - "Один заряд" і "Два заряди" і дві мітки - "Силові лінії" і "Еквіпотенціали". У цієї моделі при конфігурації "Два заряди" можна змінювати за допомогою движків величину зарядів і відстань між зарядами. Чисельні значення напруженості Е і потенціалу φ з'являються у вікні моделі при дослідженні електричного поля. Для цього необхідно встановити курсор (тут він має вигляд руки) у точку поля, натиснути ліву кнопку миші й при натиснутій кнопці миші на екрані фіксуються чисельні значення напруженості Е и потенціалу φ у досліджуваній точці електричного поля.

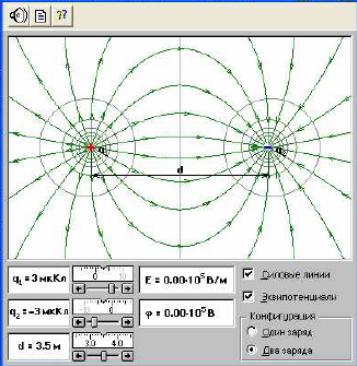
Рис. 1. Вікно комп'ютерної моделі «Електричне поле точкових зарядів» при конфігурації "Два заряди".

Відкрийте комп'ютерну модель «Взаємодія електричних зарядів».

Уважно розгляньте модель, знайдіть всі регулятори й інші основні елементи й замалюйте їх у звіт. У цій моделі можна не тільки змінювати за допомогою движків величину зарядів (величина яких виводиться в лівому нижньому куті вікна моделі), але й міняти відстань між зарядами за допомогою мишки, "зачепивши" заряд і переміщаючи його на необхідну відстань (воно фіксується як відстань між зарядами r_ij). При зміні величини зарядів і відстані між ними змінюється значення кулонівськой сили взаємодії між зарядами F_ij, напрямок якої зображено у вигляді стрілочок.

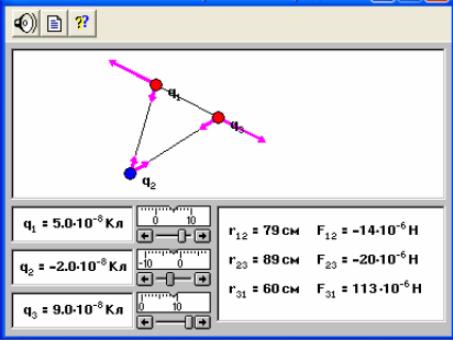
Рис. 2. Вікно комп'ютерної моделі «Взаємодія крапкових зарядів».

При використанні цієї комп'ютерної моделі у віртуальному експерименті 3, встановлюють значення заряду q₃ = 0 Кл, а для заряду q₂ мінімальне. Таким чином, цю модель можна використовувати для дослідження величини силової характеристики (напруженості Е) електричного поля точкового заряду-джерела q₁. Величину напруженості електричного поля в досліджуваній точці можна розрахувати по формулі

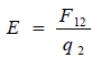, (8)

де F₁₂ - величина сили взаємодії між зарядами q₁ і q₂.