8 Питання вихідного контролю:

8.1 Запишіть умову яка визначає резонансну частоту і амплітуду при резонансі.

2. Що таке добротність, від чого залежить ця величина, наведіть необхідну формулу.

3. Вимушені коливання. Струм і напруга при послідовному резонансі.

4. Будова і робота найпростішого лампового генератора електричних коливань.

9. Перелік посилань

1. Лабораторний практикум з фізики. Навч.посібник/за ред. І.Є.Лопатинського, Львів: вид.НУ «Львівська політехніка»2002. ч.1. ст.54-60.

2. Загальна фізика: Лабораторний практикум.: Навч.посібник / В.М. Барановський, П.В.Бережний, І.Т.Горбачук та ін.; За заг.ред. І.Т.Горбачука. – К.: Вища шк.., 1992-509 с.

Лабораторна робота №13 Дослідження фігур Ліссажу

1 Мета роботи

Вивчення додавання двох взаємно перпендикулярних гармонійних коливань

2 Теоретичні відомості

1 Припустимо, що є дві взаємно перпендикулярні векторні величини і , що змінюються з часом з однаковою частотою ω за гармонічним законом

(1)

Тут – орти координатних осей X і Y , A і B – амплітуди коливань. Величинами і можуть бути, наприклад, зміщення матеріальної точки від положення рівноваги або напруженості двох взаємно перпендикулярних електричних полів і т.п.

У випадку частинки, яка коливається, величини

(2)

визначають координати частинки на площині XY . У випадку електричних полів величини (2) визначають координати кінця результуючого вектора напруженості поля .

Частинка або кінець вектора будуть рухатися по деякій траєкторії, вид якої залежить від різниці фаз обох коливань α. Вирази (2) фактично задають у параметричній формі рівняння цієї траєкторії. Щоб отримати рівняння траєкторії у звичайному вигляді, потрібно виключити з рівнянь (2) параметр t. З першого рівняння випливає, що

(3)

Звідси

(4)

Розкладемо косинус у другому рівнянні (2) за формулою для косинуса суми:

,

підставляючи при цьому замість cosωt і sinωt їх значення (3) і (4). У результаті отримаємо

Це рівняння за допомогою простих перетворень можна звести до вигляду

(5)

Ми отримали рівняння еліпса, осі якого повернуті відносно координатних осей X і Y .

Орієнтація еліпса і його півосі залежать від амплітуд A і B й різниці фаз α.

2 Проведемо дослідження отриманого результату (5). Визначимо форму траєкторії для ряду окремих випадків.

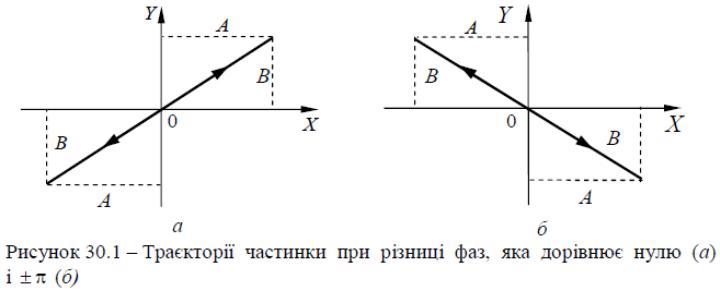
1 Різниця фаз α дорівнює нулю. У цьому випадку рівняння (5) спрощується таким чином:

Звідси отримуємо рівняння прямої:

(6)

Результуючий рух є гармонічним коливанням уздовж цієї прямої із частотою ω й амплітудою, яка дорівнює (рис. 30.1а).

2 Різниця фаз α дорівнює ± π. Рівняння (5) набуває вигляду

Отже, результуючий рух є гармонічним коливанням уздовж прямої

(7)

3 При α = ±π/2 рівняння (5) переходить у рівняння еліпса, приведеного до координатних осей:

(8)

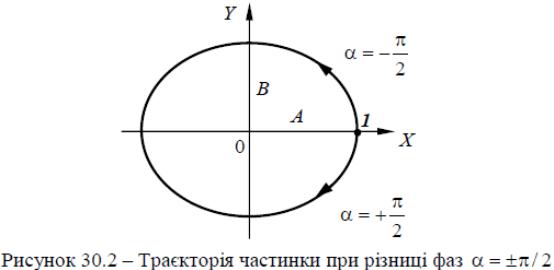
Півосі еліпса дорівнюють відповідним амплітудам коливань. При рівності амплітуд A і B еліпс перетворюється у коло.

Випадки α= +π/2 і α= -π/2 відрізняються напрямом руху по еліпсу або колу. Якщо α= +π/2, рівняння (2) можна записати таким чином:

(9)

У момент t = 0 тіло знаходиться у точці 1 (рис. 30.2). У наступні моменти часу координата x зменшується, а координата y стає від’ємною. Отже, рух відбувається за годинниковою стрілкою.

При α= -π/2 рівняння (2) мають вигляд

.

Звідси робимо висновок, що рух відбувається проти годинникової стрілки. Зі сказаного випливає, що рівномірний рух по колу радіуса R з кутовою швидкістю ω може бути поданий як сума двох взаємно перпендикулярних коливань:

(10)

(знак плюс у виразі для y відповідає руху проти годинникової стрілки, знак мінус – руху за годинниковою стрілкою).

3 У випадку, коли частоти взаємно перпендикулярних коливань відрізняються на

дуже малу величину Δω, їх можна розглядати як коливання однакової частоти, але з повільно змінною різницею фаз. Дійсно, рівняння коливань можна подати у вигляді

і вираз Δωt +α розглядати як різницю фаз, що повільно змінюється з часом за лінійним законом. Результуючий рух у цьому випадку відбувається по повільно змінній кривій, яка буде послідовно набирати форми, що відповідає всім значенням різниці фаз від -π до +π .

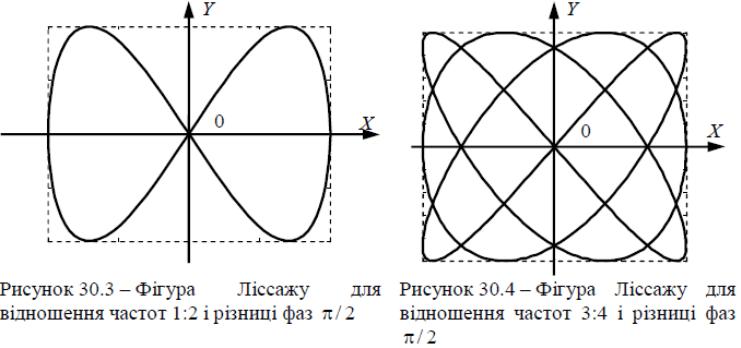
4 Якщо частоти взаємно перпендикулярних коливань не однакові, то траєкторії результуючого руху мають вигляд досить складних кривих, які називаються фігурами Ліссажу. На рис. 30.3 і рис. 30.4 наведені приклади таких фігур. Іноді фігурами Ліссажу називають також і траєкторії (зокрема, еліптичні криві), які виникають при складанні взаємно перпендикулярних коливань однакової частоти.

Для знаходження аналітичного виду рівняння кривих – фігур Лиссажу – треба з рівнянь коливань (1) виключити час t. Однак у загальному випадку ця процедура складна навіть при рівності частот, і тому одержувати рівняння фігур Ліссажу не будемо.

На рис.30.5 зображена одна з найпростіших фігур Ліссажу, що виходить при додаванні взаємо-перпендикулярних коливань, причому частота коливання по осі Y в 2 рази більше, ніж по осі Х. Малюнок пояснює правило частот Ліссажу, відповідно до якого можна визначити відношення частот коливань, що складаються. Про величину цього відношення судять по відношенню чисел точок перетину фігури із двома намальованими для цієї мети прямими лініями, паралельними осям координат і які не проходять через центр і точки с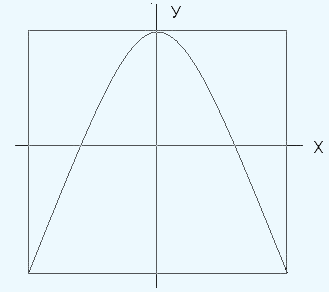 амоперетинання фігури. На рис. 30.5 видно, що частоти коливань, що складаються, співвідносяться як . При цьому частота коливання менше в тому напрямку, у якому є більше точок перетину. Так, судячи з мал. 30.5, частота коливань у напрямку горизонтальної осі в 2 рази менше, ніж у напрямку вертикальної осі

3 Підготовка до роботи

3.1 Ознайомитись з інструкцією.

3.2 Опрацювати теоретичний матеріал за темою роботи

3.3 Письмово відповісти на питання вихідного контролю.

3.4 Продумати методику виконання роботи.

3.5 Ознайомитись з правилами оформлення звітів і підготувати бланк звіту по даній роботі

4 Інструменти, обладнання і прилади

Комп’ютер, програмне забезпечення, калькулятор, лінійка, олівець, міліметровий папір.