8 Питання вихідного контролю:

8.1 Під дією яких сил здійснюються гармонічні коливання?

8.2 Що таке період коливання?

8.3 Чому для визначення прискорення вільного падіння вимірюють періоди і різницю довжин двох математичних маятників, а не користуються одним математичним маятником, обчислюючи g із формули (5) ?

4. В якій точці траєкторії кулька математичного маятника досягає найбільшого прискорення?

9 Перелік посилань

9.1 Лабораторний практикум з фізики. Навч.посібник/за ред. І.Є.Лопатинського, Львів: вид.НУ «Львівська політехніка»2002. ч.1. ст.54-60.

9.2 Загальна фізика: Лабораторний практикум.: Навч.посібник/ В.М.Барановський, П.В.Бережний, І.Т.Горбачук та ін.; За заг.ред. І.Т.Горбачука. – К.: Вища шк.., 1992-509 с.

Лабораторна робота №11 Вивчення законів коливального руху за допомогою фізичного маятника

1 Мета роботи

Визначити прискорення сили ваги шляхом вивчення руху фізичного маятника.

2 Теоретичні відомості

Гармонічним (квазіпружним) коливанням фізичної величини х називається процес зміни її з часом t по закону синуса або косинуса:

х = Аsin(ω t + φ₀), (1)

або при φ_{0 =} х =Acosωt

Рівняннями (1) задаються основні характеристики гармонічних коливань:

а) х – зміщення коливальної системи від положення рівноваги в довільний момент часу;

б) А – амплітуда – найбільше зміщення коливальної системи від положення рівноваги;

в) φ=ωt + φ₀ - фаза коливання; φ_о - початкова фаза;

г) ω= - колова (циклічна) частота;

д) Т - період коливання – найменший проміжок часу, після проходження якого рух знову точно повторюється;

е) = - частота коливань – кількість коливань N за одиницю часу t.

Гармонічні коливання здійснюються під дією пружних сил типу Гука

F= - kx, (2)

тому їх називають також квазіупружними, k – коефіцієнт пружності.

Гармонічні коливання є незгасаючими коливаннями, динамічна модель яких задається диференціальним рівнянням (3), розв’язками якого є рівняння (1).

х" + ω х = 0 (3)

де ω_o - власна частота коливальної системи.

За допомогою рівняння (3) можна оцінити, в першому наближенні, власні частоти і, відповідно, періоди коливань простих коливальних систем, наприклад: пружинного, математичного, фізичного, крутильного маятників, електромагнітного коливального контура та інших.

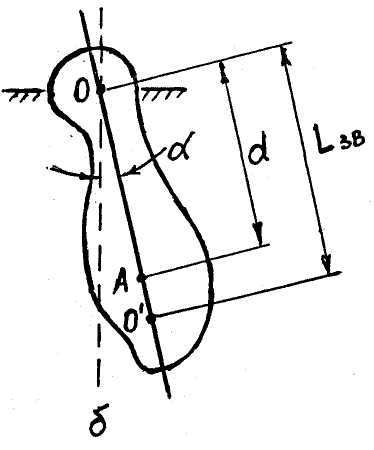
Фізичним маятником називається тверде тіло довільної форми, яке під дією сили тяжіння здійснює коливання навколо нерухомої горизонтальної осі О, що не проходить через його центр ваги (Мал.1б).

, (4)

де I – момент інерції тіла відносно осі обертання;

m – маса маятника;

g – прискорення сили тяжіння;

x – відстань від осі обертання до центра маси тіла. Формулу (8.3) можна представити у вигляді

, (5)

де величина називається зведеною довжиною фізичного маятника.

Математичний маятник довжиною l=l_зв коливається з таким періодом коливань, що й фізичний маятник.

Зведена довжина фізичного маятника L_зв, – це довжина такого математичного маятника, період коливань якого збігається з періодом коливань даного фізичного маятника.

Оборотний маятник – це фізичний маятник, що має дві осі обертання О та О', паралельні одна одній. Ці осі знаходяться на віддалі L_зв,.

Точка підвісу О і центр гойдання О', мають властивість взаємозамінності: при перенесенні точки підвісу у центр гойдання О', попередня точка підвісу О стає новим центром гойдання. Період коливань при цьому не змінюється.

Математичний маятник можна розглядати як частковий випадок фізичного маятника, вся маса якого зосереджена в одній точці - центрі ваги.

Мал.1.Схематичне зображення фізичного маятника

О – точка підвісу; - кут відхилення від положення рівноваги; ℓ - довжина маятника. А – центр ваги; О' – центр гойдання; Lзв – зведена довжина; d – відстань між точкою підвісу і центром ваги.