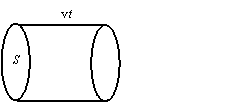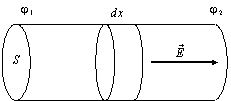8 Питання вихідного контролю:

8.1 У яких одиницях вимірюється напруга, ЕРС, потенціал, сила струму, опір, провідність.

8.2 Скільки міліамперів у 1 Ампері?

9 Перелік посилань

9.1 Лабораторний практикум з фізики. Навч.посібник/за ред. І.Є.Лопатинського, Львів: вид.НУ «Львівська політехніка»2002. ч.1. ст.54-60.

9.2 Загальна фізика: Лабораторний практикум.: Навч.посібник/ В.М.Барановський, П.В.Бережний, І.Т.Горбачук та ін.; За заг.ред. І.Т.Горбачука. – К.: Вища шк.., 1992-509 с.

Лабораторна робота №6 Вивчення закону Ома

1 Мета роботи

Вивчення руху зарядів в середині провідника і перевірка закону Ома для провідників.

2 Теоретичні відомості

Елементарна теорія закону Ома

Електропровідність провідника визначається наявністю в ньому вільних носіїв заряду (електрони в металі, позитивні і негативні іони в електролітах). Припустимо, що носії струму слабко взаємодіють один з одним, а взаємодія їх з іншими частками зводиться до зіткнень. Крім того, будемо вважати, що рух цих часток описується законам класичної механіки, що справедливо для напівпровідників або електролітів, але не справедливо для металів.

Під час відсутності електричного поля частки в провіднику (які приблизно можна вважати вільними) здійснюють хаотичний рух, зіштовхуючись при цьому з іонами на вузлах кристалічної гратки, з атомами домішок і т.д. Всі напрямки руху вільних часток рівноправні, і якого-небудь потоку часток, тобто струму, не виникає. Тому усереднені по всьому об’ємі, проекції швидкості дорівнюють нулю. Якщо провідник перебуває в електричному полі, то на частки діють спрямовані сили. Якщо стежити за якою-небудь часткою, то можна виявити, що на тепловий хаотичний рух частки накладається її спрямований рух під дією сили з боку електричного поля (так званий дрейф).

Розглянемо рух однієї частки. Нехай заряджена частка із зарядом е й масою m рухається в однорідному електричному полі. Сила, що діє на частку з боку поля, дорівнює , де  – напруженість поля, яку можна вважати постійною. Тоді рівняння її руху має вигляд:

.

Нехай вектор напруженості спрямований по осі Ох, тоді прискорення частки теж спрямовано по цій осі й дорівнює . Якщо початкова швидкість частки дорівнює нулю, то в момент часу t вона дорівнює , а середня швидкість удвічі менше, за деякий проміжок часу τ вона дорівнює

(1)

Приймемо таку модель. Будемо вважати, що заряджені частки, що рухаються, зіштовхуються з іншими частками через однаковий час, який можна ототожнити із середнім часом між зіткненнями. Будемо вважати, що в середньому в результаті зіткнення частки зупиняються, а після цього вони знову починають рух в електричному полі з нульовою початковою швидкістю. Із цієї причини можна вважати, що частки рухаються в електричному полі із середньою швидкістю, що визначається з формули (1). 

Рис. 1

Сила струму – це заряд, який переноситься частками, що рухаються, за одиницю часу, а густина струму дорівнює силі струму через переріз провідника із площею, яка рівна одиниці. Знайдемо зв'язок між густиною струму і швидкістю спрямованого руху часток. Нехай частки рухаються вліво зі швидкістю v (рис. 1). За час t вони проходять шлях, рівний l = vt. Таким чином, за цей час переріз S провідника перетнуть тільки ті частки, які знаходяться від нього на відстані, меншій або рівній l, тобто ті частки, які перебувають всередині циліндра висотою l = vt і об'ємом V = S(vt). Якщо концентрація часток дорівнює n, то їхнє число в цьому об'ємі дорівнює N = nV = nS(vt). Нехай заряд однієї частки дорівнює q. Тоді за час t через переріз провідника протікає сумарний заряд N часток, рівний Q = q = qnSvt. Отже, сила струму через провідник дорівнює , а густина струму – .

В розглянутому нами випадку вектор густини струму  спрямований у напрямку прикладеного поля, тобто уздовж осі Ох. Величина j пропорційна середній швидкості спрямованого руху, а саме j = еnavn. Підставляючи сюди avn з формули (1), одержимо:

(2)

Це вираз називають законом Ома в диференціальній формі. Величина

(3)

називається коефіцієнтом електропровідності або просто електропровідністю даного провідника, а коефіцієнт пропорційності між середньою швидкістю спрямованого руху зарядів avn і напруженістю прикладеного електричного поля Е називають рухливістю носіїв струму. З формули (2) видно, що рухливість виражається в такий спосіб:

.

Електропровідність і рухливість зв'язані один з одним співвідношенням: s = enl.

Зміст закону Ома полягає в тому, що середня швидкість спрямованого руху носіїв струму пропорційна напруженості електричного поля, тобто пропорційна діючої на частки силі. Закон Ома виконується для металів, напівпровідників, електролітів, тобто для тих речовин, у яких носії струму зазнають велику кількість зіткнень. При цьому даний закон виконується при не занадто сильних полях, коли роль зіткнень велика. Закон Ома не виконується при струмах у вакуумі, тому що в цьому випадку носії струму практично не зазнають зіткнень. Закон Ома дуже обмежено виконується в плазмі, тому що в плазмі звичайно непостійне число носіїв струму. Відзначимо, що вираз для коефіцієнта електропровідності (3) відповідає дослідним даним набагато гірше, ніж сам закон Ома. Цей вираз більш-менш можна застосувати для напівпровідників або електролітів, але зовсім не придатний для металів, у той час як сам закон Ома для металів виконується досить добре.

Звичайно у фізиці і особливо в електротехніці застосовується закон Ома в іншому виді - у так називаній інтегральній формі. Одержимо вид цього закону.

Рис. 2

Розглянемо ділянку однорідного провідника, що має для простоти циліндричну форму (рис. 2). Нехай площа поперечного перерізу провідника S, а довжина l. До кінців провідника прикладена різниця потенціалів U = φ₁ – φ₂, тобто усередині провідника діє електричне поле . Тому в провіднику виникає електричний струм, густина струму, відповідно до закону Ома, j = sЕ. Якщо струм розподілений рівномірно по перетині провідника, то сила струму I = j = sES.

У випадку однорідного поля напруженість поля Е пов'язана з потенціалом співвідношенням: . Тому сила струму в провіднику , звідки .

Величина  (питомий опір ) називається опором даної ділянки провідника. Тоді закон Ома в інтегральній формі має вигляд:

IR = φ₁ – φ₂ = U. (5)

3 Підготовка до роботи

3.1 Ознайомитись з інструкцією.

3.2 Опрацювати теоретичний матеріал за темою роботи

3.3 Письмово відповісти на питання вихідного контролю.

3.4 Продумати методику виконання роботи.

3.5 Ознайомитись з правилами оформлення звітів і підготувати бланк звіту по даній роботі

4 Інструменти, обладнання і прилади

Комп’ютер, програмне забезпечення, калькулятор, лінійка, олівець, міліметровий папір.