1.3 Определите значимость переменных:

Значимость коэффициентов уравнения регрессии а₀, а₁, а₂ оценим с использованием t-критерия Стьюдента.

- коэффициент свободного члена незначим

- коэффициент перед х₁ значим

Расчетные значения t-критерия Стьюдента для коэффициентов уравнения регрессии, приведены в столбце “t-статистика” таблицы 3.

Табличное значение t-критерия при 5% уровне значимости и степенях свободы (30 – 1 – 1 = 28) составляет 2,368, если |t_расч| > t_табл, то коэффициент - существен (значим).

1.4 Найдем среднюю ошибку аппроксимации:

.

А = 752,84/30 = 25,09%

В среднем расчетные значения для линейной модели отличаются от фактических значений на 25,09%. Модель не достаточно точная.

д) Вычислим коэффициент детерминации:

R² = 0,557

Вариация результата Y на 55,7% объясняется вариацией фактора X₁.

1.5 линейные коэффициенты корреляции между всеми членами регрессии:

- линейный коэффициент корреляции между х₁ и y

Связь между фактором y и х₁ заметная, прямая.

1.6 Проверим гипотезу о значимости уравнения с помощью критерия Фишера:

Сравним F_факт с F_табл при уровне значимости α=0,05 и количестве степеней свободы k₁ = m = 1, k₂ = n - m – 1 = 30 – 1 – 1 = 28.

F_табл(1; 28) = 4,196.

Так как F_факт > F_табл, то уравнение регрессии в целом значимо.

1.7 Проверим модель на отсутствие автокорреляции.

Так как

, то уровни ряда остатков независимы.

Воспользуемся критерием по первому коэффициенту автокорреляции:

то гипотеза об отсутствии автокорреляции в ряду остатков может быть принята, следовательно, свойство выполняется.

1.8 Проверка на гетероскедастичность моделей

1. Нормальное распределение случайных возмущений для всех наблюдений.

2. Средние значения случайных возмущений в каждом наблюдении равно нулю.

3. Распределения одинаковы для всех наблюдений.

Так как все условия выполняются, то гипотеза о гомоскедастичности случайных возмущений принимается.

Поле корреляции между независимой переменной и квадратом случайной ошибки выглядит следующим образом (рис. 2)

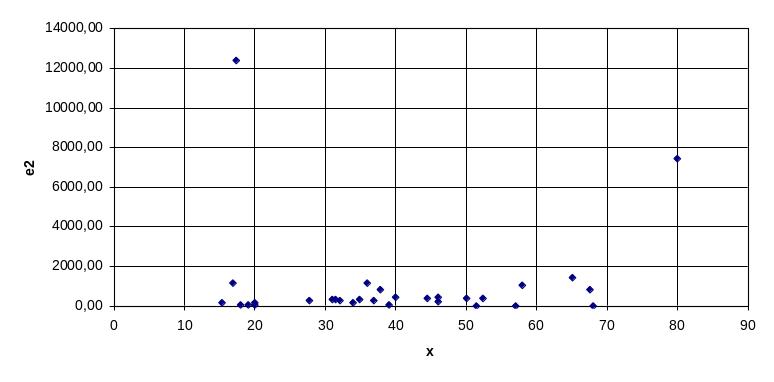
Рис. 2 - Графический анализ остатков

Таким образом, полученные оценки коэффициентов регрессионного уравнения действительно являются несмещенными, эффективными и состоятельными, а само уравнение может использоваться для моделирования и прогнозирования стоимости квартиры.

2. Построим линейную множественную регрессию.

2.1 Оценим параметры уравнения с помощью метода наименьших квадратов.

Составим систему уравнений:

Найдем коэффициенты уравнения в программе Excel. Сервис – Анализ данных – Регрессия.

Таблица 6 - Результат регрессионного анализа

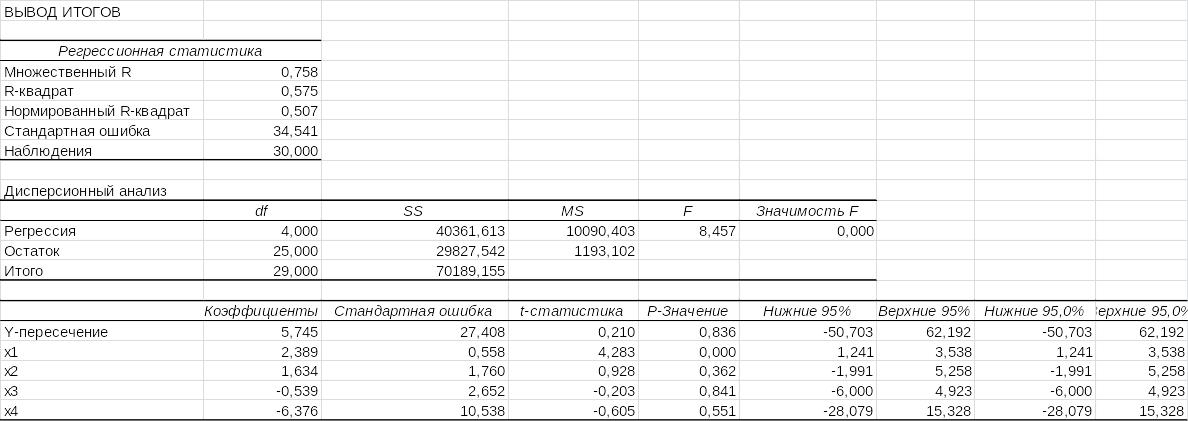
Таким образом, теоретическое уравнение множественной регрессии имеет вид:

Коэффициенты регрессии приведены в столбце“Коэффициенты”таблицы 6.

2.2 Оценим адекватность построенной модели по критерию:

• случайности остаточной компоненты по критерию пиков.

Таблица 7 - Расчет адекватности модели

t	E(t)	E2(t)	E(t)-E(t-1)	[E(t)-E(t-1)]2	E(t)*E(t-1)	|E(t)/Y(t)|*100 %
1	5,366	28,797	-	-	-	4,67
2	20,688	427,992	15,322	234,753	111,018	24,34
3	16,024	256,759	-4,664	21,755	331,498	23,22
4	13,226	174,931	-2,798	7,826	211,932	23,20
5	-39,508	1560,877	-52,734	2780,886	-522,539	21,40
6	-14,364	206,337	25,144	632,196	567,509	25,65
7	16,313	266,114	30,677	941,104	-234,327	19,19
8	-86,156	7422,888	-102,469	10499,931	-1405,465	32,51
9	21,363	456,388	107,519	11560,427	-1840,575	35,22
10	-0,615	0,378	-21,978	483,030	-13,132	0,47
11	-7,339	53,856	-6,724	45,212	4,511	15,95
12	-26,933	725,390	-19,594	383,940	197,654	23,42
13	11,907	141,772	38,840	1508,537	-320,687	16,84
14	6,790	46,110	-5,116	26,177	80,853	17,19
15	-23,607	557,291	-30,397	924,006	-160,303	29,92
16	27,335	747,209	50,942	2595,100	-645,300	45,56
17	21,990	483,571	-5,345	28,568	601,106	21,99
18	31,349	982,781	9,359	87,592	689,380	61,47
19	-10,559	111,498	-41,909	1756,329	-331,026	6,73
20	37,382	1397,379	47,941	2298,319	-394,721	30,27
21	-11,036	121,793	-48,418	2344,257	-412,543	19,99
22	20,032	401,293	31,068	965,239	-221,076	20,98
23	14,161	200,542	-5,871	34,469	283,683	24,59
24	31,914	1018,476	17,752	315,143	451,937	49,48
25	15,733	247,517	-16,181	261,821	502,086	17,10
26	23,992	575,599	8,259	68,211	377,453	23,99
27	13,194	174,070	-10,798	116,599	316,535	25,87
28	-103,514	10715,102	-116,707	13620,600	-1365,714	65,93
29	-14,700	216,095	88,814	7887,857	1521,670	11,90
30	-10,428	108,736	4,272	18,254	153,289	18,89
Итого	0,000	29827,542		62448,138	-1465,294	757,95

Так как количество поворотных точек равно 20 (р = 20), то неравенство выполняется

p > 14; 20 > 14

Следовательно, свойство случайности выполняется.

• независимости уровней ряда остатков по d-критерию (d₁ = 1,08, d₂ = 1,36) или по первому коэффициенту корреляции, критический уровень которого равен r(1) = 0,36.

Так как

, то уровни ряда остатков независимы.

Воспользуемся критерием по первому коэффициенту автокорреляции:

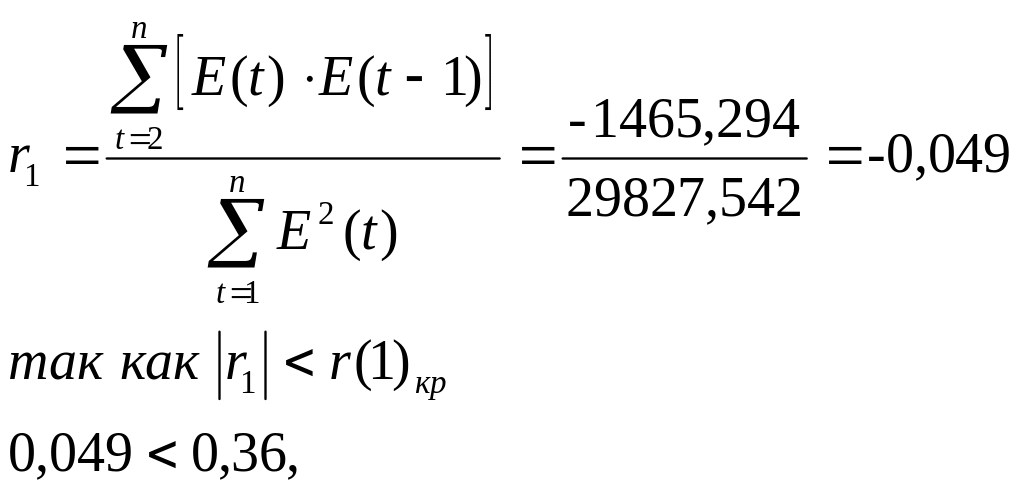
то гипотеза об отсутствии автокорреляции в ряду остатков может быть принята, следовательно, свойство выполняется.

• Нормальности распределения относительной компоненты по R/S – критерию с критическими уровнями 2,7 – 4,8

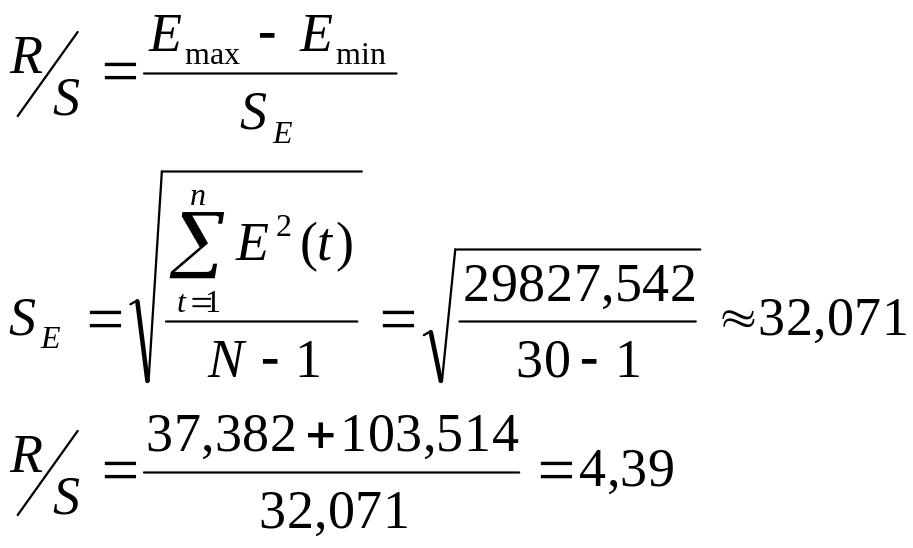
Так как расчетное значение попадает в интервал, следовательно, свойство нормальности распределения выполняется.

Так как выполняются все условия, то, следовательно, модель адекватна данному временному ряду.