Індивідуальна робота з теми «Вектори»
Дано точки А, В, С, D.
Знайдіть координати векторів
Знайдіть абсолютну величину векторів
Знайдіть скалярні добутки:
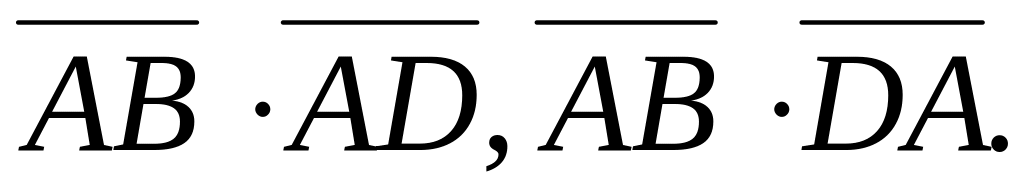
Визначите вид кута між векторами
й
і вид кута, утвореного векторами
й
.Знайдіть значення косинуса кута між векторами й і векторами и.
Знайдіть координати точок Р и К, якщо Р - середина відрізка ВР, а К - середина відрізка DС.
Знайдіть довжину відрізка РК.
Знайдіть координати векторів
й
.З'ясувати, чи будуть вектори й
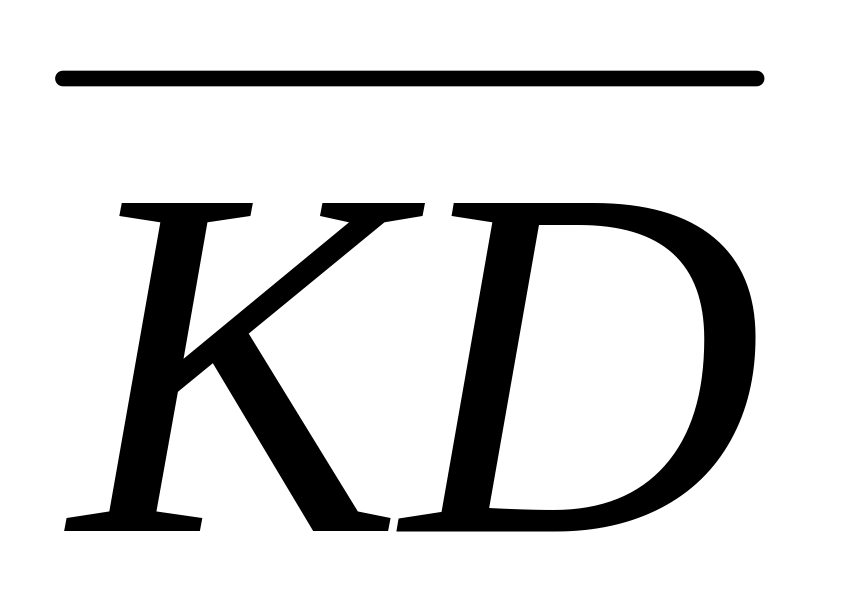перпендикулярними ?Встановити, чи є вектори й колінеарними ?
Встановити вид чотирикутника АВСD.
Встановити вид трикутника РСК.
Відкласти від точки D вектор, який дорівнює вектору
.Відкласти від початку координат вектор
,
заданий формулою
( двома способами ).Відкласти від початку координат вектор
,
заданий формулою
( двома способами ).Виразити вектор
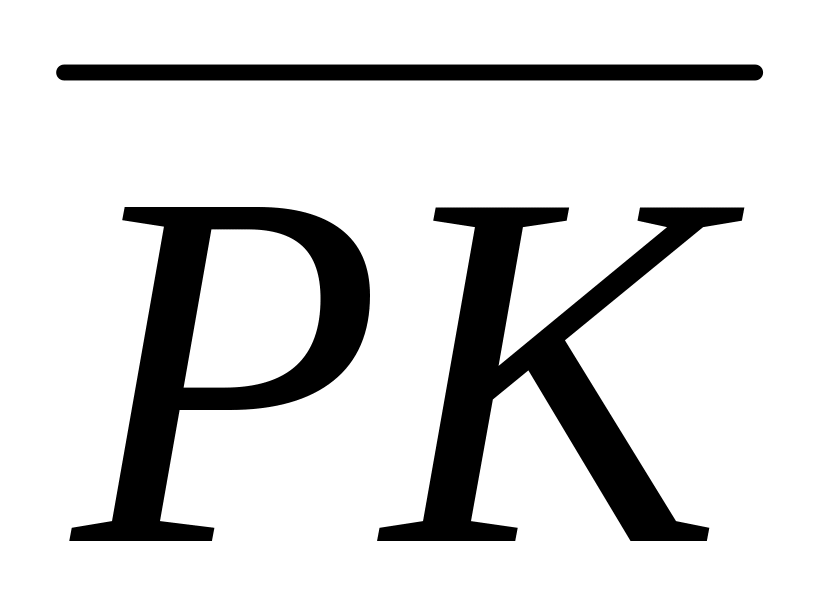через вектори
й
,
де Р и К - середини сторін ВР і DС
відповідно.Складіть рівняння окружності, діаметром якої є відрізок ВР.
Складіть рівняння прямої РК.
Варіанти завдань
1.А(-3; 5) В(- 3; 8) С( 2;10) D( 2; 7) |
14.А(2;3) В(3;5) С(10;1) D(11;-2) |
27.А(-2;-2) В(-4;-6) С(4;-10) D(6;-6) |
2.А(- 9; 1) В(- 7; 5) С( -3;7) D( -5; 3) |
15.А(7;-1) В(4;-4) С(-2;-6) D(1;-3) |
28.А(-8;-2) В(-10;1) С(-4;5) D(1;4) |
3.А(0; 0) В(0; 2) С( 6;8) D( 10; 10) |
16.А(-7;-2) В(-1;-3) С(0;-10) D(-7;-9) |
29.А(-6;-1) В(0;1) С(6;1) D(0;-1) |
4.А(-2;1) В(-1;6) С(-6;7) D(-7;2) |
17.А(-9;4) В(-8;7) С(-5;9) D(0;10) |
30.А(0;0) В(4;-1) С(5;-5) D(1;-4) |
5.А(-2;-2) В(0;2) С(6;8) D(10;10) |
18.А(4;-1) В(7;-4) С(4;-7) D(1;-4) |
31.А(-7;4) В(-3;2) С(-1;-2) D(-3;-4) |
6.А(2;3) В(3;5) С(10;1) D(9;-1) |
19.А(9;-4) В(11;2) С(12;2) D(14;-4) |
32.А(-2;0) В(-1;4) С(3;3) D(2;-1) |
7.А(-3;1) В(-1;7) С(2;6) D(-1;-3) |
20.А(-8;-2) В(-10;1) С(-1;7) D(1;4) |
33.А(-3;-2) В(-4;4) С(4;-4) D(-2;-3) |
8.А(-14;-2) В(-11;2) С(-3;2) D(-6;-2) |
21.А(-4;-6) В(-2;-2) С(2;-4) D(4;-10) |
34.А(-2;-1) В(-2;-2) С(7;-2) D(7;-1) |
9.А(6;0) В(5;-5) С(0;-6) D(1;-1) |
22.А(0;6) В(5;4) С(7;0) D(2;2) |
35.А(-2;-1) В(-2;-2) С(7;-2) D(3;-1) |
10.А(-4;-10) В(0;-6) С(4;-6) D(2;-10) |
23.А(0;2) В(1;5) С(0;8) D(-1;5) |
36.А(0;-6) В(4;-4) С(4;-8) D(0;-10) |
11.А(-5;-1) В(-2;-3) С(-4;-6) D(-7;-4) |
24.А(0;2) В(0;6) С(3;9) D(6;8) |
37.А(7;0) В(10;2) С(13;0) D(10;-2) |
12.А(-4;-10) В(0;-6) С(4;-6) D(8;-10) |
25.А(3;0) В(1;3) С(7;2) D(6;-1) |
38.А(4;-4) В(5;0) С(8;0) D(13;-4) |
13.А(-3;1) В(-1;7) С(2;6) D(0;0) |
26.А(0;2) В(0;6) С(3;9) D(7;9) |
|
Математичний диктант №1 Варіант 1 1.Запишіть коротко «вектор а». 2. Зобразити вектор . 3.Запишіть позначення вектора з кінцем у точці Х та початком у точці У. 4.Зобразити два однаково спрямованих, але не рівних вектора. 5.Що можна сказати про напрямок двох рівних векторів ? 6.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
7.
Зобразити вектор
8.
Запишіть за допомогою позначень
«довжина вектора
9.Знайдіть довжину вектора, зображеного на рисунку:
3 см S 5 см
10.
Чи вірно твердження: «Якщо вектори
|
Математичний диктант №1 Варіант 2 1.Запишіть коротко «вектор в».
2.
Зобразити вектор
3.Запишіть позначення вектора з кінцем у точці Р та початком у точці А. 4.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
5.
Зобразити вектор
6.Що можна сказати про напрямок двох рівних векторів ? 7.Зобразити два однаково спрямованих, але не рівних вектора.
8.
Запишіть за допомогою позначень
«довжина вектора
9.Знайдіть довжину вектора, зображеного на малюнку:
К 2 см 6 см 10. Чи вірно твердження: «Якщо два вектори колінеарні, то вони однаково спрямовані»?
|
Математичний диктант №2 Варіант 1 1. Знайдіть координати вектора , де А(1;3), В(-2;0). 2. Знайдіть довжину вектора
3.
Знайдіть суму векторів
(-3;2)
і
4. Чи колінеарні вектори (-1;2) і (2;-4)?
5.
Знайдіть скалярний добуток векторів
6.
Знайдіть скалярний добуток векторів
й
7. Чи перпендикулярні вектори
(-2;3)
і
8. Знайдіть кут між векторами (1;1) і (1;0). 9. Знайдіть косинус кута між векторами (-3;1) і (3;-4).
10.
Вектор
|
Математичний диктант №2 Варіант 2 1. Знайдіть координати вектора , де А(2;4), В(-3;0). 2. Знайдіть довжину вектора (6;-8). 3. Знайдіть суму векторів (-2;3) і (-4;7). 4. Чи колінеарні вектори (-2;4) і (6;-5) ? 5. Знайдіть скалярний добуток векторів (3;4) і (-2;1).
6.
Знайдіть скалярний добуток векторів
й
,
якщо
7. Чи перпендикулярні вектори (-3;2) і (4;6) ? 8. Знайдіть кут між векторами (2;2) і (0;2). 9. Знайдіть косинус кута між векторами (-2;1) і (4;-3). 10. Вектор має координати (-4;-3), а точка F(1;3). Знайдіть координати точки К.
|
Варіант 3 1. Знайдіть координати вектора , де А(3;5), В(-3;2). 2. Знайдіть довжину вектора (2;-4). 3. Знайдіть суму векторів (-4;2) і (5;7). 4. Чи колінеарні вектори (8;-4) і (-2;-1)? 5.Знайдіть скалярний добуток векторів (4;2) і (-2;1). 6. Знайдіть скалярний добуток векторів й , якщо а кут між цими векторами дорівнює 1500. 7. Чи перпендикулярні вектори (3;2) і (-4;6) ? 8. Знайдіть кут між векторами (-1;1) і (-1;0). 9.Знайдіть косинус кута між векторами (3;1) і (3;4). 10. Вектор має координати (2;11), а точка F(2;-3). Знайдіть координати точки К. |
Варіант 4 1. Знайдіть координати вектора , де А(4;6), В(-2;4). 2. Знайдіть довжину вектора (-8;2). 3. Знайдіть суму векторів (2;-6) і (4;-8). 4. Чи колінеарні вектори (7;-3) і (1;-4)? 5.Знайдіть скалярний добуток векторів (3;2) і (-4;6). 6. Знайдіть скалярний добуток векторів й , якщо а кут між цими векторами дорівнює 1350. 7. Чи перпендикулярні вектори (4;2) і (-2;1) ? 8. Знайдіть кут між векторами (-2;2) і (0;-2). 9.Знайдіть косинус кута між векторами (2;1) і (4;3). 10. Вектор має координати (-9;10), а точки F(4;-3). Знайдіть координати точки К. |
і точку У. Відкладіть від точки У
вектор, рівний
.
дорівнює 3 см».
Т
й
рівні, то вони колінеарні»?
.
і точку М. Відкладіть від точки М
вектор, який дорівнює вектору
.
дорівнює 4 см».
М
(-3;4).
(-4;5).
(1;5) і
(-3;-2).
,
якщо
а кут між цими векторами дорівнює
300.
(-1;2)?
має координати (-3;8), а точка
F(5;2). Знайдіть координати точки К.
а кут між цими векторами дорівнює
450.