3. Плоскость в пространстве

Всякое уравнение первой степени относительно координат

(3.1)

задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости.

Вектор , ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0.

Особые случаи уравнения (3.1):

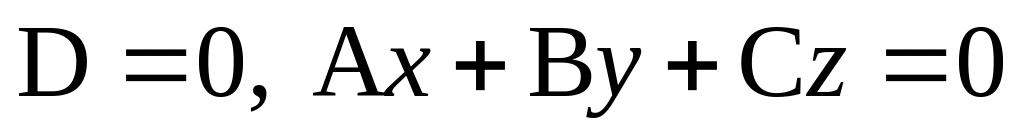1. ‑ плоскость проходит через начало координат.

2. ‑ плоскость параллельна оси Oz.

3. ‑ плоскость проходит через ось Oz.

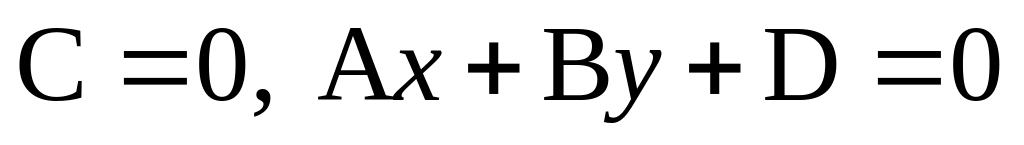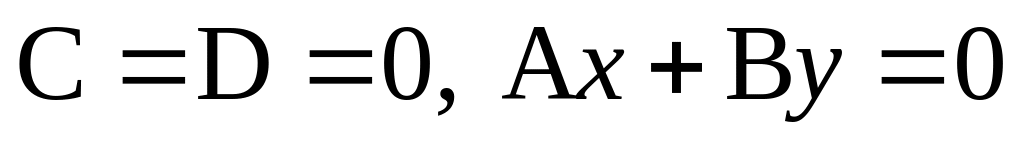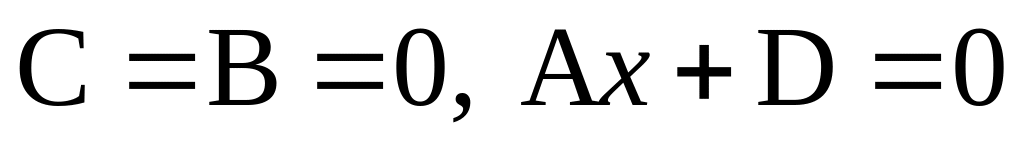4. ‑ плоскость параллельна плоскости Oyz.

Уравнения координатных плоскостей: .

Пример 1.15. Cоставьте уравнение плоскости, зная, что точка служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.

Решение. По условию задачи вектор является нормальным вектором плоскости, тогда ее уравнение можно записать в виде . Подставив координаты точки , принадлежащей плоскости, найдем D: . Итак, .

Пример 1.16. Составьте уравнение плоскости, проходящей через ось Оz и образующей с плоскостью угол 60^о.

Решение. Плоскость, проходящая через ось Oz, задается уравнением , где А и В одновременно не обращаются в нуль. Пусть В не равно 0, . По формуле косинуса угла между двумя плоскостями

, где .

Решая квадратное уравнение , находим его корни , , откуда получаем две плоскости и .

4.1.Матрицы. Операции над матрицами

Прямоугольной матрицей размера ( ) называется совокупность чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать матрицу в виде

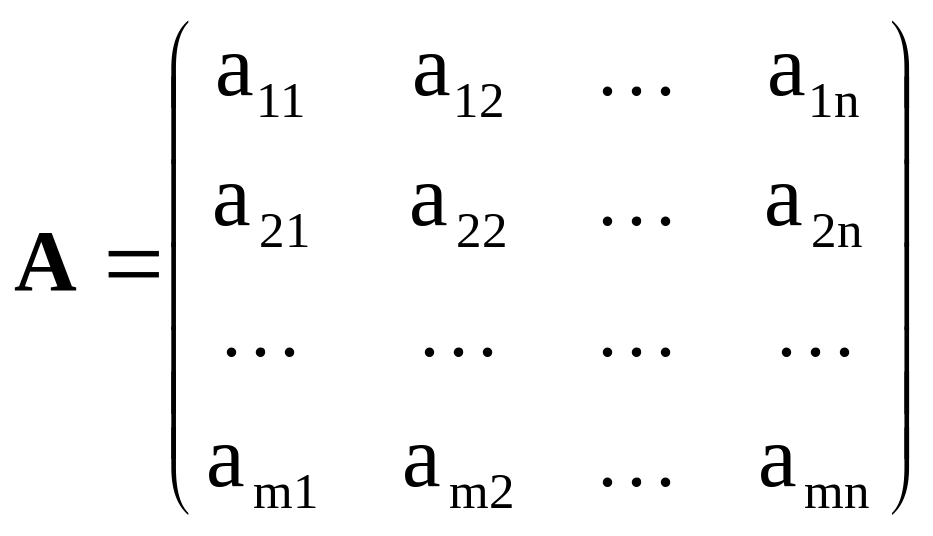(4.1)

или сокращенно в виде . Числа , составляющие данную матрицу, называются ее элементами; первый индекс указывает на номер строки, второй - на номер столбца. Две матрицы и одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть , если .

Матрица, состоящая из одной строки или одного столбца, называется соответственно вектор-строкой или вектор-столбцом. Вектор-столбцы и вектор-строки называют просто векторами.

Матрица, состоящая из одного числа, отождествляется с этим числом. Матрица размера , все элементы которой равны нулю, называются нулевой матрицей и обозначается через 0. Элементы матрицы с одинаковыми индексами называют элементами главной диагонали. Если число строк матрицы равно числу столбцов, то есть , то матрицу называют квадратной порядка . Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами и записываются так:

.

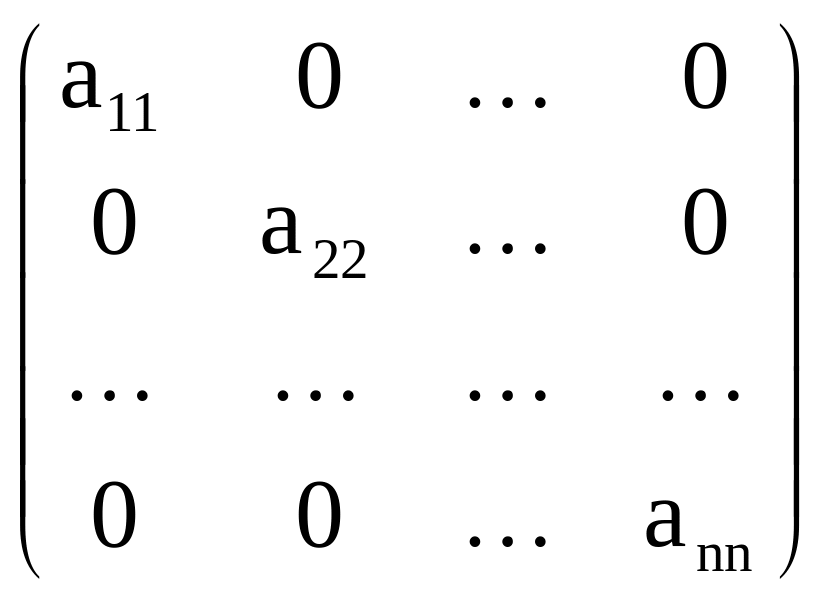Если все элементы диагональной матрицы равны 1, то матрица называется единичной и обозначается буквой :

.

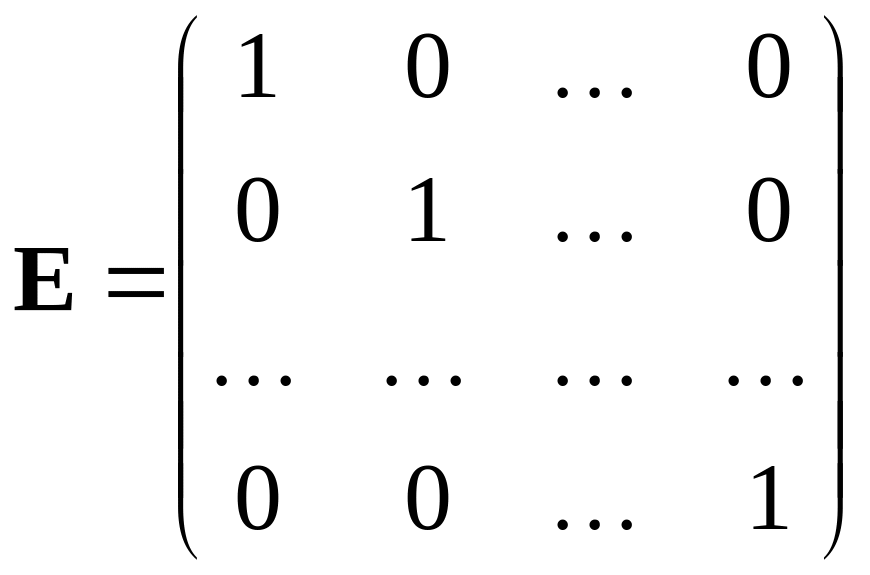Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю. Транспонированием называется такое преобразование матрицы, при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком наверху.

Пусть дана матрица (4.1). Переставим строки со столбцами. Получим матрицу

_,

которая будет транспонированной по отношению к матрице . В частности, при транспонировании вектора-столбца получается вектор-строка и наоборот.

Произведением матрицы на число l называется матрица, элементы которой получаются из соответствующих элементов матрицы умножением на число l: .

Суммой двух матриц и одного размера называется матрица того же размера, элементы которой определяются по формуле .

Произведение матрицы на матрицу определяется в предположении, что число столбцов матрицы равно числу строк матрицы .

Произведением двух матриц и , где , заданных в определенном порядке , называется матрица , элементы которой определяются по следующему правилу:

. (4.2)

Иначе говоря, элементы матрицы-произведения определяются следующим образом: элемент i-й строки и k-го столбца матрицы равен сумме произведений элементов i-й строки матрицы на соответствующие элементы k-го столбца матрицы .

Пример 2.1. Найти произведение матриц и .

Решение. Имеем: матрица размера , матрица размера , тогда произведение существует и элементы матрицы равны

, , ,

, , .

, а произведение не существует.

Пример 2.2. В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины , и , причем доставка единицы продукции с каждого молокозавода в магазин стоит 50 ден. ед., в магазин ‑ 70, а в ‑ 130 ден. ед. Подсчитать ежедневные транспортные расходы каждого завода.

Молокозавод	Магазин
1	20	35	10
2	15	27	8

Решение. Обозначим через матрицу, данную нам в условии, а через ‑ матрицу, характеризующую стоимость доставки единицы продукции в магазины, т.е.,

, .

Тогда матрица затрат на перевозки будет иметь вид:

.

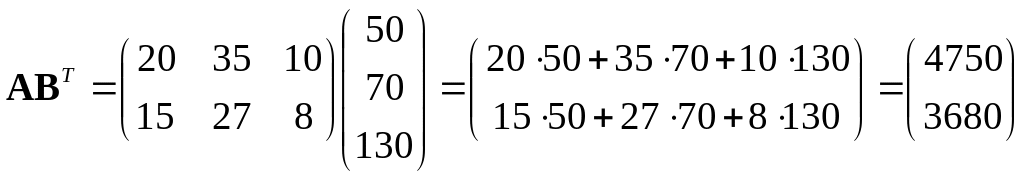Итак, первый завод ежедневно тратит на перевозки 4750 ден. ед., второй ‑ 3680 ден.ед.