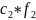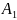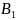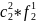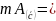Решение:
Дана
многофакторная (сложная) мультипликативная
модель К= ;
;
Критерии ранжирования:
1. количественные факторы анализируются раньше качественных;
2. качественные факторы среди последнего рассматриваются в 1-ю очередь.
Число первичных факторов n=4(Д, р, с, в), входящих в аналитическую формулу расчета результативного показателя;
Число параметров факторной системы: (n+1)=4+1=5 (Д, р, с, К);
Количество этапов детализации n-1=4-1=3.
Информационные данные в полном объеме: по 2-м значениям ( в базисном и анализируемом периодах) для каждого фактора и результативного показателя и темпы роста.
Цель анализа: абсолютное и относительное изменение результативного показателя К от влияния каждого из факторов М, с, р.
±Δ ±m
±m
±Δ ±m
±m
±Δ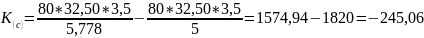 ±m
±m
Задача 2
Формализация задачи Факторная система определена следующими зависимостями: А=(В1+В2)*[f1*c1+f2*c2]; B=B1+B2; A=A1+A2; A=B*c; c=∑fi*ci Исходная информация:
Определить: 1.Абсолютное отклонение результативного показателя А от влияния факторов с1, f2; 2.Относительное отклонение результативного показателя А от влияния каждого из факторов: В, f1, с. Выполнить аналитические проверки полученных результатов. Ф
А В 


1 2
1 1
1 1
1 2
|
С А хема взаимосвязи2 1 В 

2 2 1 1 1
1 В1 с 

В2

С А хема взаимосвязи1 1 
2 2 1 1 1
2
2 1 А1 В1 с1 

А2 В2 
с2 
|
А цп лгоритм решения
ср 
Δ кор 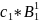
стр 
± ду Δ Δ
Δ
 Δ
Δ
ов [нет, субфактор не в обр. зав.][нет]
[нет данных] ср
цп
кор Δ
стр 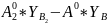
± ду Δ Δ
Δ =
Δ
=
Δ
ов [нет, субфактор не в обр. зав.][нет]
цп [нет]
ср [нет]
кор [нет]
стр [нет]
3кф ду  [нет]
[нет]
[нет] цп
ср [нет]
кор [нет]
стр [нет]
ду [нет]
ов 
[нет]
кор ср [нет]
стр [нет][нет]
ду [нет]
3кф 
|
Пояснение Результативный показатель в данной факторной системе выражен в простой прямой мультипликативной связи. Но в факторной системе присутствуют также аддитивные связи, и есть наличие структурного коэффициента. Способ долевого распределения нигде не может быть применён, исходя из условия.
Δ При нахождении относительного изменения мы можем использовать способ относительных величин и с помощью 3-компонентной формулы.
|