
- •Часть 1
- •Оглавление
- •Введение
- •1. Источники и причины погрешностей математической модели
- •Погрешность математической модели
- •Погрешность исходных данных
- •Погрешность численного метода
- •Погрешность проведения расчетов на вычислительных машинах
- •Погрешности округления чисел в эвм
- •Погрешность результатов вычисления арифметических операций
- •“Потеря порядка” и “переполнение” при проведении вычислений на эвм
- •Машинная реализация вычислений
- •Контрольные вопросы и задания
- •2. Системы линейных алгебраических уравнений
- •Прямые методы решения
- •Метод Гаусса
- •Определение числа операций алгоритма метода Гаусса
- •Вычисление определителя матрицы
- •Построение обратной матрицы
- •Метод квадратного корня
- •Определение числа операций алгоритма метода квадратного корня
- •Устойчивость системы линейных алгебраических уравнений
- •Итерационные методы решения
- •Метод Якоби1
- •Метод Зейделя1
- •Сходимость итерационных методов
- •Скорость сходимости
- •Полиномы Чебышёва1
- •Итерационный метод с чебышёвским набором параметров
- •Неявный метод с чебышёвским набором параметров
- •Метод минимальных невязок
- •Метод минимальных поправок
- •Метод скорейшего спуска
- •Неявный метод скорейшего спуска
- •Контрольные вопросы и задания
- •3.НелинейныЕ уравнения
- •Методы вычисления корней нелинейного уравнения1 Метод половинного деления2
- •Метод простых итераций
- •Метод Ньютона2
- •Модификации метода Ньютона
- •Системы нелинейных уравнений
- •Метод простых итераций
- •Метод релаксации
- •Метод Ньютона
- •Нелинейный вариант метода Якоби
- •Нелинейный вариант метода Зейделя
- •Контрольные вопросы и задания
- •Интерполяция степенными функциями
- •Интерполяционный многочлен Ньютона
- •Интерполяционная формула Лагранжа
- •Погрешность полинома Ньютона (Лагранжа)
- •Сходимость интерполяционного процесса
- •Интерполяционный многочлен Эрмита1
- •Интерполяция сплайнами
- •Построение кубического сплайна
- •Сходимость процесса интерполяции кубическими сплайнами
- •Наилучшее приближение в гильбертовом пространстве
- •Метод наименьших квадратов
- •Контрольные вопросы и задания
- •5. Алгебраическая проблема собственных значений
- •Устойчивость собственных значений и векторов
- •Определение собственных значений и векторов Метод интерполяции
- •Трехдиагональные матрицы
- •Поиск собственных векторов
- •Частичная проблема собственных значений
- •Метод линеаризации
- •Степенной метод
- •Метод обратных итераций
- •Контрольные вопросы и задания
- •6.Численное дифференцирование Конечно-разностная аппроксимация
- •Применение интерполяционных формул
- •Контрольные вопросы и задания
- •7.Численное интегрирование
- •Формула прямоугольников
- •Формула трапеций
- •Формула Симпсона1
- •Формула Эйлера1
- •Оценка погрешности методом Рунге2
Определение числа операций алгоритма метода квадратного корня
Подсчитаем число операций умножения и деления, необходимых для реализации алгоритма метода квадратного корня.
1. Факторизация исходной матрицы, то есть вычисление матриц S и D:
![]() ;
;
2. Выполнение “обратного” хода:
![]() ;
;
3. Вычисление m раз значений квадратных корней.
Общее количество операций равно
![]() ,
или приблизительно
,
или приблизительно
![]() ,
что практически в два раза меньше, чем
число операций в алгоритме метода
Гаусса.
,
что практически в два раза меньше, чем
число операций в алгоритме метода
Гаусса.
Пример 2.1. Рассмотрим решение системы двух линейных алгебраических уравнений методом квадратного корня:
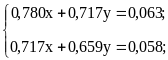
![]()
![]()
1.
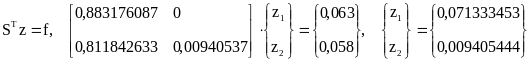 ;
;
2.
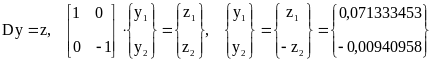 ;
;
3.
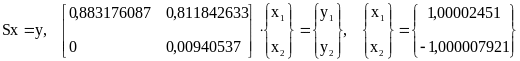 .
.
Точное решение задачи :
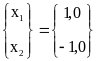 .
.
Устойчивость системы линейных алгебраических уравнений
Для оценки влияния изменения (возмущения) правой части f и матрицы коэффициентов А на решение x системы линейных алгебраических уравнений Ax = f введем линейное пространство H векторов размерности m, в котором определим норму, удовлетворяющую условиям [8]:
![]()
В пространстве Н в качестве нормы вектора могут быть взяты определения “кубической” и “сферической” норм [9]:
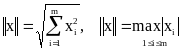 .
.
Определим норму матрицы (оператора):
![]() .
.
Из последнего определения, в частности, следуют известные соотношения:
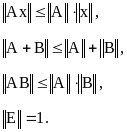
Здесь Е - тождественный оператор,
![]() .
.
В качестве нормы матрицы А может быть взято определение [8]:
![]() ,
,
либо определение [9]:
![]() .
.
Пусть
![]() -
“возмущенная” правая часть системы
уравнений. Оценим изменение решения
-
“возмущенная” правая часть системы
уравнений. Оценим изменение решения
![]() как следствие изменения правой части
как следствие изменения правой части
![]() .
.
Система уравнений Ax=f называется
устойчивой по правой части, если
![]() - положительная константа.
- положительная константа.
Это, в частности, означает, что
![]() при
при
![]() ,
то есть имеется непрерывная зависимость
решения от правой части.
,
то есть имеется непрерывная зависимость
решения от правой части.
Пусть определитель матрицы А отличен
от нуля. В этом случае существует обратная
матрица
![]() .
В силу линейности системы алгебраических
уравнений имеем:
.
В силу линейности системы алгебраических
уравнений имеем:
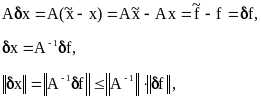
отсюда следует
![]() (2.7)
(2.7)
и роль константы М может выполнять
![]() .
Чем ближе значение det(A) к нулю, тем больше
величина
,
тем значительнее отклонение x
при возмущении f
.
.
Чем ближе значение det(A) к нулю, тем больше
величина
,
тем значительнее отклонение x
при возмущении f
.
Из уравнения Ax = f следует оценка
![]() .
.
Перемножая два последних неравенства, получаем
![]() ,
,
![]() ,
,
где
![]() - число обусловленности матрицы А,
характеризующее зависимость относительной
погрешности решения системы уравнений
от относительного “возмущения” правой
части. Очевидно, что
- число обусловленности матрицы А,
характеризующее зависимость относительной
погрешности решения системы уравнений
от относительного “возмущения” правой
части. Очевидно, что
![]() .
.
Пример 2.2. Рассмотрим систему уравнений
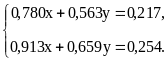
Определитель этой системы уравнений
![]() отличен от 0, хотя и мал. Матрица
коэффициентов представляется в виде
отличен от 0, хотя и мал. Матрица
коэффициентов представляется в виде
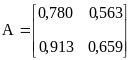 .
.
Вычисление обратной матрицы приводит к значению
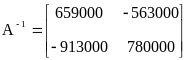 .
.
Нетрудно убедиться, что определитель обратной матрицы принимает значение
![]() .
.
При использовании для вычисления нормы матрицы выражения
получаем для рассматриваемого случая:
![]()
Теперь можно оценить число обусловленности матрицы А, то есть показатель устойчивости решения при возмущении правой части системы уравнений:
![]() .
.
Рассмотрим случай одновременного возмущения и правой части f, и матрицы коэффициентов A:
![]() .
.
Для получения полной оценки погрешности решения системы алгебраических уравнений необходимо рассмотреть вспомогательное утверждение:
Лемма 2.1. Пусть С - квадратная матрица,
![]() ;
Е - единичная матрица. Тогда существует
;
Е - единичная матрица. Тогда существует
![]() ,
причем
,
причем
![]() .
.
Доказательство
Для любого x имеет место неравенство
![]() , (2.8)
, (2.8)
где
![]() - по условию леммы.
- по условию леммы.
Рассмотрим однородное уравнение (E + C)x = 0. Из неравенства (2.8) следует
![]() ,
,
что возможно лишь при
![]() ,
откуда следует, что x = 0 . Иными словами,
однородное уравнение (E + C)x = 0 имеет
только тривиальное решение. Но это
означает, что определитель det(E + C) не
равен нулю, то есть существует обратная
матрица
.
,
откуда следует, что x = 0 . Иными словами,
однородное уравнение (E + C)x = 0 имеет
только тривиальное решение. Но это
означает, что определитель det(E + C) не
равен нулю, то есть существует обратная
матрица
.
Теперь рассмотрим уравнение
(E + C)x = y,
имеющее решением
![]() .
С помощью выражения (2.8) получаем
.
С помощью выражения (2.8) получаем
![]() ,
,
![]() .
.
Последним неравенством воспользуемся для подсчета нормы
![]() .
.
Что и требовалось доказать.
Теорема 2.3. Пусть матрица А имеет обратную и выполнено условие
![]() .
.
Тогда матрица
![]() имеет обратную и справедлива оценка
погрешности
имеет обратную и справедлива оценка
погрешности
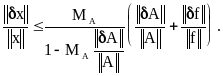
Доказательство
![]() .
.
Оценим норму матрицы С с использованием условия теоремы:
![]() .
.
В силу того, что матрица С удовлетворяет условию леммы 2.1, существует матрица . Поскольку
![]() ,
,
то
![]() существует в силу существования матриц
и
.
существует в силу существования матриц
и
.
Теперь определим отклонение возмущенного решения от исходного:
![]() .
.
Учитывая, что
![]() ,
получаем
,
получаем
![]() ,
,
откуда можно оценить норму
![]() .
.
Оценим порознь слагаемые в правой части этого неравенства:
![]() ;
;
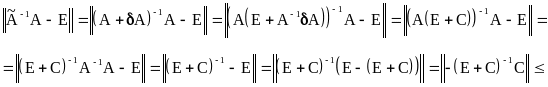
![]() .
.
Подставим полученные оценки в исходную формулу:
![]() .
.
Учитывая, что
![]() ,
,
имеем
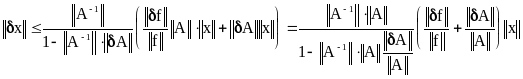 .
.
Вспоминая, что , получаем доказываемое утверждение теоремы
