Определение числа операций алгоритма метода Гаусса

Подсчитаем число операций умножения и деления (наиболее длительные операции при вычислениях на ЭВМ), необходимое для реализации алгоритма метода Гаусса.

1. Вычисление коэффициентов (сумма членов арифметической прогрессии):

.

2. Вычисление коэффициентов (сумма слагаемых арифметической прогрессии 2-го порядка [6]):

.

3. Вычисление значений :

.

4. Вычисление значений производится m раз.

5. Вычисление при “обратном ходе” метода Гаусса:

.

Общее количество операций умножения и деления определяется суммой всех определенных выше выражений:

.

Иными словами, количество операций умножения и деления приблизительно пропорционально , что и определяет затраты на выполнение метода Гаусса.

Вычисление определителя матрицы

Вычитание строк в методе Гаусса (образование линейных комбинаций уравнений) не изменяет значения определителя матрицы [7]. Знак определителя может измениться лишь при использовании процедуры выбора “главного” элемента, когда производится перестановка строк (столбцов) преобразуемой матрицы. В результате выполнения всех необходимых преобразований метода Гаусса определитель исходной матрицы может быть вычислен достаточно просто:

.

Здесь учтено, что L и U - треугольные матрицы и, кроме того, матрица U содержит только единицы на главной диагонали.

Таким образом, сохраняя значения коэффициентов, расположенных после преобразования уравнений (до операции деления коэффициентов строки на первый ненулевой элемент) на главной диагонали, можно вычислить определитель исходной матрицы.

Построение обратной матрицы

Пусть - коэффициенты обратной матрицы . Согласно определению

- символ Кронекера¹.

Теперь q-й столбец обратной матрицы можно рассматривать как результат решения системы линейных алгебраических уравнений вида

.

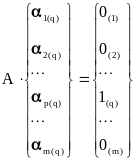Таким образом, для нахождения обратной матрицы необходимо решить m систем линейных алгебраических уравнений с правыми частями, определенными специальным образом. При этом матрицу коэффициентов следует преобразовать лишь один раз, но одновременно преобразовывать m правых частей всех систем уравнений.

Метод квадратного корня

Метод квадратного корня предназначен для решения систем линейных алгебраических уравнений вида Ax = f с симметричной матрицей коэффициентов .

Метод основан на разложении матрицы коэффициентов А в произведение

, (2.4)

где S - верхняя треугольная матрица с положительными значениями на главной диагонали; D - диагональная матрица со значениями +1 или -1.

Согласно теореме 2.1 при неравенстве нулю всех угловых миноров матрицу А можно разложить в произведение A = LU.

Представим нижнюю треугольную матрицу L с ненулевыми коэффициентами на главной диагонали в виде произведения NK, где N - нижняя треугольная матрица с единицами на главной диагонали, К - диагональная матрица, причем :

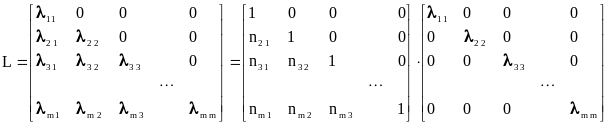
После перемножения матриц N и K получаем систему линейных уравнений относительно величин :

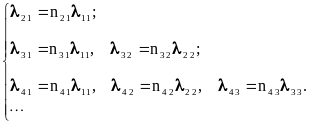
Очевидно, что

С учетом этого коэффициенты матриц N и K можно представить в общем виде

;

.

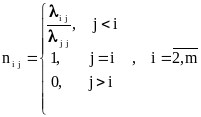Теперь матрицу А можно представить разложением

A = NKU. (2.5)

Благодаря симметрии матрицы А имеет место равенство , что позволяет произвести следующие преобразования:

,

,

,

.

В силу того, что являются диагональными матрицами, - нижние треугольные, - верхние треугольные, в левой части последнего равенства находится нижняя треугольная матрица, а в правой части - верхняя треугольная. Равенство возможно лишь при условии, что и в левой, и в правой частях этого тождества расположены диагональные матрицы.

Матрицы имеют единицы на главной диагонали; следовательно, их произведение также содержит единичную главную диагональ, то есть

.

Отсюда следует, что соотношение (2.5) можно переписать в виде

.

Далее, представим матрицу K в виде

,

где

.

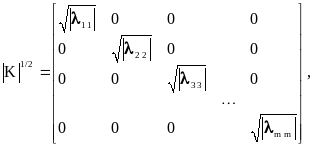
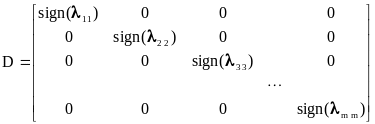Сравнивая теперь соотношение с формулой (2.4), получаем для матрицы S выражение , то есть верхнюю треугольную матрицу с положительными элементами на главной диагонали. Таким образом, конструктивно показано разложение (2.4).

Обозначим , тогда алгоритм метода квадратного корня можно рассматривать как последовательность трех процессов:

, то есть вычисление решения z системы уравнений с нижней треугольной матрицей;

2) Dy = z , вычисление решения системы уравнений с диагональной матрицей;

3) Sx = y , определения из системы уравнений с верхней треугольной матрицей искомого решения.

Построим разложение вида (2.4) для симметричной матрицы третьего ранга:

.

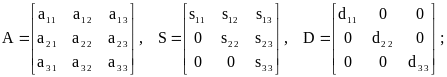
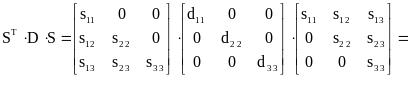
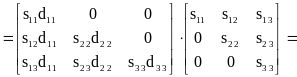
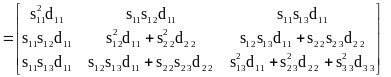Положим , тогда из уравнения получим .

Далее, из уравнения следует, что

.

В силу условия и теоремы 2.2 можно ожидать, что . Аналогично можно вычислить

;

.

Полагая , получим

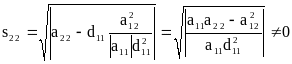
- в силу упомянутого условия .

;

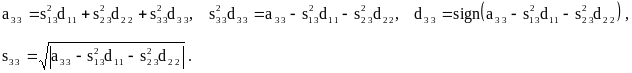
Нетрудно убедиться, что также .

Рассмотрим процедуру построения матриц S и D в случае произвольного числа уравнений m.

Верхняя треугольная матрица по определению имеет нулевые элементы:

. (2.6)

Диагональная матрица D может быть определена формально с использованием символа Кронекера . Теперь можно подсчитать результат перемножения матриц:

Из последнего выражения с учетом соотношения (2.6) получаем систему алгебраических уравнений:

.

При i = j получаем соотношения для вычисления диагональных значений матриц S и D:

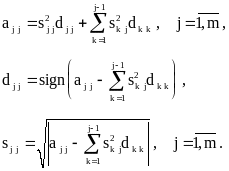
“Наддиагональные” элементы матрицы S определяются по формулам

.
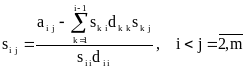