
- •Часть 1
- •Оглавление
- •Введение
- •1. Источники и причины погрешностей математической модели
- •Погрешность математической модели
- •Погрешность исходных данных
- •Погрешность численного метода
- •Погрешность проведения расчетов на вычислительных машинах
- •Погрешности округления чисел в эвм
- •Погрешность результатов вычисления арифметических операций
- •“Потеря порядка” и “переполнение” при проведении вычислений на эвм
- •Машинная реализация вычислений
- •Контрольные вопросы и задания
- •2. Системы линейных алгебраических уравнений
- •Прямые методы решения
- •Метод Гаусса
- •Определение числа операций алгоритма метода Гаусса
- •Вычисление определителя матрицы
- •Построение обратной матрицы
- •Метод квадратного корня
- •Определение числа операций алгоритма метода квадратного корня
- •Устойчивость системы линейных алгебраических уравнений
- •Итерационные методы решения
- •Метод Якоби1
- •Метод Зейделя1
- •Сходимость итерационных методов
- •Скорость сходимости
- •Полиномы Чебышёва1
- •Итерационный метод с чебышёвским набором параметров
- •Неявный метод с чебышёвским набором параметров
- •Метод минимальных невязок
- •Метод минимальных поправок
- •Метод скорейшего спуска
- •Неявный метод скорейшего спуска
- •Контрольные вопросы и задания
- •3.НелинейныЕ уравнения
- •Методы вычисления корней нелинейного уравнения1 Метод половинного деления2
- •Метод простых итераций
- •Метод Ньютона2
- •Модификации метода Ньютона
- •Системы нелинейных уравнений
- •Метод простых итераций
- •Метод релаксации
- •Метод Ньютона
- •Нелинейный вариант метода Якоби
- •Нелинейный вариант метода Зейделя
- •Контрольные вопросы и задания
- •Интерполяция степенными функциями
- •Интерполяционный многочлен Ньютона
- •Интерполяционная формула Лагранжа
- •Погрешность полинома Ньютона (Лагранжа)
- •Сходимость интерполяционного процесса
- •Интерполяционный многочлен Эрмита1
- •Интерполяция сплайнами
- •Построение кубического сплайна
- •Сходимость процесса интерполяции кубическими сплайнами
- •Наилучшее приближение в гильбертовом пространстве
- •Метод наименьших квадратов
- •Контрольные вопросы и задания
- •5. Алгебраическая проблема собственных значений
- •Устойчивость собственных значений и векторов
- •Определение собственных значений и векторов Метод интерполяции
- •Трехдиагональные матрицы
- •Поиск собственных векторов
- •Частичная проблема собственных значений
- •Метод линеаризации
- •Степенной метод
- •Метод обратных итераций
- •Контрольные вопросы и задания
- •6.Численное дифференцирование Конечно-разностная аппроксимация
- •Применение интерполяционных формул
- •Контрольные вопросы и задания
- •7.Численное интегрирование
- •Формула прямоугольников
- •Формула трапеций
- •Формула Симпсона1
- •Формула Эйлера1
- •Оценка погрешности методом Рунге2
Погрешность проведения расчетов на вычислительных машинах
Оценка погрешности результата вычисления
при заданной ошибке в представлении
данных может быть проведена следующим
образом. Пусть x - точное значение, а
![]() -
приближенное значение той же переменной.
Обозначим абсолютную погрешность
в определении переменной разностью
-
приближенное значение той же переменной.
Обозначим абсолютную погрешность
в определении переменной разностью
![]() .
.
Поскольку точное значение x неизвестно,
введем “верхнюю” оценку
для величины погрешности:
![]() .
Определим также величину относительной
погрешности
.
Определим также величину относительной
погрешности
![]() .
.
Абсолютная погрешность делится на приближенное значение переменной, поскольку ее точное значение неизвестно.
Погрешности округления чисел в эвм
круглением будем называть операцию замены заданного числа другим числом, первые S значащих цифр которого совпадают с соответствующими цифрами исходного числа, а начиная с S+1 разряда содержат нули.
Многие практические способы округления чисел выполняют отбрасывание “лишних” разрядов, хотя возможны варианты, при которых в “младший” разряд округленного числа, в зависимости от ситуации, может добавляться единица.
Пусть, например, x=123456789, тогда при S=7
округленное число принимает значение
![]() .
В этом случае погрешность округления
равна
.
В этом случае погрешность округления
равна
![]() ,
то есть не превышает единицы (с
соответствующим порядком) в младшем
разряде округленного числа.
,
то есть не превышает единицы (с
соответствующим порядком) в младшем
разряде округленного числа.
Всякое вещественное число в компьютере
представляется в нормализованном виде
x = apb, где p -
основание, b - показатель степени (целые
числа), a - мантисса (вещественное число).
Для определенности и однозначности
будем считать p=10,
![]() .
Ошибки округления появляются при
хранении именно мантиссы вещественного
числа. В представлении чисел на
персональных компьютерах IBM достоверными
могут быть 7 значащих цифр (для хранения
числа отводится 4 байта оперативной
памяти), 15 цифр (8 байт) или 19 (10 байт).
.
Ошибки округления появляются при
хранении именно мантиссы вещественного
числа. В представлении чисел на
персональных компьютерах IBM достоверными
могут быть 7 значащих цифр (для хранения
числа отводится 4 байта оперативной
памяти), 15 цифр (8 байт) или 19 (10 байт).
Рассмотрим оценки погрешности округления
при S=7. Округленное число представляется
в виде
![]() ,
где под символом X может пониматься
любая цифра от 0 до 9. Очевидно, что
абсолютная погрешность определяется
значением
,
где под символом X может пониматься
любая цифра от 0 до 9. Очевидно, что
абсолютная погрешность определяется
значением
![]() .
.
Модуль относительной погрешности
![]() .
.
Для некоторых частных случаев погрешность представления вещественных чисел оценивается:
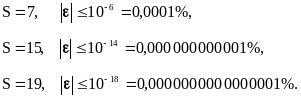
Для всех чисел, представимых в электронно-вычислительной машине, относительная погрешность одна и та же, что очень существенно при получении оценок погрешностей математических моделей.
Погрешность результатов вычисления арифметических операций
Оценим погрешность результата сложения двух чисел, заданных с ошибкой:
![]() .
.
Аналогично определяется погрешность результата вычитания:
![]() .
.
Для определения абсолютных погрешностей операций умножения и деления двух чисел проведем соответствующие выкладки:
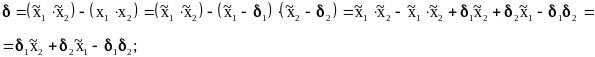
![]() .
.
Оценим относительные погрешности результатов умножения и деления:
![]() ,
,
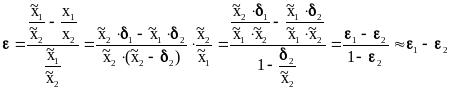 .
.
В последних выражениях учитывается,
что величины
![]() .
.
Таким образом, при выполнении арифметических операций сложения и вычитания складываются (вычитаются) абсолютные погрешности, а при умножении и делении - относительные погрешности.
“Потеря порядка” и “переполнение” при проведении вычислений на эвм
Пусть - наименьшее
положительное число, представимое в
ЭВМ;
![]() при использовании 4 байт, и
при использовании 4 байт, и
![]() при 8-байтовом представлении вещественной
переменной. Это означает, что все
действительные числа из интервала
при 8-байтовом представлении вещественной
переменной. Это означает, что все
действительные числа из интервала
![]() нельзя представить в ЭВМ в нормализованном
виде. В этом случае приближение истинного
числа в компьютере равно
нельзя представить в ЭВМ в нормализованном
виде. В этом случае приближение истинного
числа в компьютере равно
![]() .
Но это означает, что имеет место
катастрофическая потеря точности
арифметических вычислений:
.
Но это означает, что имеет место
катастрофическая потеря точности
арифметических вычислений:
![]() .
.
С другой стороны, пусть
- наибольшее положительное число,
представимое в ЭВМ. Все действительные
числа |x| >
нельзя представить в нормализованной
форме. Приближение числа x определяется
как
![]() .
Очевидно, что и в этом случае имеет место
потеря точности:
.
Очевидно, что и в этом случае имеет место
потеря точности:
![]() .
.
