Наилучшее приближение в гильбертовом пространстве

Рассмотрим линейное нормированное пространство H, в котором задана конечная система линейно-независимых элементов . Требуется заменить некоторый элемент линейной комбинацией

, (4.26)

где  - обобщенный многочлен.

Задача о наилучшем приближении заключается в поиске среди множества линейных комбинаций вида (4.26) такой, для которой отклонение было бы наименьшим. Такой элемент (обобщенный полином) является элементом наилучшего приближения.

Пусть H - гильбертово пространство с нормой, порожденной скалярным произведением

,

.

Рассмотрим отклонение приближения (4.26) от элемента f :

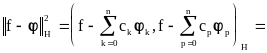
(4.27)

Введем обозначения:

A - матрица с компонентами ;

c - вектор коэффициентов ;

- вектор .

Скалярное произведение векторов определим обычным образом:

.

Теперь выражение (4.27) можно представить следующим образом:

. (4.28)

Очевидно, что поиск элемента наилучшего приближения сводится теперь к поиску минимума функционала

, (4.29)

поскольку слагаемое в выражении (4.28) от параметров не зависит.

Исследуем свойства матрицы A. Поскольку , то очевидно, что матрица A симметрична.

Если положить f = 0, то из соотношения (4.28) можно получить:

.

Если для какого-либо имеет место равенство , то в силу получаем, что , и из условия линейной независимости следует : . Но это означает, что , то есть матрица А является положительно определенной.

Теорема 4.4. Если А - симметричная положительно определенная матрица, - заданный вектор, то функционал (4.29) имеет единственную точку минимума тогда и только тогда, когда вектор удовлетворяет системе линейных алгебраических уравнений

. (4.30)

Доказательство. В силу положительной определенности матрица А имеет определитель, отличный от нуля, то есть система уравнений (4.30) разрешима и имеет единственное решение.

Достаточность теоремы. Пусть является решением системы уравнений (4.30). Для произвольного вектора v, согласно определению (4.29), имеет место:

.

Учитывая симметрию матрицы A и вид функционала (4.29), запишем

.

Принимая во внимание выражение (4.30), окончательно получаем

.

С учетом положительной определенности матрицы А последнее выражение приводит к неравенству , но это и означает минимальность функционала (4.29) в точке .

Необходимость. Пусть теперь вектор доставляет минимум функционалу (4.29).

Воспользуемся полученным выше равенством

.

Положим - произвольный вектор,  - скаляр; тогда

.

Полученное выражение теперь можно рассматривать как скалярную функцию

аргумента .

В силу допущения о минимальности функционала (4.29) имеем , то есть . Это, в свою очередь означает, что =0 доставляет минимум функции g(), откуда следует

,

.

Поскольку последнее равенство справедливо , получаем , что и требовалось доказать.

В компонентной записи система линейных алгебраических уравнений выглядит следующим образом:

. (4.31)

Алгоритм определения элемента наилучшего приближения:

- вычисление коэффициентов матрицы ;

- вычисление значений правых частей ;

- решение системы уравнений (4.31);

- построение .

В случае ортонормированности системы построение приближения значительно упрощается, поскольку в этом случае и коомпоненты вектора определяются сразу:

.

В этом случае погрешность приближения может быть оценена следующим образом:

Разложение носит название многочлена Фурье¹, а - коэффициенты Фурье.

На рис. 4.6 приведены графики приближения | x | c помощью степенных рядов.

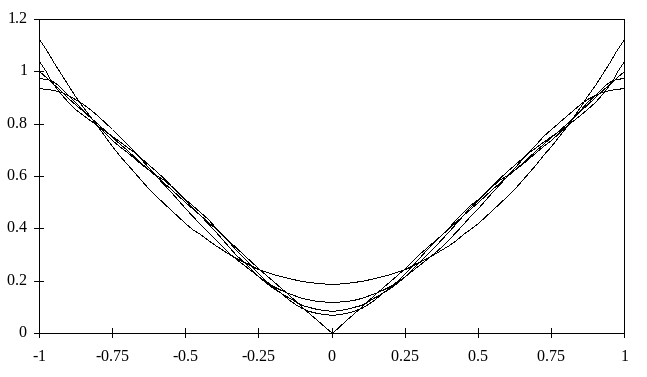Рис. 4.6. Построение наилучшего приближения функции | x | с помощью полиномов P_n