
- •Часть 1
- •Оглавление
- •Введение
- •1. Источники и причины погрешностей математической модели
- •Погрешность математической модели
- •Погрешность исходных данных
- •Погрешность численного метода
- •Погрешность проведения расчетов на вычислительных машинах
- •Погрешности округления чисел в эвм
- •Погрешность результатов вычисления арифметических операций
- •“Потеря порядка” и “переполнение” при проведении вычислений на эвм
- •Машинная реализация вычислений
- •Контрольные вопросы и задания
- •2. Системы линейных алгебраических уравнений
- •Прямые методы решения
- •Метод Гаусса
- •Определение числа операций алгоритма метода Гаусса
- •Вычисление определителя матрицы
- •Построение обратной матрицы
- •Метод квадратного корня
- •Определение числа операций алгоритма метода квадратного корня
- •Устойчивость системы линейных алгебраических уравнений
- •Итерационные методы решения
- •Метод Якоби1
- •Метод Зейделя1
- •Сходимость итерационных методов
- •Скорость сходимости
- •Полиномы Чебышёва1
- •Итерационный метод с чебышёвским набором параметров
- •Неявный метод с чебышёвским набором параметров
- •Метод минимальных невязок
- •Метод минимальных поправок
- •Метод скорейшего спуска
- •Неявный метод скорейшего спуска
- •Контрольные вопросы и задания
- •3.НелинейныЕ уравнения
- •Методы вычисления корней нелинейного уравнения1 Метод половинного деления2
- •Метод простых итераций
- •Метод Ньютона2
- •Модификации метода Ньютона
- •Системы нелинейных уравнений
- •Метод простых итераций
- •Метод релаксации
- •Метод Ньютона
- •Нелинейный вариант метода Якоби
- •Нелинейный вариант метода Зейделя
- •Контрольные вопросы и задания
- •Интерполяция степенными функциями
- •Интерполяционный многочлен Ньютона
- •Интерполяционная формула Лагранжа
- •Погрешность полинома Ньютона (Лагранжа)
- •Сходимость интерполяционного процесса
- •Интерполяционный многочлен Эрмита1
- •Интерполяция сплайнами
- •Построение кубического сплайна
- •Сходимость процесса интерполяции кубическими сплайнами
- •Наилучшее приближение в гильбертовом пространстве
- •Метод наименьших квадратов
- •Контрольные вопросы и задания
- •5. Алгебраическая проблема собственных значений
- •Устойчивость собственных значений и векторов
- •Определение собственных значений и векторов Метод интерполяции
- •Трехдиагональные матрицы
- •Поиск собственных векторов
- •Частичная проблема собственных значений
- •Метод линеаризации
- •Степенной метод
- •Метод обратных итераций
- •Контрольные вопросы и задания
- •6.Численное дифференцирование Конечно-разностная аппроксимация
- •Применение интерполяционных формул
- •Контрольные вопросы и задания
- •7.Численное интегрирование
- •Формула прямоугольников
- •Формула трапеций
- •Формула Симпсона1
- •Формула Эйлера1
- •Оценка погрешности методом Рунге2
Интерполяционная формула Лагранжа
Идея записи интерполяционного полинома Лагранжа заключается в следующем:
![]() , (4.4)
, (4.4)
то есть в каждой точке x значение полинома
![]() определяется как линейная комбинация
табличных значений.
определяется как линейная комбинация
табличных значений.
Воспользуемся условием (4.1) :
![]() .
.
Отсюда очевидно, что должно выполняться условие
![]() ,
,
то есть на отрезке интерполяции [a, b]
каждая из функций
![]() должна иметь n корней.
должна иметь n корней.
Вполне естественно представить в виде полиномов
![]() ,
,
![]() -
нормировочный коэффициент, определяемый
из условия, что
-
нормировочный коэффициент, определяемый
из условия, что
![]() ,
то есть
,
то есть
![]() .
.
Теперь можно записать полином Лагранжа в общем виде:
![]() . (4.5)
. (4.5)
Погрешность полинома Ньютона (Лагранжа)
Погрешность представления функции полиномом оценим разностью
![]() .
.
Очевидно, что в узлах
![]() погрешность
погрешность
![]() .
.
Для оценки погрешности выберем и
зафиксируем произвольную точку
![]() .
Рассмотрим вспомогательную функцию
.
Рассмотрим вспомогательную функцию
![]() , (4.6)
, (4.6)
K - константа. Очевидно, что
![]() .
Выберем константу К в выражении (4.6) так,
чтобы для выбранного значения x функция
g(x) = 0, то есть
.
Выберем константу К в выражении (4.6) так,
чтобы для выбранного значения x функция
g(x) = 0, то есть
![]() .
.
Пусть функция y(x) имеет (n+1) производную,
то есть является достаточно гладкой
функцией. Согласно построению функция
g(s) имеет не менее (n+2) нулей в точках
![]() .
В этом случае функция
.
В этом случае функция
![]() на отрезке [a,b] имеет не менее (n+1) нулей;
на отрезке [a,b] имеет не менее (n+1) нулей;
![]() - не менее n нулей, и так далее. И, наконец,
- не менее n нулей, и так далее. И, наконец,
![]() имеет хотя бы один корень на отрезке
[a,b]. Иначе говоря,
имеет хотя бы один корень на отрезке
[a,b]. Иначе говоря,
![]() .
В силу определения функции g(s),
.
В силу определения функции g(s),
![]() ,
,
и для точки получаем
![]() .
.
Отсюда следует
![]() .
.
Окончательно,
![]() . (4.7)
. (4.7)
В частном случае, когда y(x) является
полиномом степени n,
![]() и
и
![]() .
Дополнительно можно подобрать такое
распределение узловых точек
,
чтобы минимизировать выражение
.
Дополнительно можно подобрать такое
распределение узловых точек
,
чтобы минимизировать выражение
![]() ,
,
являющееся полиномом степени n со старшим коэффициентом, равным 1. Иначе говоря, получена задача Чебышёва, рассмотренная ранее. Искомый полином имеет на отрезке [a,b] корни
![]() .
.
Оценка модуля полинома, наименее уклоняющего от нуля,
![]() .
.
Оценка погрешности полинома Ньютона (Лагранжа) при использовании узловых точек, соответствующих корням полинома Чебышева, имеет вид
![]() .
.
Сходимость интерполяционного процесса
Множество точек
![]() назовем сеткой на отрезке [a, b] и
обозначим
назовем сеткой на отрезке [a, b] и
обозначим
![]() .
Рассмотрим последовательность сеток
.
Рассмотрим последовательность сеток
![]() Построим на отрезке [a,b] последовательность
полиномов
Построим на отрезке [a,b] последовательность
полиномов
![]() ,
аппроксимирующих с помощью сеток
функцию y(x).
,
аппроксимирующих с помощью сеток
функцию y(x).
Интерполяционный процесс сходится
в точке
![]() ,
если существует предел
,
если существует предел
![]() (определение поточечной сходимости).
(определение поточечной сходимости).
Интерполяционный процесс сходится равномерно на отрезке [a, b], если
![]() .
.
Теорема 4.1 (Фабера1). Какова бы ни была последовательность сеток , найдется непрерывная на [a,b] функция y(x) такая, что последовательность интерполяционных полиномов не сходится к y(x) равномерно на этом отрезке.
На рис. 4.1 приведен пример аппроксимации непрерывной функции f(x) = |x| на последовательности сеток с равноотстоящими узлами.
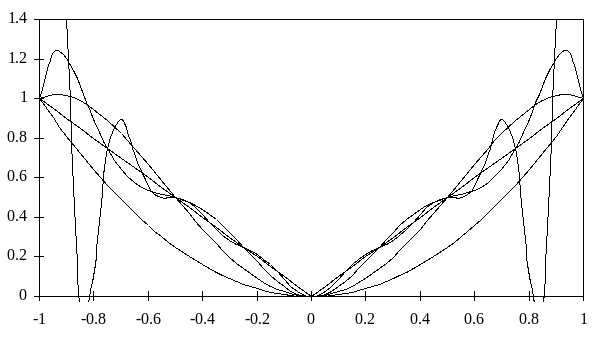
Рис. 4.1. Аппроксимация на отрезке [-1, 1] функции f(x) = |x| полиномами Pn, построенными с использованием равномерных сеток
На рис. 4.2 представлен график погрешности аппроксимации функции f(x) = |x| полиномамм на равномерных сетках в зависимости от числа отрезков сеточной области.
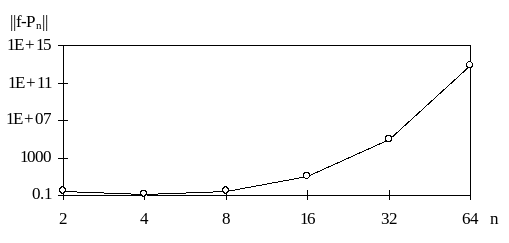
Рис. 4.2. Погрешность аппроксимация на отрезке [-1, 1] функции f(x) = |x| в зависимости от числа отрезков равномерной сетки.
Теорема 4.2. Если функция y(x) непрерывна на отрезке [a,b], то найдется такая последовательность сеток, для которой интерполяционный процесс сходится равномерно на этом отрезке.
На рис. 4.3 приведен пример аппроксимации непрерывной функции f(x) = |x| на последовательности неравномерных (чебышевских) сеток. На рис. 4.4 представлен график погрешности аппроксимации функции f(x) = |x| полиномом Pn на чебышевской сетке в зависимости от числа отрезков сеточной области.
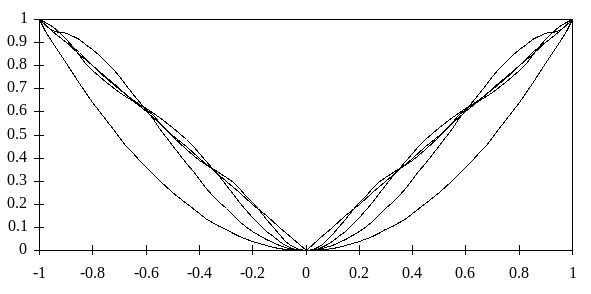
Рис. 4.3. Аппроксимация на отрезке [-1, 1] функции f(x) = |x| полиномами Pn, построенными с использованием чебышёвских сеток
