Системы нелинейных уравнений
Рассмотрим систему m нелинейных алгебраических уравнений:
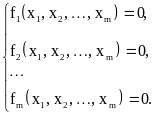
Введем обозначения:
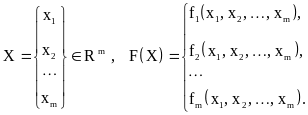
Теперь задача о решении системы нелинейных
алгебраических уравнений может быть
сформулирована следующим образом:
необходимо найти вектор
,
. (3.9)
В общем случае итерационные методы решения системы нелинейных алгебраических уравнений могут быть представлены в канонической форме
, (3.10)
где
-
начальное приближение; числа
и матрицы
,
имеющие обратные, - итерационные
параметры.
Метод простых итераций
Из выражения (3.10) можно получить систему линейных алгебраических уравнений относительно искомых неизвестных:
.
В частном случае стационарного
итерационного метода, когда
,
последнее выражение преобразуется к
виду
.
Иначе говоря, исходная итерационная процедура сводится к схеме метода простых итераций:
. (3.11)
Вектор
,
для которого
,
называется неподвижной точкой
оператора .
Очевидно, что вектор X является решением
уравнения X = (X)
тогда и только тогда, когда он является
неподвижной точкой.
Оператор
является сжимающим на множестве
с коэффициентом сжатия С, если
имеет место
.
Теорема 3.3. Пусть оператор
определен на множестве
и является сжимающим на этом множестве
с коэффициентом сжатия С , причем
.
Тогда в А оператор
имеет единственную неподвижную точку
и итерационный метод (3.11) сходится к
при любом начальном
.
Имеет место оценка погрешности:
.
Доказательство этой теоремы изложено в книгах [4, 9].
Метод релаксации
Положим в выражении (3.11) матрицу В = Е
(тождественное преобразование), тогда
.
Метод сходится, если
.
В этом случае
.
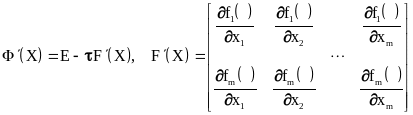Метод Ньютона
Как и ранее, выберем в окрестности
решения
вектор X и воспользуемся формулой Тейлора
для функций
:
,
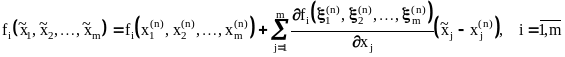где
.
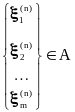С учетом того, что
,
итерационная процедура метода Ньютона
принимает форму
.
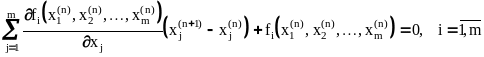В матричной записи последнее соотношение имеет вид:
, (3.12)
где вид матрицы
определен выше. Сравнение формулы (3.12)
с выражением (3.10) позволяет определить
итерационные параметры:
.
Соотношение (3.12) позволяет построить вычислительный итерационный алгоритм:
.
Теорема 3.4. Пусть выполнены условия:
1. Оператор F(X) определен в замкнутом
шаре
,
дважды дифференцируем там, при этом
вторая производная ограничена
.
2.
имеет обратный оператор, для нормы
которого выполнена оценка
.
3. Для начального приближения
верно неравенство
.
4. Величины M, D, S удовлетворяют условию
.
5. Для числа r верно неравенство
.
Тогда:
- в заданном шаре радиуса r уравнение F(X) = 0 имеет решение;
- в вычислительном процессе Ньютона
(3.12) приближение
может быть построено при любом значении
n ; все
принадлежат шару и последовательность
сходится
к решению
уравнения;
- для приближения верна оценка:
,
где
есть наименьший корень уравнения
,
-
приближение к нему, построенное при
начальном приближении
.
Доказательство теоремы 3.4 приведено в книге [4].
В качестве модификации метода Ньютона (3.12) может рассматриваться вариант
,
при котором матрица формируется и обращается лишь один раз для начального приближения .