
- •Часть 1
- •Оглавление
- •Введение
- •1. Источники и причины погрешностей математической модели
- •Погрешность математической модели
- •Погрешность исходных данных
- •Погрешность численного метода
- •Погрешность проведения расчетов на вычислительных машинах
- •Погрешности округления чисел в эвм
- •Погрешность результатов вычисления арифметических операций
- •“Потеря порядка” и “переполнение” при проведении вычислений на эвм
- •Машинная реализация вычислений
- •Контрольные вопросы и задания
- •2. Системы линейных алгебраических уравнений
- •Прямые методы решения
- •Метод Гаусса
- •Определение числа операций алгоритма метода Гаусса
- •Вычисление определителя матрицы
- •Построение обратной матрицы
- •Метод квадратного корня
- •Определение числа операций алгоритма метода квадратного корня
- •Устойчивость системы линейных алгебраических уравнений
- •Итерационные методы решения
- •Метод Якоби1
- •Метод Зейделя1
- •Сходимость итерационных методов
- •Скорость сходимости
- •Полиномы Чебышёва1
- •Итерационный метод с чебышёвским набором параметров
- •Неявный метод с чебышёвским набором параметров
- •Метод минимальных невязок
- •Метод минимальных поправок
- •Метод скорейшего спуска
- •Неявный метод скорейшего спуска
- •Контрольные вопросы и задания
- •3.НелинейныЕ уравнения
- •Методы вычисления корней нелинейного уравнения1 Метод половинного деления2
- •Метод простых итераций
- •Метод Ньютона2
- •Модификации метода Ньютона
- •Системы нелинейных уравнений
- •Метод простых итераций
- •Метод релаксации
- •Метод Ньютона
- •Нелинейный вариант метода Якоби
- •Нелинейный вариант метода Зейделя
- •Контрольные вопросы и задания
- •Интерполяция степенными функциями
- •Интерполяционный многочлен Ньютона
- •Интерполяционная формула Лагранжа
- •Погрешность полинома Ньютона (Лагранжа)
- •Сходимость интерполяционного процесса
- •Интерполяционный многочлен Эрмита1
- •Интерполяция сплайнами
- •Построение кубического сплайна
- •Сходимость процесса интерполяции кубическими сплайнами
- •Наилучшее приближение в гильбертовом пространстве
- •Метод наименьших квадратов
- •Контрольные вопросы и задания
- •5. Алгебраическая проблема собственных значений
- •Устойчивость собственных значений и векторов
- •Определение собственных значений и векторов Метод интерполяции
- •Трехдиагональные матрицы
- •Поиск собственных векторов
- •Частичная проблема собственных значений
- •Метод линеаризации
- •Степенной метод
- •Метод обратных итераций
- •Контрольные вопросы и задания
- •6.Численное дифференцирование Конечно-разностная аппроксимация
- •Применение интерполяционных формул
- •Контрольные вопросы и задания
- •7.Численное интегрирование
- •Формула прямоугольников
- •Формула трапеций
- •Формула Симпсона1
- •Формула Эйлера1
- •Оценка погрешности методом Рунге2
Неявный метод с чебышёвским набором параметров
Рассмотрим неявную итерационную схему с положительно определенными матрицами А и В:
![]() . (2.21)
. (2.21)
Эта система уравнений для погрешностей принимает вид
![]() .
.
Указанные свойства матрицы В позволяют
представить ее в виде
![]() .
Тогда предыдущее соотношение можно
представить в форме
.
Тогда предыдущее соотношение можно
представить в форме
![]() .
.
Обозначим
![]() .
Тогда
.
Тогда
![]() ,
,
где
![]() - симметричная положительно определенная
матрица, причем минимальное (максимальное)
собственное значение матрицы
- симметричная положительно определенная
матрица, причем минимальное (максимальное)
собственное значение матрицы
![]() является одовременно и минимальным
(максимальным) собственным значением
для матрицы С.
является одовременно и минимальным
(максимальным) собственным значением
для матрицы С.
Теорема 2.7. Пусть А и В - симметричные
и положительно определенные матрицы.
![]() - наименьшее и наибольшее собственные
значения матрицы
.
Для заданного числа N итераций неявный
чебышёвский метод (2.21) имеет минимальную
погрешность при наборе
,
определенном условиями предыдущей
теоремы, где
- наименьшее и наибольшее собственные
значения матрицы
.
Для заданного числа N итераций неявный
чебышёвский метод (2.21) имеет минимальную
погрешность при наборе
,
определенном условиями предыдущей
теоремы, где
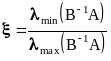 .
.
Удачным выбором матрицы В можно
приблизить значение параметра
к 1, что приведет к понижению погрешности
![]() .
.
Метод минимальных невязок
Погрешность
![]() решения системы линейных алгебраических
уравнений вида1
Ax = f определить невозможно, поскольку
точное решение x неизвестно. Однако
можно оценить невязку
решения системы линейных алгебраических
уравнений вида1
Ax = f определить невозможно, поскольку
точное решение x неизвестно. Однако
можно оценить невязку
![]() ,
,
определяющую, насколько полученное решение не удовлетворяет исходному уравнению.
Рассмотрим явный итерационный метод:
![]() .
.
Определим из этого соотношения величину
![]() :
:
![]() .
.
При использовании итерационной схемы
для (n+1) шага следует так подобрать
итерационный параметр
![]() ,
чтобы при известном
,
чтобы при известном
![]() значение невязки
значение невязки
![]() стало наименьшим.
стало наименьшим.
Оценим невязку для следующего шага:
![]() .
.
Определим, как и ранее, квадрат нормы невязки:
![]()
![]()
![]() .
.
При выводе последнего выражения учтено, что
![]() ,
,
![]() - в силу симметрии матрицы.
- в силу симметрии матрицы.
Полученное соотношение между невязками
на соседних шагах итерационной процедуры
можно рассматривать как функциональную
зависимость
![]() .
Для нахождения значения итерационного
параметра, при котором невязка
.
Для нахождения значения итерационного
параметра, при котором невязка
![]() минимальна, воспользуемся теоремой
Ферма1
:
минимальна, воспользуемся теоремой
Ферма1
:
![]() ,
,
![]() .
.
Оценка невязки получаемого решения:
![]() .
.
Здесь
![]() - наименьшее и наибольшее собственные
значения матрицы А; n - номер итерации.
- наименьшее и наибольшее собственные
значения матрицы А; n - номер итерации.
Метод минимальных поправок
Неявную итерационную схему
![]()
можно представить виде
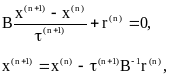
где, как и ранее,
![]() .
Вектор
.
Вектор
![]() назовем поправкой. Очевидно, что
поправка
назовем поправкой. Очевидно, что
поправка
![]() удовлетворяет уравнению
удовлетворяет уравнению
![]() .
.
Предполагая, что В - симметричная положительно определенная матрица, определим норму в виде
![]() .
.
Подсчитаем значение квадрата нормы
поправки
![]() :
:
![]()
![]()
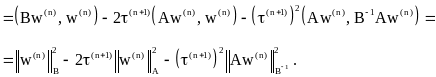
При получении последнего выражения использовались следующие соотношения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Очевидно, что величина
![]() будет минимальной при условии
будет минимальной при условии
![]() ,
,
 .
.
Для реализации метода минимальных
поправок требуется на каждой итерации
решать систему уравнений
![]() ,
откуда находится сама поправка
,
откуда находится сама поправка
![]() .
Кроме этого необходимо определить
решение системы уравнений
.
Кроме этого необходимо определить
решение системы уравнений
![]() ,
а именно, вычислить
,
а именно, вычислить
![]() ,
требующееся для нахождения итерационного
параметра.
,
требующееся для нахождения итерационного
параметра.
Погрешность метода минимальных поправок оценивается следующим образом (с учетом введенного определения нормы):
![]() .
.
Как и ранее,
- наименьшее и наибольшее собственные
значения матрицы
![]() ;
n - номер итерации.
;
n - номер итерации.
