5. Изучение формы кривой распределения.

Кривая распределения характеризует теоретическое (аналитическое) распределение, т.е. распределение, которое получилось бы при полном погашении всех случайных причин, искажающих основную закономерность.

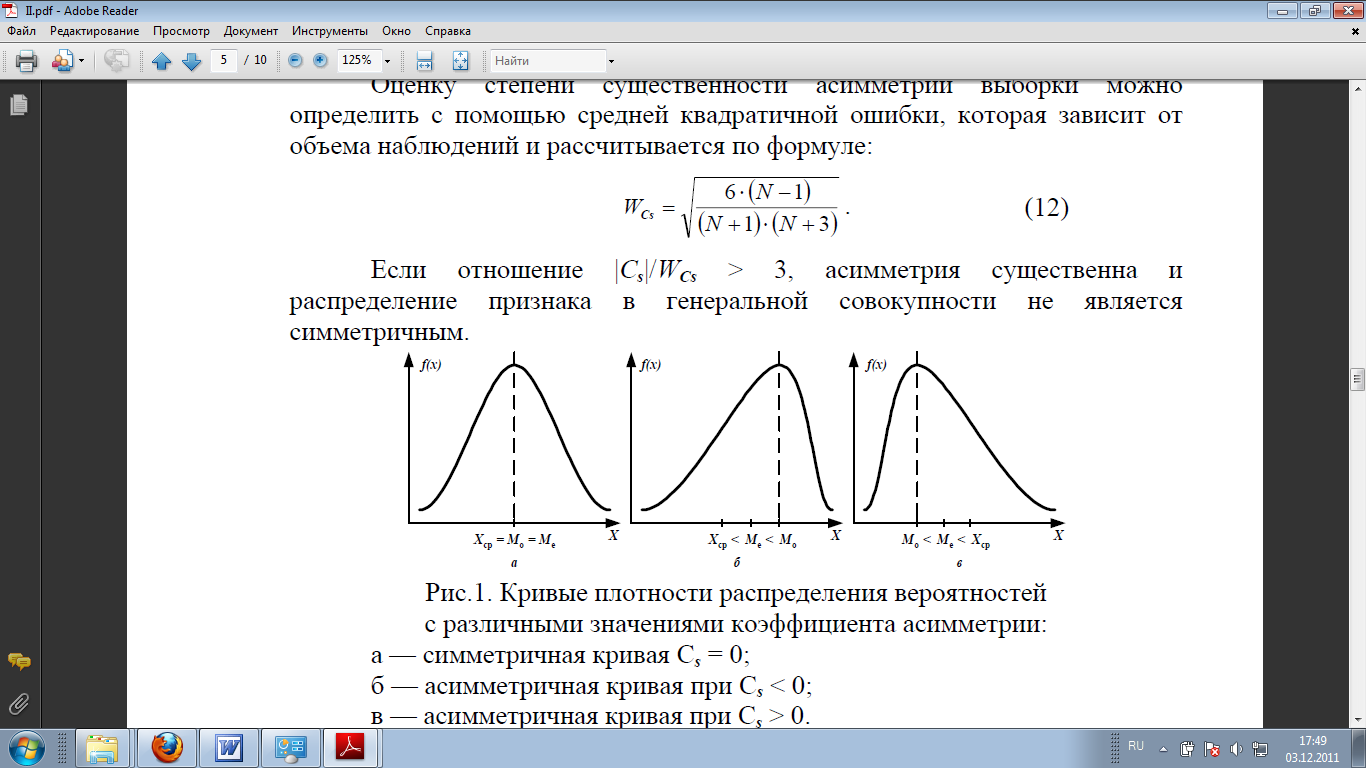
Выявление общего характера распределения предполагает оценку степени его однородности, а также вычисление показателей асимметрии и эксцесса. Для симметричных распределений среднее арифметическое, мода и медиана совпадают, коэффициент асимметрии равен нулю (C_s = 0). При правосторонней (C_s > 0) между показателями центра распределения

существует следующее соотношение М_o < М_е < Х_ср. Отрицательный знак показателя асимметрии (Cs < 0) свидетельствует о наличии левосторонней асимметрии. Между показателями центра распределения в этом случае имеем М_o > М_е > Х_ср.

Полученный коэффициент асимметрии показывает на наличие правосторонней асимметрии:

C_s = 0,26 ; M_o < M_e < X_cp ; 19,57 < 21,49 < 21,65.

M_o M_e X_ср

Кривая плотности распределения вероятности показана на рисунке:

Оценка степени существенности асимметрии определяется при помощи средней квадратической ошибки асимметрии по формуле (12):

(12)

W_Cs=0,41

Если отношение |C_s|/W_Cs < 3, асимметрия несущественна и распределение признака в генеральной совокупности является симметричным.

|C_s|/W_Cs=0,26/0,41=0,63< 3

Вывод: асимметрия не существенна для выборки при подборе генеральной совокупности можно воспользоваться симметричными кривыми распределения.

Величина коэффициента эксцесса отрицательна (С_e = -1,05), значит распределение плосковершинное. Средняя квадратичная ошибка эксцесса рассчитывается по формуле:

(13)

W_Ce= 0,14

Если отношение |C_e|/W_Ce < 3, то эксцесс не свойственен распределению признака в генеральной совокупности.

|C_e|/W_Ce = 1,05/0,14 < 3

Вывод: эксцесс несущественен для выборки, все предпосылки результатов расчетов направлены на подержание искомого аналитического расчета – нормальная кривая распределения.

Далее это будет проверено статистическим критерием согласия Пирсона.

6. Проверка статистических гипотез

Статистические критерии можно разделить на следующие группы: критерии однородности и критерии согласия.

С помощью критериев однородности исследователь пытается на основе отрывочных данных

удлинить ряд данных натурных наблюдений. Экспериментатор проверяет на однородность несколько рядов натурных наблюдений с целью объединения их в один. Необходимость использования критериев однородности обусловлена: стремлением получить более совершенные расчетные параметры кривых распределения (с увеличением объема выборки расчетные статистические величины приобретают количественную стабильность,

увеличивается существенность каждой характеристики, проявляются закономерности распределения случайных величин). Критериев однородности достаточно много. Наиболее распространенными в практических расчетах являются критерии Фишера и Стьюдента

(параметрические критерии, – в основе которых лежит предположение о принадлежности случайных величин к нормальному закону распределения), из непараметрических можно выделить критерий Вилкоксона (нет предположений о законах распределения сравниваемых выборок).

Критерии согласия позволяют подобрать к эмпирическому распределению конкретное теоретическое. Наиболее распространенным в практических расчетах является критерий Пирсона или χ².

Цель использования критериев заключается в определении закономерностей возникновения случайных величин, их свойств, которые определяют сущность прогнозов и играют важную роль в управлении природными явлениями.

Использование критериев согласия преследует цель поиска закона распределения генеральной совокупности, которой принадлежит данная анализируемая выборка. Расчеты проводятся для исходной выборки (X) при N =30. Цель расчетов заключается в следующем: с помощью критерия согласия Пирсона проверить принадлежность эмпирического материала нормальной кривой распределения (кривая Гаусса).

Как и при проверке однородности выдвигается нулевая гипотеза, но в данном случае она утверждает согласие значений выборки со значениями нормальной кривой распределения, т. е. при увеличении данных натурных наблюдений до бесконечности, распределение случайных чисел отвечает выбранному закону распределения. Расчет по критерию Пирсона основан на определении теоретической частоты в эмпирических интервалах, и если эмпирическая частота и теоретическая отличаются незначительно, то принимается нулевая гипотеза при выбранном уровне значимости и числе степеней свободы. Расчетная формула статистического критерия согласия Пирсона или χ² имеет следующий вид:

(14)

где К — количество интервалов;

n_i — эмпирическая частота;

n_t — теоретическая частота.

Для того, чтобы использовать аналитические законы распределения, необходимо знать область возможных значений случайных величин (для нормально распределенной случайной величины область возможных значений определяется интервалом (-∞; +∞)).

Расчеты сводим в таблицу 4. При этом необходимо выполнить следующее условие: для граничных классов N⋅Pi > 1, а для внутренних — N⋅Pi > 5. Если условие не соблюдается, то классы необходимо укрупнять.

Таблица 4

Определение выборочного значения χ² на согласие эмпирического распределения с нормальным законом распределения.

№	ai	ni	bi		Ф0(bi)		Pi	N·Pi	ni -N·Pi	χ2рас(i)
1	2	3	4		5		6	7	8	9
0 1 2 3 4 5 6 7	-∞ - 18,3 18,3 – 19,57 19,57 – 20,84 20,84 – 22,11 22,11 – 23,38 23,38 – 24,65 24,65 – 25,92 25,92 - +∞	0 6 6 6 5 4 3 0	-∞ -1,64 -1,01 -0,39 0,26 0,85 1,47 2,09	- 1,64 -1,01 -0,39 0,26 0,85 1,47 2.09 +∞	-0,5 -0,45 -0,34 -0,15 0,003 0,2 0,43 0,48	-0,4 -0,34 -0,15 0,003 0,2 0,43 0,48 0,5	0,05 0,11 0,19 0,15 0,2 0,23 0,05 0,02	1,5 3,3 5,7 4,5 6 6,9 1,5 0,6	-1,5 2,7 0,3 1,5 -1 -2,9 1,5 -0,54	1,5 2,2 0,02 0,5 0,17 1,22 1,5 0,49
					∑		1,00	30		7,59

Условные обозначения:

a_i — границы интервалов;

n_i — эмпирическая частота;

b_i — нормированная и центрированная случайная величина:

(15)

Ф_о(b_i) — значение функции нормального закона распределения на границах интервалов определяется по таблицам;

P_i — теоретическая вероятность попадания случайной величины в заданный интервал,

P_i = Ф_о(b_i) - Ф_о(b_i-1);

N — объем выборки, N = 30;

N⋅P_i — теоретическая частота.

Критическое значение критерия Пирсона определяется по таблицам или по формуле:

(16)

где m — число степеней свободы, m = K – 1;

Z_2α — коэффициент, определяемый по формуле:

2 ⋅Ф (Z_2α) =1− 2α; Ф (Z_2α) = 0,45; Z_2α=1,65

Учитывая это, критическое значение критерия Пирсона равно:

Критическое значение критерия Пирсона можно определить по таблицам χ² - распределения в Приложении 3 методических указаний.

Если расчетное значение не превышает критического на выбранном уровне значимости, нулевая гипотеза принимается, что подтверждает принадлежность исследуемой выборки нормальному закону распределения.

Вывод: χ²_кр > χ²_рас>H₀

Эмпирическое распределение согласуется с кривой Гаусса. Все свойства с данной кривой Гаусса мы можем использовать для прогнозирования, моделирования и управления.

Заключение

Условие соблюдается: критическое значение распределения Пирсона больше расчетного (7,59<10,81), значит, нулевая гипотеза применяется, эмпирическое распределение согласуется с кривой Гаусса, можно применять все свойства этой кривой и использовать при прогнозировании; выборка принадлежит нормальному закону распределения.

Мы построили вариационный ряд, сгруппировали данные, графически изобразили ряды, изучили форму кривой распределения, проверили статистические гипотезы. Результаты расчетов могут быть использованы в дальнейших исследованиях, в частности, для математического моделирования трансформации загрязняющего вещества в водной и воздушной средах.