3.2 Меры рассеивания:

Характеристикой рассеивания или отклонения случайной величины от центра распределения выступает дисперсия – второй центральный момент.

Согласно методу моментов дисперсия определяется по формуле:

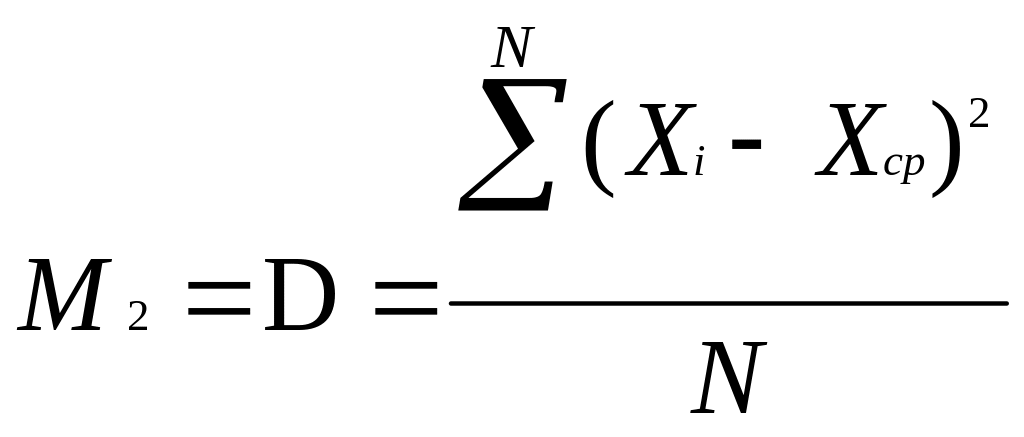(мг/л)² (8)

L=2,3,4

Определение центральных выборочных моментов

K	ni	Zi	Zi2	Zi3	Zi4	ni ∙Zi2	ni ∙Zi3	ni ∙Zi4
1	2	3	4	5	6	7	8	9
1 2 3 4 5 6	6 6 6 5 4 3	-2,71 -1,44 -0,17 1,1 2,37 3,64	7,34 2,07 0,03 1,21 5,62 13,25	-19,9 -2,99 -0,01 1,33 13,31 48,23	53,94 4,31 0,001 1,46 31,55 175,55	44,04 12,42 0,18 5,5 22,48 39,75	-119,4 -17,94 -0,06 6,05 53,24 144,69	323,64 25,86 0,006 7,3 126,2 526,66
∑	30				∑	124,37	66,58	1009,67

Для определения стандартного отклонения из дисперсии извлекается квадратный корень, полученная величина называется средним квадратичным отклонением и обозначается

δ= √M₂ (мг/л). Нормированное отклонение определяется коэффициентом вариации:

(9)

M₂=(1/30)∙124,37=4,15 δ= 2,04 С_v=0,094

3.3 Характеристики формы кривой распределения:

Характеристиками формы кривых распределения выступают третий и четвертый центральные моменты) третий центральный момент характеризует асимметричность ряда, т.е. неравномерность распределения случайной величины относительно центра и определяется по формуле:

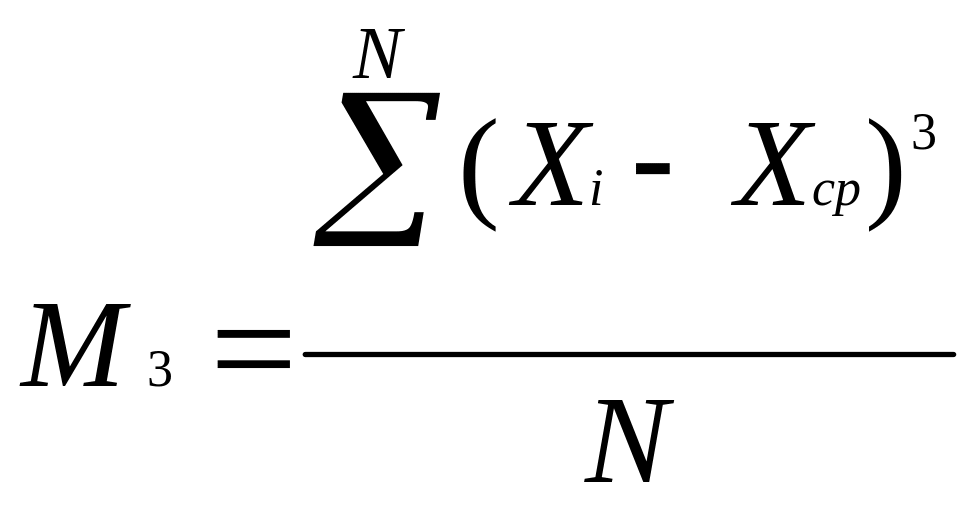(мг/л)³ (10)

M₃=2,22

Безразмерный коэффициент асимметрии (С_s) определяется отношением третьего центрального момента к кубу среднего квадратичного отклонения.

Четвертый центральный момент характеризует форму симметричной кривой распределения:

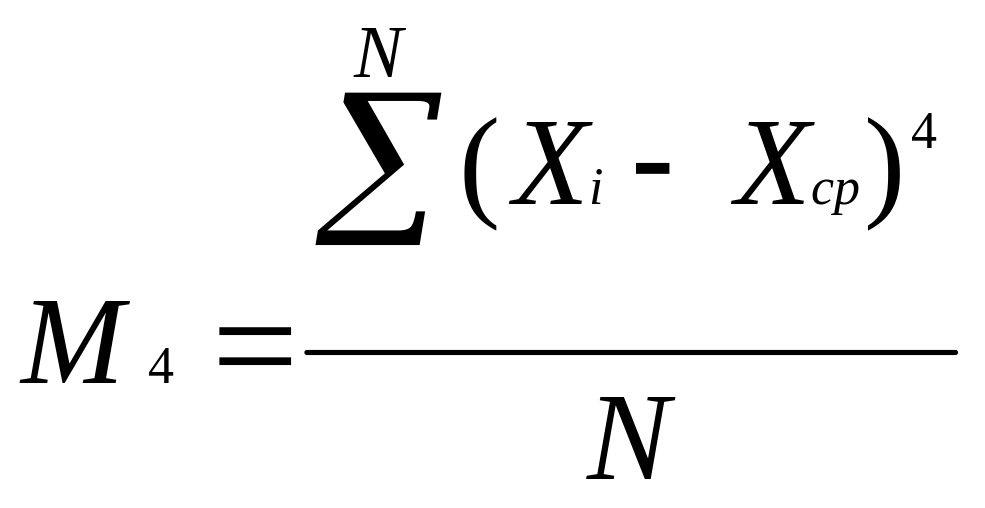(мг/л)⁴ M₄=33,66 (11)

Показателем остро- или плосковершинности выступает коэффициент эксцесса (С_е), который определяется отношением четвертого центрального момента к среднему квадратичному отклонению в четвертой степени, за вычетом коэффициента три.

4. Графическое изображение вариационных рядов.

Для графического изображения рядов распределения применяют гистограмму (кривая распределения плотности вероятностей, дифференциальная кривая распределения).

С помощью гистограммы (кривая распределения плотности вероятностей, дифференциальная кривая распределения) эмпирического распределения можно предугадать вид генеральной совокупности (случайной величины, подчиняющейся определенной функциональной зависимости).

Определение ординат эмпирических кривых распределений заносим в таблицу 3.

Таблица 3

	Границы интервалов мг/л	Частота ni	Относительная частота nотн	Приведенная частота nпр
1	2	3	4	5
1 2 3 4 5 6	18,3 - 19,57 19,57 -20,84 20,84 - 22,11 22,11 - 23,38 23,38 - 24,65 24,65 - 25,92	6 6 6 5 4 3	0,2 0,2 0,2 0,17 0,13 0,1	0,16 0,16 0,16 0,13 0,10 0,08

n_отн — относительная частота определяется отношением эмпирической частоты к объему выборки и характеризует вероятность появления случайной величины в каждом интервале.

n_пр — приведенная частота или плотность распределения случайной величины в заданном интервале

Гистограмма

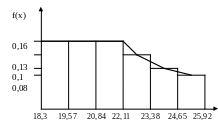
25

35 30

5