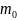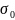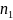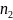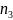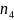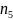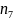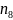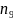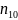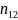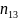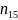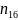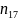Выборка №3.
Исходные данные:
|
50 |
|
15 |
a |
7,5 |
b |
92,5 |
h |
5 |
число интервалов |
17 |
|
6 |
|
9 |
|
14 |
|
36 |
|
46 |
|
86 |
|
104 |
|
127 |
|
136 |
|
125 |
|
106 |
|
81 |
|
51 |
|
32 |
|
16 |
|
8 |
|
5 |
В данной выборке рассматривается случай непрерывной случайной величины. Мы будем работать со случайной величиной, имеющей нормальное распределение, что позволит нам, познакомится с характеристическими свойствами этого распределения. На этом примере мы познакомимся с приемами работы с большими выборками, а именно с линейным преобразованием исходных данных.
a=7,
5 – начало первого интервала; b=92,5
– конец последнего интервала; h=5
– интервальный шаг; N=17
– число интервалов; N=988
– объем выборки;
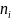 – данные заранее частоты;
– данные заранее частоты;
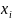 – середины интервалов.
– середины интервалов.
Сведем все наши расчеты в Таблицу 7.
Визуализация данных.
Построим гистограмму:
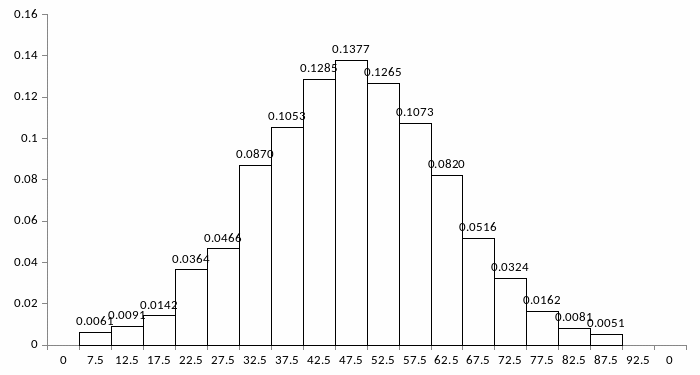
Построим график эмпирической функции распределения:
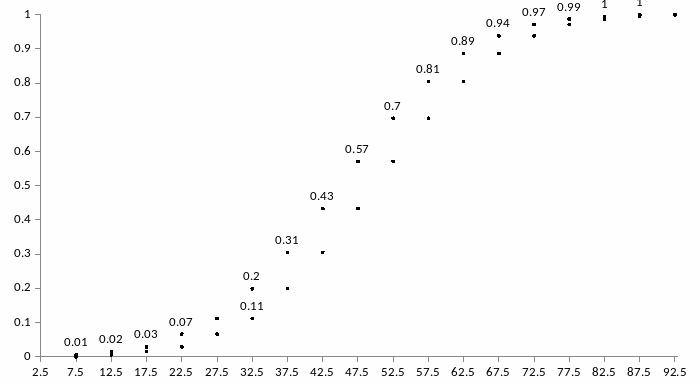



Теперь строим кривую Кетли:
Замена переменных в статистике.
Пользуясь
вычислительными теоремами выборочной
теории, осуществим переход от
к
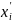 по формуле:
по формуле:
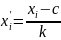 .
.
В качестве c берем середину серединного интервала, таким образом, c=50. В качестве k возьмем k=8.
Произведем
расчет
 ,
,
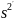 ,
,
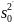 ,
,
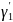 ,
,
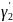 .
.
Восстановление подлинных значений этих величин:
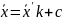 ;
;
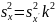 ;
;
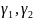 те же самые что и
,
.
те же самые что и
,
.
Из
таблицы 7 получаем
=
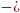 0,0101;
0,0101;
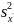 =
3,35;
=
3,35;
Восстанавливаем выборочное среднее для исходных данных:
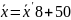 =
-0,010*8+50=49,92;
=
-0,010*8+50=49,92;
Восстанавливаем выборочную дисперсию для исходных данных:
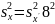 =3,35*64=214,16;
=3,35*64=214,16;
 =
=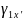 =
=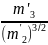 =
0,013;
=
0,013;
 =
= =
=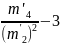 =
0,115;
=
0,115;
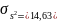 ;
;
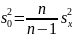 =
214,38;
=
214,38;
Выводы:
в среднем изучаемая случайная величина
принимает значение 49,92 и колеблется в
пределах 49,92
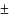 14,63.
Коэффициенты эксцесса и асимметрии
близки к нулю. Это значит, что распределение
вероятностей симметрично относительно
средней выборочной; так как коэффициент
эксцесса примерно равен нулю, то возможно
мы имеем нормальное распределение
вероятностей.
14,63.
Коэффициенты эксцесса и асимметрии
близки к нулю. Это значит, что распределение
вероятностей симметрично относительно
средней выборочной; так как коэффициент
эксцесса примерно равен нулю, то возможно
мы имеем нормальное распределение
вероятностей.
Расчет моды.
Найдем модальный интервал. Для этого в таблице 7 выберем интервал с наибольшей частотой. Модальный интервал (47,5; 52,5).
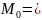 47,5-5
47,5-5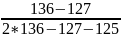 = 49,5
= 49,5
Вывод: мода равна 49,5. Около этого числа концентрируются те значения случайной величины, которые принимаются чаще всего.
Вычисление выборочной медианы.
Ищем сначала медианный интервал, пользуясь рассчитанными в таблице 7 накопленными относительными частотами.
 = 0,433 < 0,5 8-я строка
таблицы 7;
= 0,433 < 0,5 8-я строка
таблицы 7;
= 0, 697 > 0,5 10-я строка таблицы 7.
Вывод: накопленная относительная частота равная 0,5 достигается на 9-ом интервале.
Медианный интервал (47,5; 52,5).
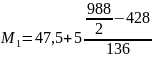 = 49, 93;
= 49, 93;
Вывод: медиана равна 49, 93.


 50%
50%
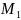 50%
50%
49, 93
делит числовую ось на две равновероятные области событий: 50% принимаемых значений меньше 129,99 и 50% больше.
Обратим внимание на ряд особенностей, возникших при расчете данной выборки:
1). Модальный и медианный интервалы совпали, этой особенностью обладает нормальное распределение вероятностей;
2).
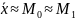
 50
– это тоже характерно для нормального
распределения;
50
– это тоже характерно для нормального
распределения;
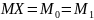 ;
;
3).
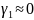 ,
,
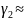 0 - отражает свойства нормального
распределения вероятностей:
0 - отражает свойства нормального
распределения вероятностей:
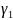 =
= в
в
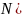 ).
).