2. Теплоотдача при свободном движении в гравитационном поле

При взаимодействии жидкости с холодной или горячей стенкой её плотность изменяется. Из-за этого возникает свободное движение (свободная конвекция) жидкости. В гравитационном поле нагретые объёмы жидкости поднимаются вверх, а охлаждённые – опускаются вниз.

Характер движения жидкости около стенки зависит от формы поверхности, её положения в пространстве и направления теплового потока. Это хорошо видно из рисунка 2.1. В нижней части охлаждаемой вертикальной стенки (см. рисунок 2.1а) движение жидкости происходит в ламинарном пограничном слое. После небольшого переходного участка жидкость движется в турбулентном пограничном слое. Если вертикальная стенка нагреваемая, то жидкость течет сверху вниз в той же последовательности. С увеличением температурного напора сокращается длина ламинарного пограничного слоя и увеличивается протяжённость турбулентного пограничного слоя. В пределах ламинарного течения коэффициент теплоотдачи уменьшается с увеличением толщины ламинарного пограничного слоя, в переходной области – увеличивается. В пределах турбулентного пограничного слоя коэффициент теплоотдачи практически не изменяется.

Теплоотдача около плоских горизонтальных поверхностей зависит от их расположения и направления теплового потока. В схемах 2.1в и 2.1г горизонтальная стенка стесняет движение жидкости. В этих случаях теплообмен происходит менее интенсивно, чем в случаях, изображённых на рисунках 2.1б и 2.1д.

Михеев М.А. установил, что форма и расположение поверхностей стенок при свободной конвекции незначительно влияют на тепоотдачу. Поэтому им было предложено единое уравнение подобия для тел различной конфигурации. В качестве определяющего числа подобия использовано число Рэлея .

Для определения средних значений безразмерных коэффициентов теплоотдачи тел с различной формой поверхности в неограниченном пространстве Михеев М.А. предложил формулу:

. (2.12)

Значения величин с и n в уравнении (2.12) зависят от числа Рэлея и приведены в таблице 2.1.

Таблица 2.1

Ram	10-35·102	5·1022·107	2·1071013
c	1,18	0,54	0,135
n	1/8	1/4	1/3

В формуле (2.12) за определяющую температуру принята средняя температура пограничного слоя . Выбор определяющего размера зависит от формы и расположения поверхности теплообмена. Для труб и шаров за определяющий размер следует выбирать их диаметр. Для вертикальных стенок – их высоту, для горизонтальных плоских поверхностей – наименьший горизонтальный размер.

Значение коэффициента теплотдачи, полученное по формуле (2.12) для горизонтальных плоских поверхностей, показанных на рисунках 2.1б и 2.1д, необходимо увеличить на 30%, а для схем на рисунках 2.1в и 2.1г – уменьшить на 30%.

Значения числа , приведенные в таблице 2.1, разбиты на три диапазона, соответствующие трём различным режимам теплообмена. При =10^-35·10² имеет место режим псевдотеплопроводности, при котором движение жидкости практически не отражается на переносе теплоты. При =5·10²2·10⁷ течение носит ламинарный, а при =2·10⁷10¹³ – турбулентный характер.

Характер свободного движения жидкости в ограниченном пространстве зависит от формы и взаимного расположения поверхностей, образующих прослойку, а также от расстояния между ними. При теплоотдаче в замкнутом пространстве, показанном на рисунке 2.2, перенос теплоты осуществляется одной и той же жидкостью. Она циркулирует между горячей и холодной стенками, образуя замкнутые контуры. В этом случае трудно отделить 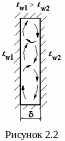теплоотдачу около охлаждаемой и нагреваемой поверхностей. Поэтому процесс теплообмена в замкнутой прослойке оценивают в целом, определяя плотность теплового потока по формуле теплопроводности:

, (2.13)

где - эквивалентная теплопроводность; - толщина прослойки.

Эквивалентная теплопроводность учитывает интенсивность циркуляции в прослойке и определяется через теплопроводность жидкости по формуле:

, (2.14)

где - коэффициент конвекции.

Эксперименты показывают, что независимо от формы прослойки коэффициент конвекции можно определять по эмпирической зависимости:

. (2.15)

В формуле (2.15) величины c и n зависят от числа . Их значения приведены в таблице 2.2

Таблица 2.2

Ra f	103	103106	1061010
c	1,0	0,105	0,4
n	0	0,3	0,2

Из таблицы 2.2 видно, что при числах 10³ величина коэффициента конвекции =1. В этом случае в прослойке отсутствует циркуляция жидкости и теплота передаётся только теплопроводностью. Определение параметров, входящих в число , производится при определяющей температуре жидкости, равной . За определяющий размер принята толщина прослойки .