Модальное значение или мода.
Модой в статистике называется варианта, которая наиболее часто встречается в ряду распределения. Для дискретного ряда мода является характеристикой, которая определяется по частотам вариант и равна варианте, которая имеет наибольшую частоту.
В случае интервального ряда распределения первоначально находится интервал, содержащий модальное значение по такому же правилу, что и для дискретного ряда распределения, после чего абсолютное значение моды рассчитывается по следующей формуле:
-
нижняя граница модального интервала.
-
абсолютное значение модального интервала,
то есть разность между его верхней и
нижней границами.
-
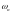частоты интервала, содержащего моду.
;
- частоты интервалов, соседних с модальным,
то есть соответственно предыдущего и
последующего интервалов.
Пример: На основании данных предыдущей таблицы рассчитать модальное значение урожайности зерновых культур:
Показатели вариаций.
Абсолютные.
–вариационный
размах, представляющий собой абсолютную
разность между максимальной и минимальной
вариантой;
и
-максимальное и минимальное значение
признаков в ряду распределения.
Среднее линейное отклонение -
,
представляет собой среднюю арифметическую
из абсолютных значений отклонений
вариантов от их средней арифметической
Дисперсия (
).
Данный показатель используется наиболее
часто в теории и на практике в качестве
меры колеблемости признака и представляет
собой среднюю квадратичную из отклонений
вариант от их средней арифметической.
И вычисляется, как дисперсия простая по формуле (3а) и взвешенная по (3б).
Средне квадратическое отклонение рассчитывается по формуле:
Показатели
имеют ту же размерность что и исходный
вариационный ряд и носят название
абсолютных показателей вариации.
В статистических исследованиях данные показатели дополняются относительными показателями вариации.
-
носит название коэффициент вариации
по вариационному размаху.
- носит
название коэффициент вариации по
среднему минимальному отклонению.
- носит
название коэффициент вариации по
среднему квадратичному отклонению.
Рассматренные коэффициенты (5а), (5б), (5в) могут быть вычислены и в дальнейшем выражены либо в долях единицы, либо в процентах.
Статистическое правило: если на то нет специальных указаний, все коэффициенты в статистике вычисляются с минимальной степенью точности равной трем знакам после запятой в долях единицы, если же в процентах, минимальная степень точности равна одному знаку после запятой.
В практике цивилизованных стран минимально соответственно 4 и 2 знака после запятой.
Статистическое правило: степень точности, расчетных данных не должна превышать степень точности исходных данных, если на то нет специальных указаний.
Порядок расчета дисперсии взвешенной.
Находится средняя арифметическая методом моментов, или как взвешенная.
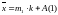
Находятся отклонения каждой варианты от их средней арифметической, то есть находятся разности вида:
Полученные отклонения вариант от их средней арифметической возводим в квадрат:
Находим произведения квадратов отклонений от их средней арифметической на частоты или частости:
Находим сумму произведений полученных в пункте 4, то есть сумму квадратов отклонений вариант от их средней арифметической, умноженную на соответствующие частоты (или частости)
Определим сумму частот или частостей, то есть численность совокупности:
Рассчитаем дисперсию:
