11.График зависимости координаты (перемещения) от времени в равноускоренном движении.
Р
ассмотрим
наиболее простой случай (
,
тогда
.
Квадратичная зависимость координаты от времени изображается графиком параболы Рис.22
В равнозамедленном
движении, при
график есть парабола, ветви которой
направлены вниз Рис.23
П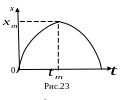
ри
координата достигает максимума
,
тело делает остановку и начинает
двигаться в противоположном направлении.
При этом время движения от
до
равно времени движения в обратном
направлении от
до
ввиду симметрии параболы.
12. Свободное
падение тел
– ускоренное движение тел под действием
силы притяжения Земли в безвоздушном
пространстве. Все тела независимо от
их массы в безвоздушном пространстве
падают с одинаковым ускорением, называемым
ускорением свободного падения. Вблизи
поверхности Земли ускорение свободного
падения равно
.
При падении тел в воздухе действует сила сопротивления воздуха, которая увеличивается по мере возрастания скорости. В первые моменты тело падает с ускорением, но когда сила сопротивления становится равной силе притяжения тела к Земле, оно продолжает падать равномерно.
Чем тяжелее тело, тем большую скорость оно успеет получить за время, в течение которого сила сопротивления воздуха уравновесит силу притяжения тела к Земле.
При свободном падении тела путь, пройденный телом и его скорость вычисляются по формулам для равноускоренного прямолинейного движения, в котором роль ускорения играет ускорение свободного падения g.
Направим ось У вниз, тогда закон движения в свободном падении запишнтся в виде
.
Если
то
.
Если тело брошено вертикально вверх с начальной скоростью , то g<0 поэтому уравнение движения записывается в виде:
Из последнего равенства следует, что график зависимости координаты у от времени для тела, брошенного вертикально вверх есть парабола, ветви которой направлены вниз, Рис.23,
Из симметрии параболы следует, что время в течении которого время тело достигнет максимальной высоты, равно времени падения тела а этой высоты.
На максимальной высоте скорость тела равна нулю следовательно
Поэтому время
,
в течении которого тело достигнет
максимальной высоты
равно
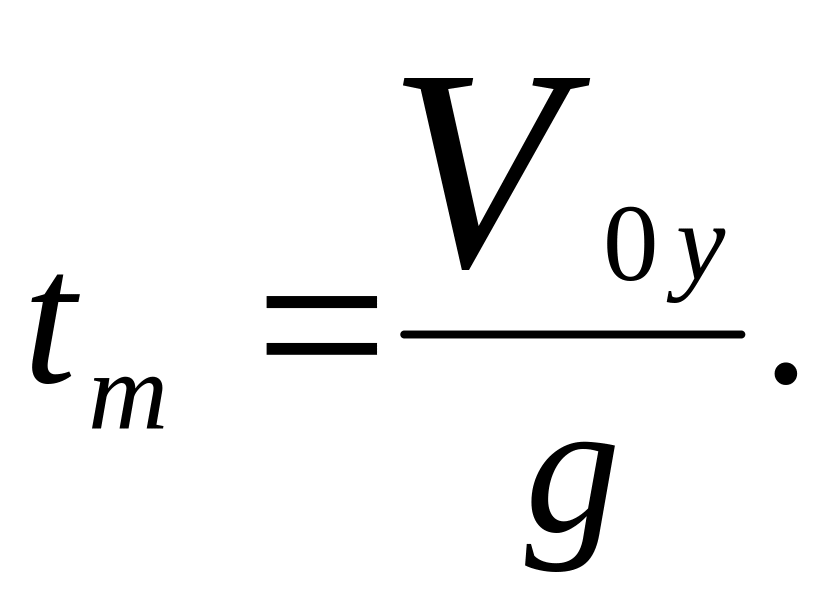
Подставляя в уравнение параболы получим выражение для вычисления максимальной высоты
.
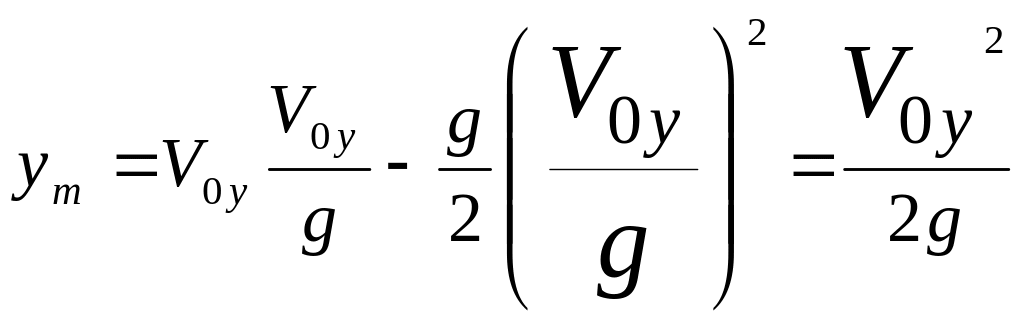Итак, максимальная
высота, на которую может подняться
тело, брошенное вертикально вверх с
начальной скоростью
равна
.
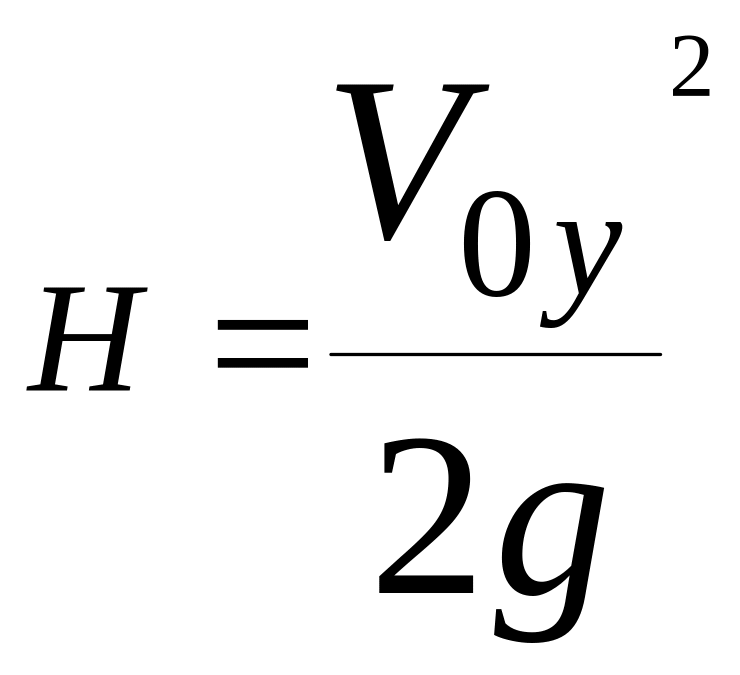1
3.Движение
тела, брошенного под углом к горизонту.
Пусть тело начинает двигаться с начальной
скоростью
,
направленной под углом
к горизонту и пусть движение начинается
из начала координат, ось
которой направлена горизонтально , а
ось у вертикально вверх Рис.24.
Разложим скорость
на две составляющие
=
горизонтальная
и
=
-
вертикальная составляющие Рис.24
В горизонтальном направлении тело движется равномерно со скоростью . По вертикали первую половину всего времени движения тело движется равнозамедленно вверх с ускорением ( -g) и начальной скоростью , вторую половину времени – равноускоренно вниз с ускорением g.
Можно сказать, что тело участвует в двух независимых друг от друга движениях согласно уравнениям:
.
y=
.
Исключая время получим уравнение траектории движения тела брошенного под углом к горизонту (траектории баллистического движения)
,
,
Сокращая на
и учитывая, что
получаем уравнение траектории
.
Таким образом, мы получили, что траектория тела, брошенного под углом к горизонту, есть парабола, ветви которой направлены вниз (Рис.24) .
Максимальную высоту полета найдем так же как максимальную высоту тела, брошенного вертикально вверх со скоростью =
.
Дальность полета равна расстоянию между точками, в которых парабола пересекает ось Х , т.е. точками, в которых у=0. Эти значения х мы получим, решая квадратное уравнение
,
.
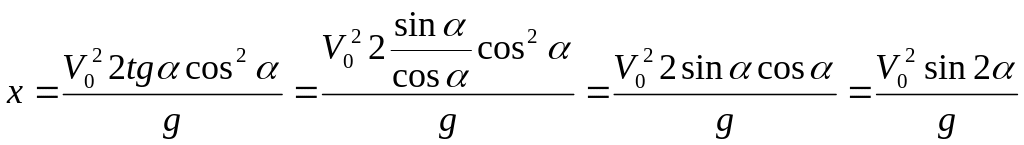Движение началось из точки , поэтому дальность полёта S равна x , т.е.
S=
.
