76

Лекция – 1. Кинематика. Часть – 1. 2

Лекция – 2. Кинематика. Часть – 2. 7

Лекция – 3. Кинематика. Часть – 3. 14

Лекция- 4. Динамика. 18

Лекция – 5. Силы гравитации. 22

Лекция – 6 . Сила упругости. Сила трения. 25

Лекция – 7. 31

Лекция – 8. Импульс. Закон сохранения импульса 34

Лекция – 9. Работа и энергия. 38

Лекция – 10. Статика. 43

Лекция – 11. Гидроаэростатика. 47

Лекция – 12. Гидроаэродинамика. 53

Лекция – 13. Механические колебания. 58

Лекция – 14. Механические волны. 67

Лекция – 1. Кинематика. Часть – 1.

1. Механическое движение

2. Поступательное движение

3. Вращательное движение

4. Классическая физика

5. Материальная точка

6. Система отсчёта

7. Принцип дальнодействия

8. Кинематика

9. Траектория точки

10. Перемещение

11. Путь

12. Средняя путевая скорость

13. Мгновенная скорость

14. Средняя по перемещению скорость

15. Вектор мгновенной скорости

16. Сложение скоростей

17. Относительная скорость

18. Прямолинейное равномерное движение

19. График прямолинейного равномерного движения

20. График скорости равномерного движения.

1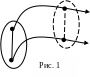 .Механическое движение – это изменение положении тела в пространстве относительно других тел с течением времени, либо изменение положения одной части тела относительно других его частей.

2 .Поступательное движение – это такое движение, при котором отрезок прямой, соединяющий две какие-либо точки тела, остается параллельным самому себе Рис.1. Иными словами при поступательном движении все точки тела описывают одинаковые

траектории.

3.Вращательное движение – это движение, при котором неподвижными остаются точки тела, лежащие на некоторой прямой, называемой осью вращения. Траектории точек тела не лежащих на оси есть окружности, плоскости которых перпендикулярны оси, а их центры лежат на этой оси Рис. 2

4.Классическая физика изучает движения тел, происходящие со скоростью много меньшей скорости света С=300000 , ( <<C). Это значит, что скорость света в классической физике принимается бесконечно большой.

5.Материальная точка – это тело, обладающее массой, размерами которого в условиях данной задачи можно пренебречь.

Примеры:

а) При поступательном движении тела все его точки описывают одинаковые траектории и движутся с одинаковыми скоростями и ускорениями. Поэтому достаточно изучать движение одной какой- либо его точки, например центра масс.

б) Определяя период обращения планеты вокруг Солнца, планету можно считать материальной точкой.

в)Работа при подъёме тела массы m высоту h вычисляется по формуле А= mgh, здесь h – высота, на которую поднимается центр масс тела. В этом случае тело можно считать материальной точкой.

6.Система отсчета. Характер движения тела (траектория, скорость, ускорение) зависит от выбора тела (тела отсчёта), относительно которого изучается это движение. Например, пассажир, сидящий в движущемся трамвае, относительно трамвая находится в покое, а относительно улицы движется.

Д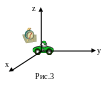 ля того чтобы точно охарактеризовать движение необходимо в каждый момент времени знать координаты, скорость и ускорение материальной точки. Для этого используется система отсчёта.

Система отсчёта – это тело отсчёта, жестко связанная с ним система координат и часы, расположенные в начале координат, На которых указано начало отсчёта времени Рис.3

7 . Принцип дальнодействия. Скорость передачи информации в классической физике принимается бесконечно большой, т.е. информация из любой точки пространства мгновенно достигает начала координат. Поэтому достаточно иметь только одни часы, расположенные в начале координат. В этом и состоит смысл принципа дальнодействия.

8.Кинематика есть раздел физики, изучающий движение тел, без учёта причин (сил), вызывающих изменение этого движения.

9.Траектория точки – линия, которую описывает материальная точка при своем движении относительно данной системы отсчёта на Рис.4 кривая, проведённая из начального положения 1 в конечное положение 2.

10.Перемещение – вектор, проведённый из начального положения 1 материальной точки в конечное её положение 2. На Рис.4 - перемещение. В системе СИ модуль перемещения измеряется в метрах.

В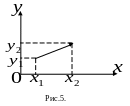 ектор перемещения можно спроектировать на оси координат и получить его проекции: - , - Рис.5

11.Путь – длина участка траектории, пройденного точкой за данный интервал времени. В системе СИ путь скалярная величина, измеряемая в метрах. На Рис.4 путь обозначен буквой S.

12. Средняя путевая скорость – скалярная физическая величина, равная отношению пути S к интервалу времени t, затраченному на его прохождение;

= ,

В системе СИ скорость измеряется в метрах на секунду .

13.Мгновенная скорость – средняя скорость за бесконечно малый промежуток времени, т.е. предел, к которому стремится отношение при условии, что t стремится к нулю ( t 0). Это записывается в виде .

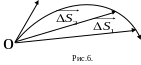14. Средняя по перемещению скорость – отношение перемещения точки к интервалу времени, в течении которого оно произошло: = .

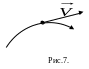15.Вектор мгновенной скорости. Пусть точка движется по кривой Рис. 6. Движение начнем изучать от точки 0. При уменьшении интервала времени вектор перемещения уменьшается по модулю, а его направление становится всё ближе к прямой касательной к траектории в точке 0. При 0 вектор перемещения совпадет с касательной к траектории и точке 0. Из этого следует, что в каждый момент движения вектор скорости (вектор мгновенной скорости) направлен по касательной к траектории в сторону движения Рис.7.

16.Сложение скоростей. Пусть по реке плывёт плот, а по плоту перемещается человек. Положим, что течение реки направлено по оси , по плоту человек перемещается вдоль оси y. За время плот переместился , а человек относительно плота – на . По правилу параллелограмма сложения векторов результирующее перемещение человека относительно берега равно диагонали параллелограмма , построенного на векторах и Рис.8:

+ .

Поделив обе части этого равенства на получим

= + .

Учитывая, что = , = - скорости человека относительно плота и плота относительно берега соответственно, а = скорость человека относительно берега запишем = + .

Итак, результирующая скорость – скорость человека относительно берега равна диагонали прямоугольника, построенного на векторах и Рис. 8. Это же правило справедливо при любых углах между компонентами и Рис.9

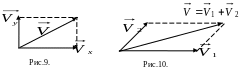
Если и параллельны и их направления совпадают, т.е. , то модуль результирующей скорости равен алгебраической сумме модулей компонент + , а её направление совпадает с направлением и . Если же скорости и противонаправлены – антипараллельны , то модуль результирующей скорости равен модулю алгебраической разности модулей компонент - , а её направление совпадает с направлением большей по модулю компоненты.

17.Относительная скорость. Пусть два автомобиля движутся относительно по щоссе со скоростями и , тогда скорость одного из них относительно другого называется относительной скоростью. Если автомобили сближаются или удаляются друг от друга, то относительная скорость равна сумме их скоростей: + . При движении в одном направлении модуль относительной скорости модулю разности их скоростей - . При этом, если автомобиль скорость которого меньше движется вслед за автомобилем, скорость которого больше они удаляются друг от друга, если же наоборот, то они сближаются.

18.Прямолинейное равномерное движение – движение с постоянной по модулю и направлению скоростью = . Это движение удобно рассматривать, вдоль оси х. Тогда перемещение можно рассчитать по формуле t, где , - положение точки на оси х в момент времени t = 0, х - положение точки в момент времени t . Учитывая, что Рис.11 получим = t и далее

t + .

П оследнее равенство есть уравнение прямолинейного равномерного движения. Оно показывает зависимость координаты х от времени. Если при t=0 точка находилась в начале отсчета, т.е. = 0, то уравнение движения принимает вид

t.

19.График равномерного прямолинейного движения. Откладывая на оси ординат координату х , а на оси абсцисс время t получим график прямолинейного равномерного движения для случаев = 0, Рис.12. Графиком прямолинейного равномерного движения, т.е. функции х(t) является прямая линия Рис. 12.

Угол наклона графика к оси времени зависит от скорости: > , > Рис.13.

С остояние покоя ( =0) изображается прямой параллельной оси времени, т.к. х(t) = 0 Рис.14

20.График равномерного движения. Если на оси ординат откладывать скорость, а на оси абсцисс время, то график прямолинейного равномерного движения или просто равномерного движения изобразится прямой линией параллельной оси времени = const или const Рис.15.

П уть пройденный в равномерном движении рассчитывается по формуле S=V t. На графике скорости путь, пройденный за время равен площади фигуры ограниченной графиком скорости и осью времени, т.е. площади прямоугольника со сторонами и Рис.16.