Содержание.
Условные обозначения.
Выражения и преобразования.
Решение простейших уравнений и неравенств: квадратных, рациональных (дробно-рациональных).
Понятие модуля. Решение простейших уравнений и неравенств с неизвестным под знаком модуля.
Понятие логарифма, свойства логарифмов, логарифмические преобразования. Логарифмирование и потенцирование. Показательная и логарифмическая функции. Простейшие показательные и логарифмические уравнения и неравенства.
Тригонометрические преобразования. Таблицы значений основных тригонометрических функций. Обратные тригонометрические функции. Решение простейших тригонометрических уравнений.
Декартова система координат. Построение точек и прямых. Понятие функции. Свойства функций. Графики элементарных функций.
Производная (правила дифференцирования, таблица производных, сложная производная).
Задачи для подготовки к итоговому тесту.
Итоговый тест.
1. Условные обозначения.
- множество всех натуральных чисел.
- множество всех целых чисел.
- множество всех рациональных чисел.
- множество всех действительных
(вещественных) чисел.
- множество всех положительных
действительных чисел.
- следует.
- равносильно; эквивалентно; тогда и
только тогда.
- по определению равно.
- область определения функции
.
- множество (область) значений функции
.
- постоянная величина.
- принадлежит, содержится (например,
-
принадлежит множеству
действительных чисел, то есть является действительным числом).
2. Выражения и преобразования.
Определения степени и корня.
Пусть
,
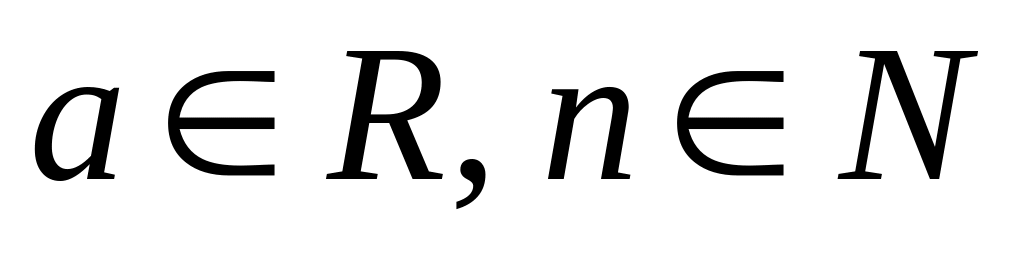тогда:
;
если
;
если
;
не определено;
и
при
четном;
при нечетном.
Пусть , тогда:
.
Правила действия с радикалами.
Пусть
тогда:
|
|
|
|
|
|
Правила действия со степенями.
Пусть
,
тогда:
|
|
|
|
Замечание: приведенные правила
действия верны и для
.
Формулы сокращенного умножения.
Пусть
,
тогда:
;
;
;
;
.
Пример. Вычислить.
1)
.
2)
.
3)
.
4)
.
5)
6)
=0,6
7)
.
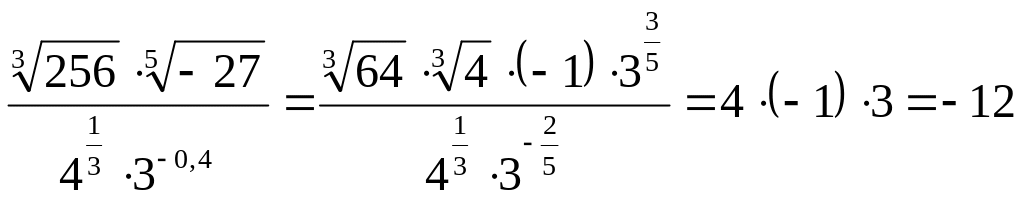8)
.
9)
.
10)
.
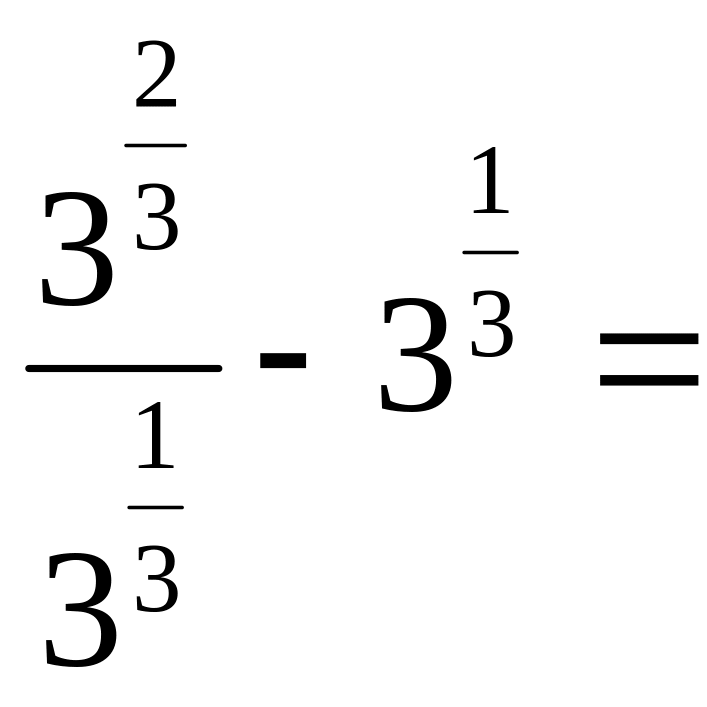
Пример. Вычислить.
1)
=
2)
=
.
3)
.
4)
.
Пример. 1. Найти значение
выражения
,
если
.
2. Найти значение
выражения
,
если
.
Решение: 1.
={при
}=
.
Ответ: 1) 9; 2) -8.
Пример. Найти значение выражения.
1.
,
при
.
2.
,
при
.
3.
,
при
.
Решение: 1. Вычислим сначала значение подкоренного выражения.
,
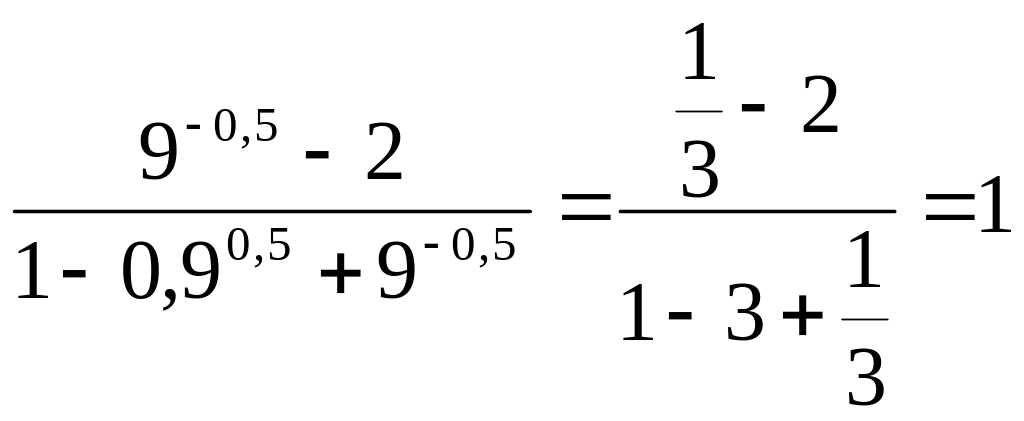тогда
.
2.
3.
при
,
получаем 3.
Ответ: 1) 1; 2) 3; 3) 3.
Пример. Вычислить значение выражения.
1.
.
2.
.
3.
.
Решение: 1. Представим оба подкоренных выражения в виде полных квадратов:
и
,
тогда
.
2.
=
.
3.
.
Ответ: 1) -3; 2) 4; 3) 3.
Пример. Представьте выражение
в виде многочлена стандартного
вида.
Решение:
=
.
Пример. Разложите многочлен
на
множители.
Решение:
.
Пример. Упростите выражение
.
Решение:
=
.
Пример. Упростите выражение
Решение: Проведем преобразования
в ОДЗ (
).
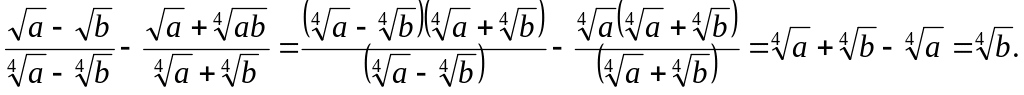
Пример. Упростите выражение
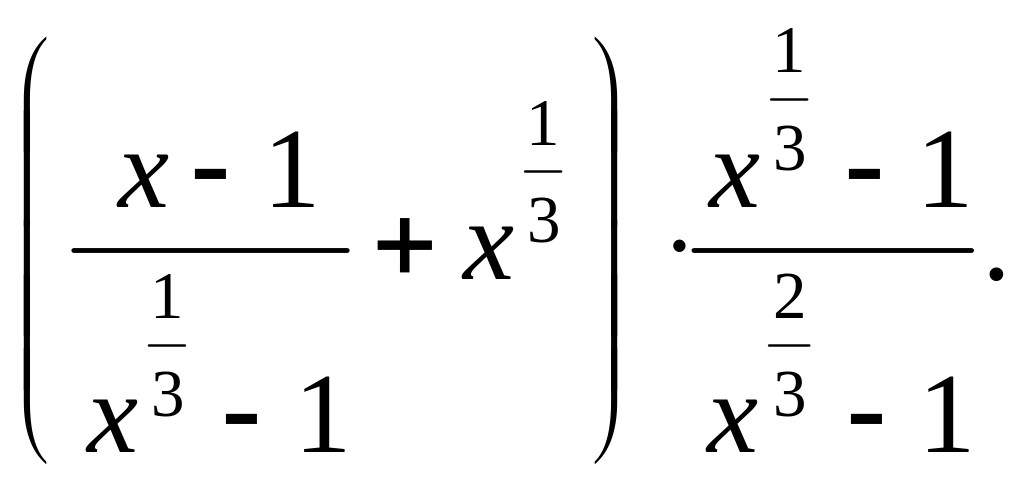
Решение: Проведем преобразования
в ОДЗ (
).
.
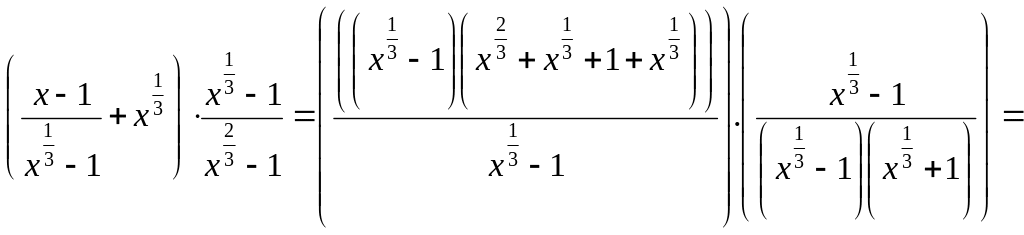
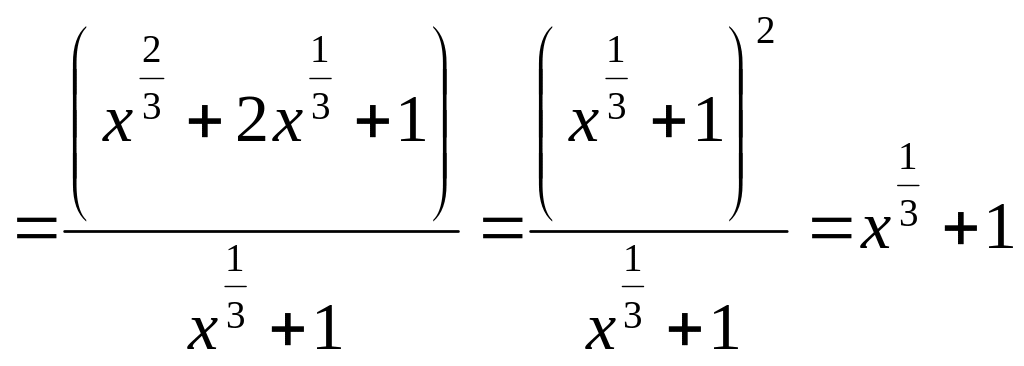Дополнительные задачи:
1. Упростить выражение:
а)
,
б)
.
Ответ: (на ОДЗ) а)
,
б)
.