Тема 1.2 Конвекційний теплообмін

Самостійна робота № 2 Основи теорії подібності. Теплове моделювання (2 год.)

Питання 1 Подібність в геометрії

Теорія подібності – це наука про подібні явища. Термін “подібність” взятий з геометрії. На-приклад, добре відомо, що для геометрично подібних фігур (нехай трикутників) відповідно кути

р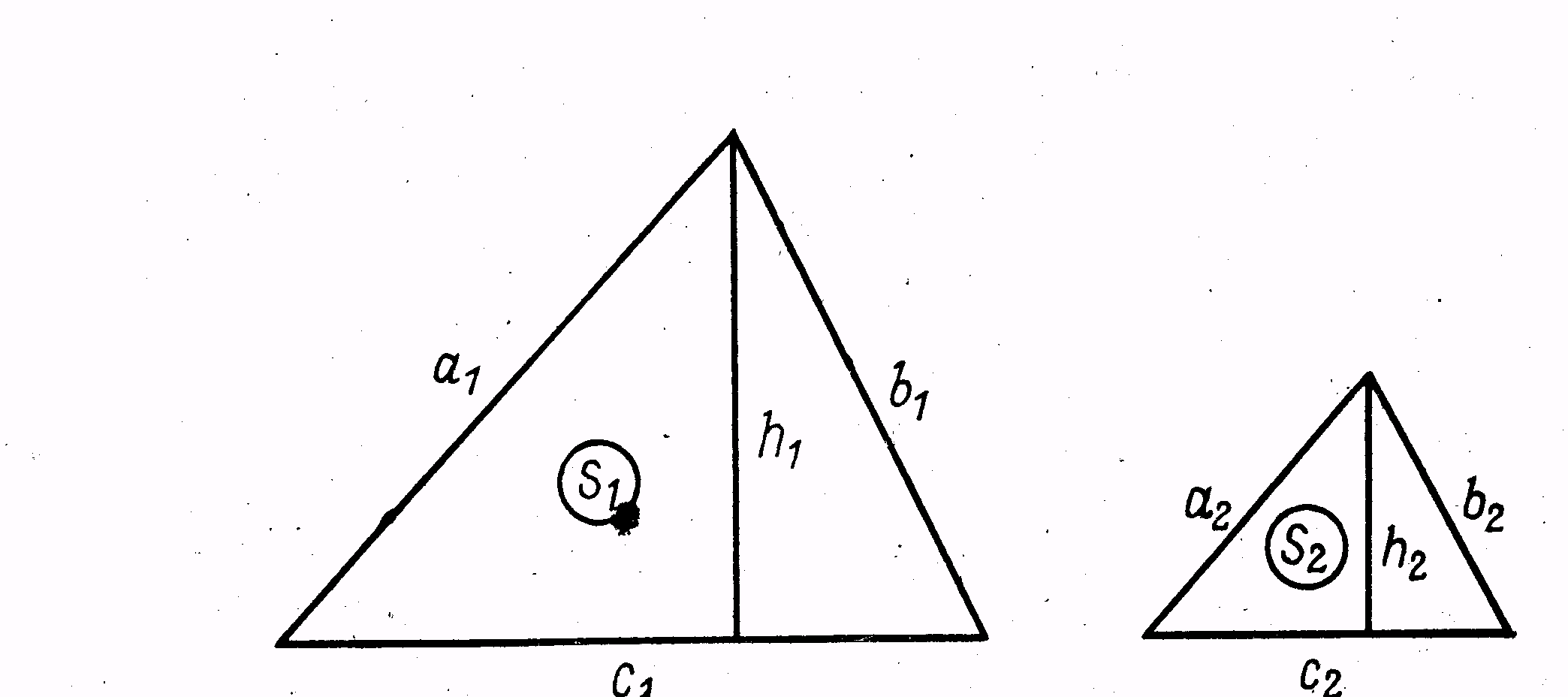 івні, а схожі боки пропорційні (рисунок 1.5).

Пропорційність лінійних розмірів потріб-но розуміти таким чином: будь - який лінійний розмір одного трикутника можна отримати, якщо взяти схожий лінійний розмір іншого, подібного йому трикутника і помножити його на деякий ко- ефіцієнт, що можна назвати коефіцієнтом подіб- ності

а₂=k_l а₁; h₂=k_l h₁. (1.9)

Рисунок 1.5 - Подібність плоских геометричних Якщо розглядати інший елемент подібних

фігур трикутників – їх площу, то в цьому випадку та-

кож існує зв’язок через коефіцієнт подібності. Але сам коефіцієнт має інше значення

S₂=k_s S₁. (1.10)

Зв’язок між коефіцієнтами k_l і k_s встановлюється на підставі зв’язку між самими елемента-ми, які порівнюються, одного й того ж трикутника. Площа трикутника пов’язана з основою і висо-

тою співвідношенням S=1/2 c h.

Звідси мають

S₁=1/2 c₁ h₁; S₂=1/2 c₂ h₂;

S₂/S₁= ; k_s= . (1.11,1.12)

Питання 2 Подібність фізичних явищ

Поняття подібність може бути поширено на будь-які фізичні явища. Воно може бути засто-совано до таких фізичних явищ, які якісно однакові й описуються однаковими аналітичними за-

лежностями як за формою, так і за змістом. Іначе кажучи, подібність двох фізичних явищ буде ли-ше в тому випадку, якщо буде дотримуватися подібність всіх величин, що характеризують ці яви-ща.

Два потоки рідини будуть подібні у тепловому відношенні, якщо вони обидва будуть обме- жені стінками геометрично подібної конфігурації і в потоках рідини будуть подібні між собою всі фізичні величини, тобто

w₂=k_w w₁; ₂=k_ ₁; ₂=k_ ₁. (1.13,1.14,1.15)

Коефіцієнти k_w, k_ , k_ називаються множниками перетворення подібності (або констан-тами подібності). Індекс, котрий ставиться у константи подібності, показує, до якої величини він відноситься. Ні від координат, ні від часу k не залежить.

При розгляданні складних процесів, які визначаються багатьма фізичними величинами, ви- бирати довільно константи подібності не можна. Для таких процесів під час вибору констант по- дібності існують обмеження, які знаходять шляхом дослідження рівнянь, які описують процес.

Розглянемо правило вибору констант подібності на конкретному прикладі рівняння тепло- провідності для одношарової плоскої стінки. Для неї . Нехай перша основна система ха- рактеризується значеннями параметрів q₁, ₁, , ₁, а друга – значеннями q_{2 =} k_q q₁, _{2 =} k_ ₁, , ₂ = k_l ₁. Значення параметрів другої системи отримані шляхом множення значень па-раметрів першої системи на відповідні константи подібності. Тоді для першої системи , а для другої . Поділивши перше рівняння на друге, отримують

або . (1.16)

Підставляючи замість відношення величин їх константи подібності, отримують

. (1.17)

Останнє рівняння показує, якою умовою обмежений вибір констант подібності для явища теплопровідності в двох подібних системах, що розглядаються. Виявляється, що константи подіб-ності k_q, k_l, k_, k_t необхідно вибирати таким чином, аби добутки k_q k_l і k_ k_t були б однакові.

Вимоги до вибору констант подібності, що обумовлені цим рівнянням, можна навести і в іншому більш зручному вигляді

або (1.18)

Рівняння (1.18) ілюструє основну властивість подібних між собою явищ, котра полягає в тому, що для всіх подібних між собою систем існують безрозмірні комплекси величин, які зберіга- ють одне й те ж чисельне значення. Ці комплекси носять назву інваріантів, що означає незмінні, або критеріїв (чисел) подібності. Критерії подібності прийнято позначати першими двома буква-ми прізвищ вчених, які багато зробили для розвитку відповідних галузей знань, наприклад

критерій Рейнольдса - відображає відношення сил інерції і сил в’язкості в

потоці рідини;

критерій Ейлера - характеризує подібність сил тиску;

критерій Пеклє - відображає співвідношення між конвективним тепло-

вим потоком і тепловим потоком теплопровідності;

критерій Прандтля - уявляє собою комплексну фізичну характеристику

властивостей речовини;

критерій Грасгофа ;

критерій Нусельта ;

критерій Фур’є та інші.

Критерій Нусельта, або критерій тепловіддачі, як той що містить у собі величину , є функ-цією критеріїв і тому для конвективного теплообміну критеріальне рівняння у самому загальному виді буде мати вигляд

Nu=f(Fo, Re, Gr, Pr).

Для практичних розрахунків критеріальні рівняння відображають у формі степеневих за- лежностей, наприклад

Nu_x=0,33 Re^0,5 Pr^0,33 або Nu_x=0,0296 Re^0,8 Pr^0,43 (Pr_ж/Pr_c). (1.19)

Роль критеріїв подібності особливо важлива. Для забезпечення подібності достатньо забез- печити подібність тільки критеріїв подібності – в даному випадку Re і Pr. В подібних процесах рівні не тільки числа Re і Pr, але й число Nu.

Для виконання самостійної роботи № 2 необхідно зробити конспект теоретичної частини.