§ 61. Взаимное расположение трех прямых

Пусть относительно общей декартовой системы координат заданы общие уравнения трех прямых:

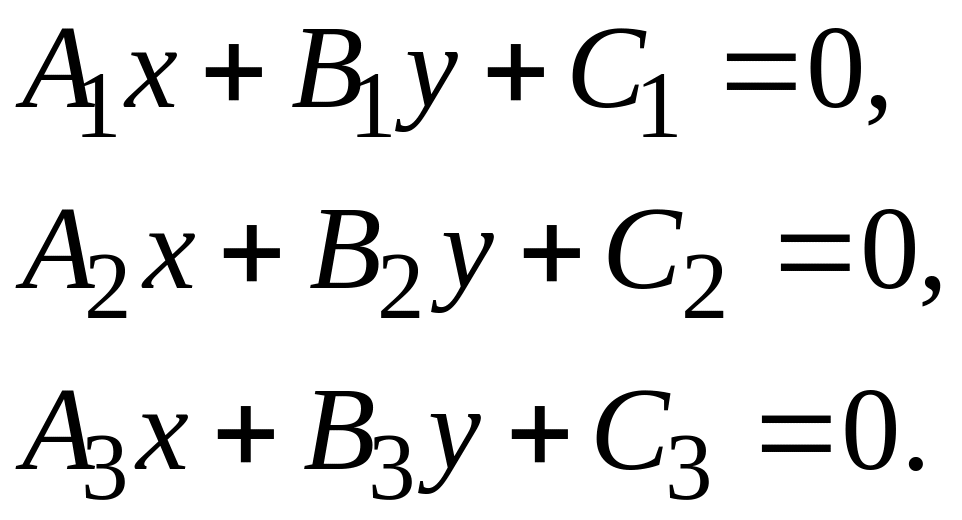
Введем следующие обозначения:

,

.

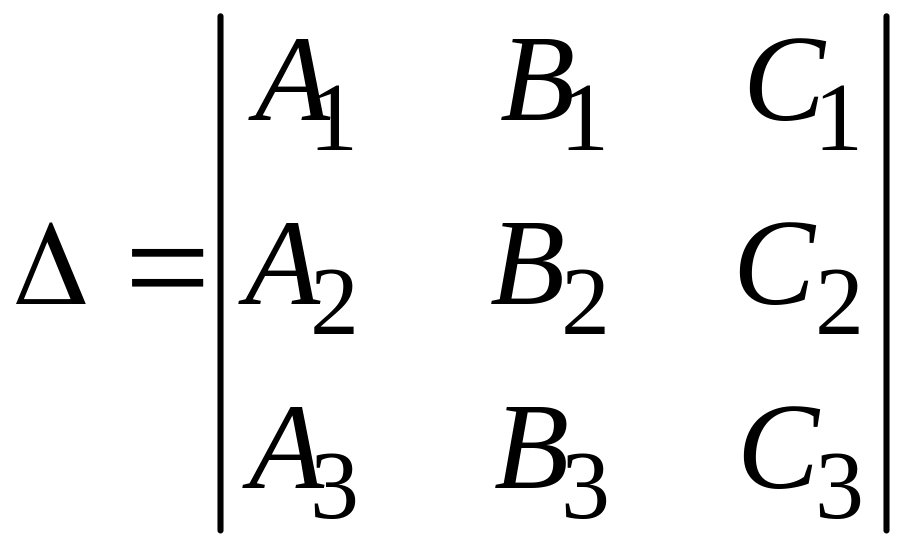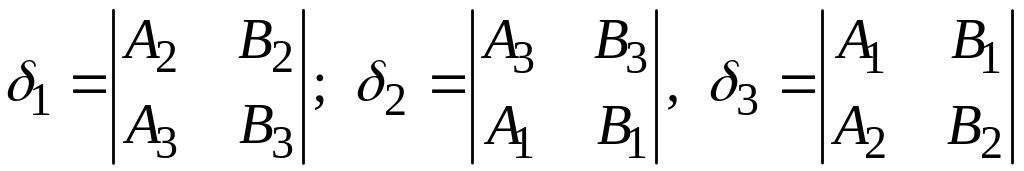На основании предыдущего получаем следующие необходимые и достаточные признаки взаимного расположения трех данных прямых.

1. Е сли 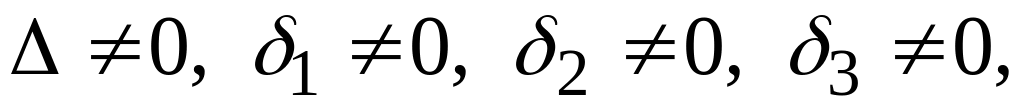то три данные прямые попарно пересекаются и не принадлежат одному пучку, т.е. точки пересечения попарно различны и не принадлежат одной прямой (см.рис. а)

2. Е сли 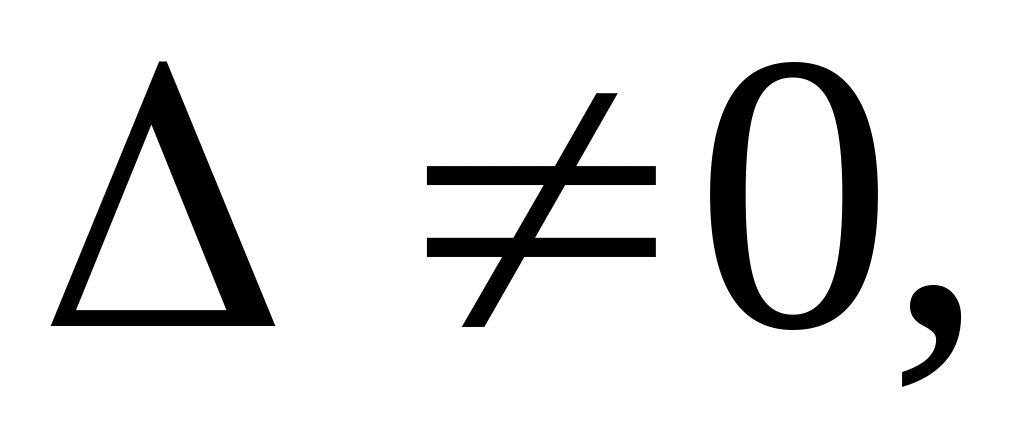но только один из трех определителей 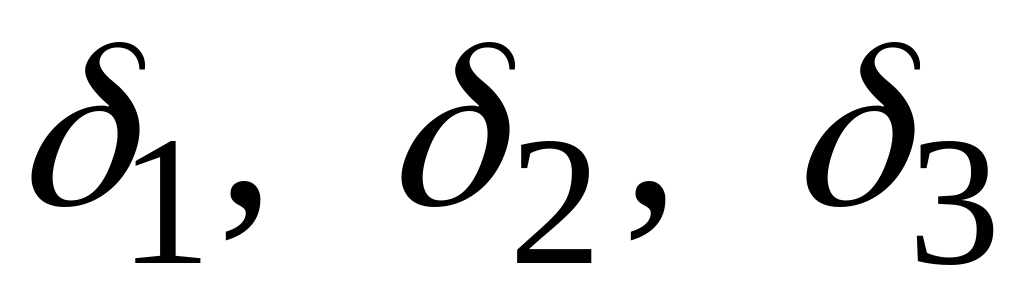равен нулю, то три данные прямые не принадлежат одному пучку 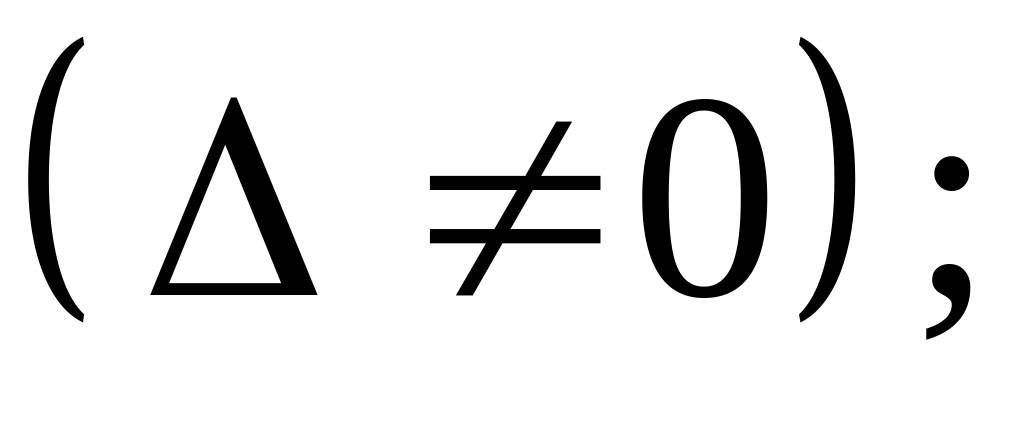две прямые параллельны, а третья их пересекает (см.рис б).

3. Е сли 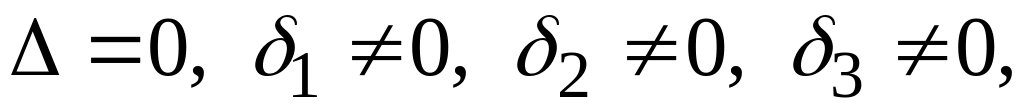то три данные прямые попарно различны и проходят через одну точку (см.рис в).

4. Е сли 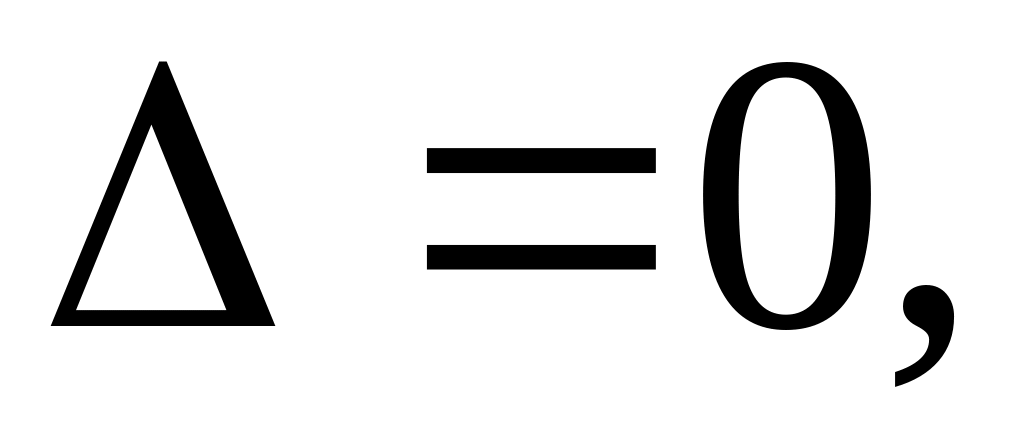но только один из определителей равен нулю, то две прямые совпадают, а третья их пересекает (см.рис г).

5. Е сли 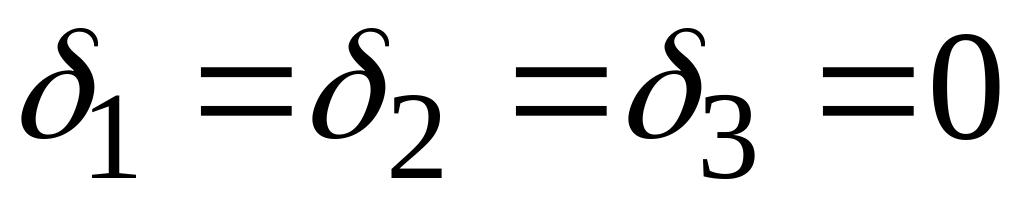(в этом случае и ), но коэффициенты ни одной пары уравнений не пропорциональны, то три данные прямые попарно параллельны (см рис d).

6. Е сли , и коэффициенты только одной пары уравнений пропорциональны, то две прямые совпадают, а третья им параллельна (см.рис е).

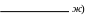7. Е сли коэффициенты всех уравнений пропорциональны, то уравнения определяют совпадающие прямые (см.рис ж).

Конкретные примеры расположения трех прямых.

Случай первый.

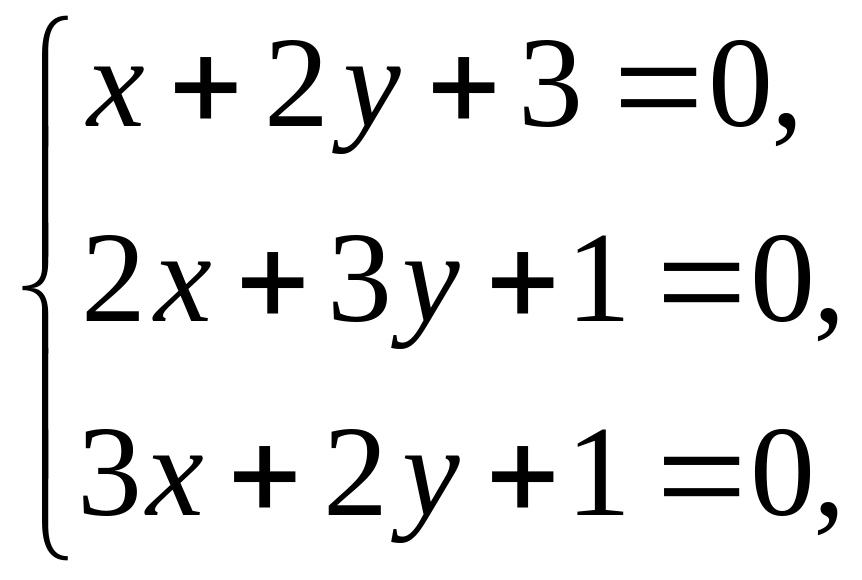
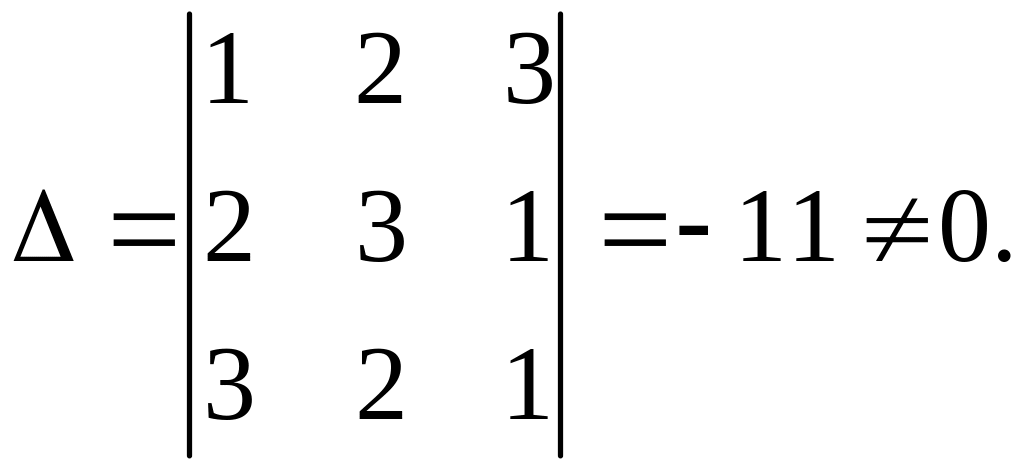
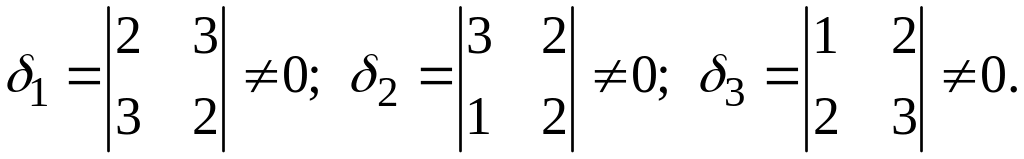
Первая и вторая прямые пересекаются в точке (7, -5); вторая и третья - в точке 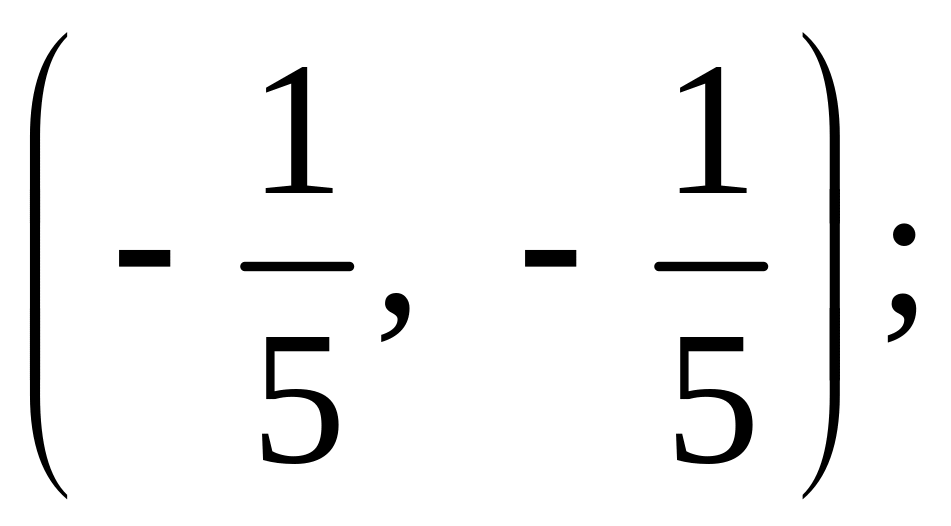первая и третья - в точке (1, -2).

Случай второй.

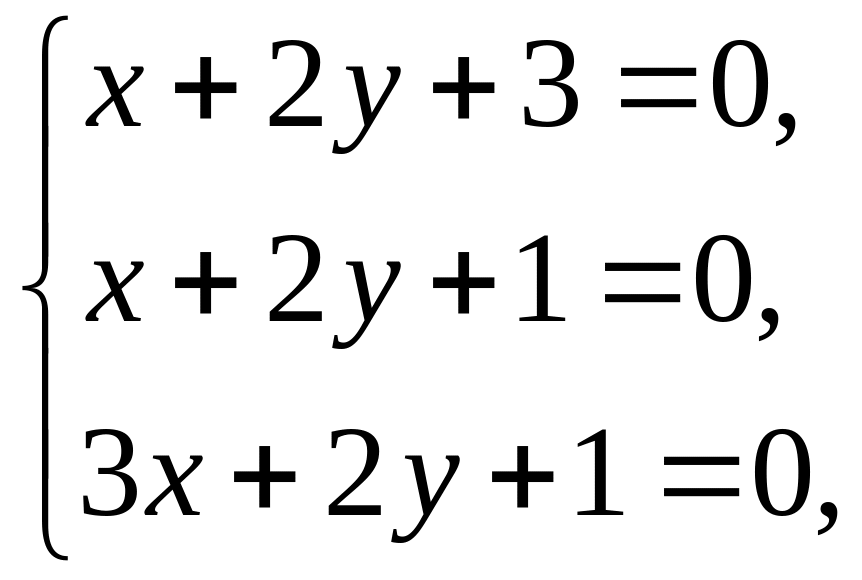
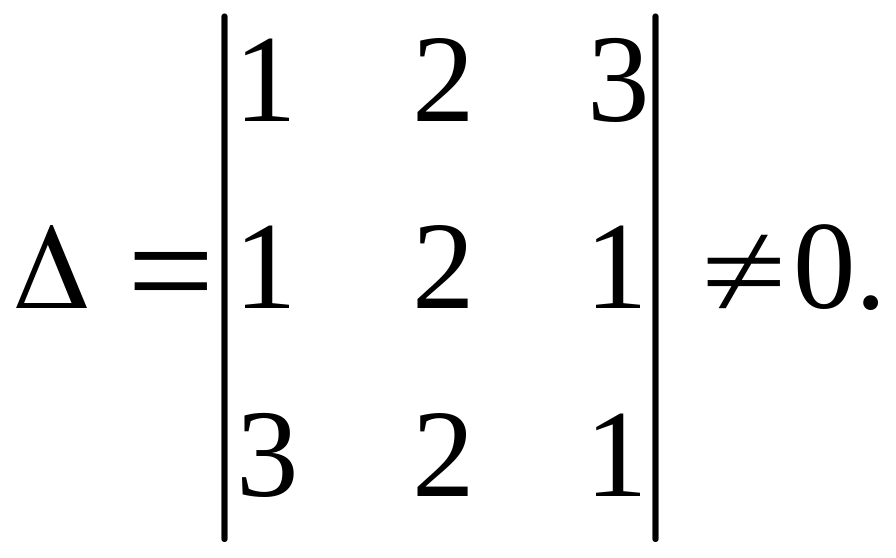
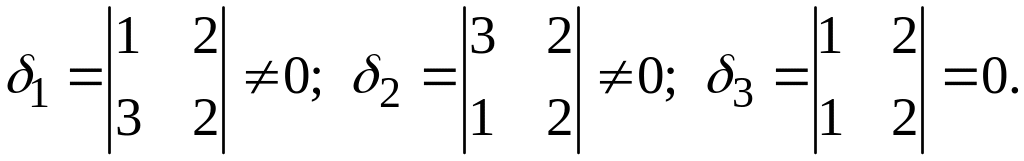
Здесь две прямые параллельны, а третья их пересекает.

Случай третий.

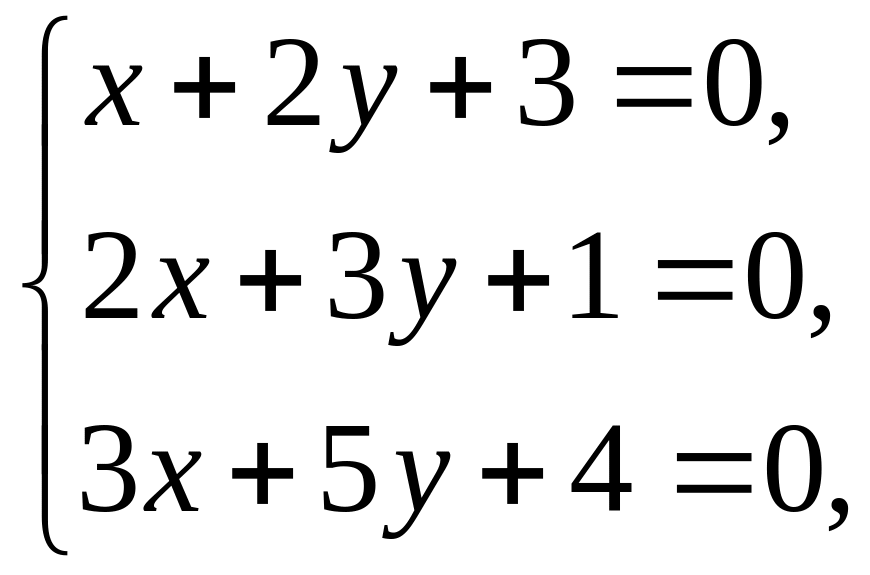
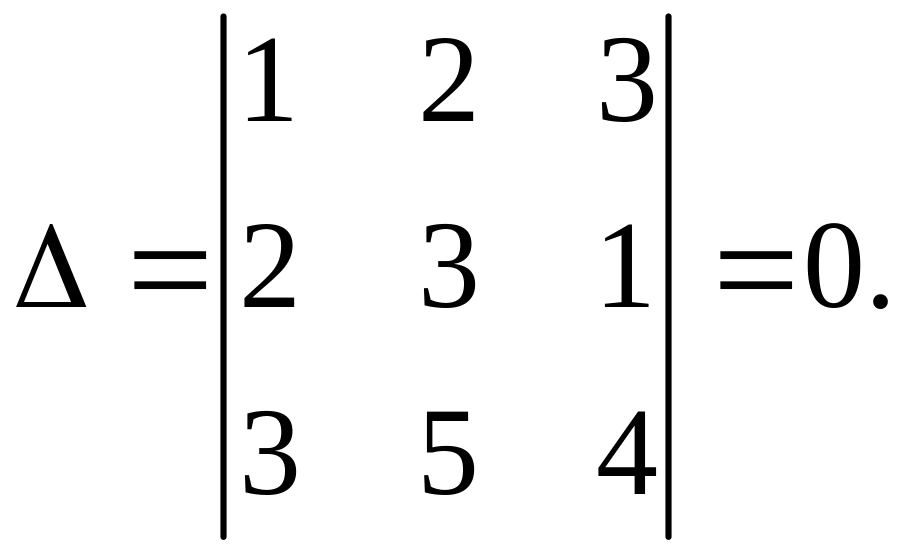
Это пучок. Три прямые пересекаются в точке (7, -5).

Случай четвертый.

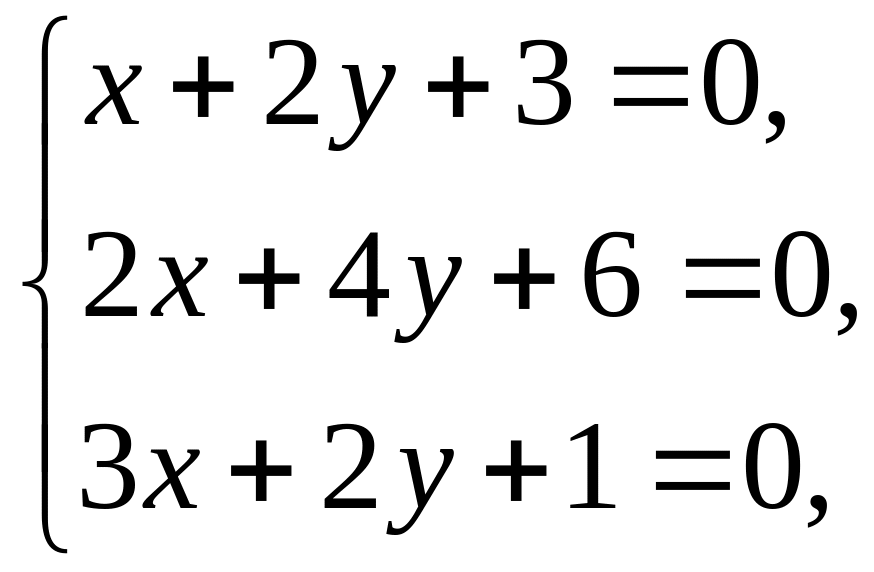
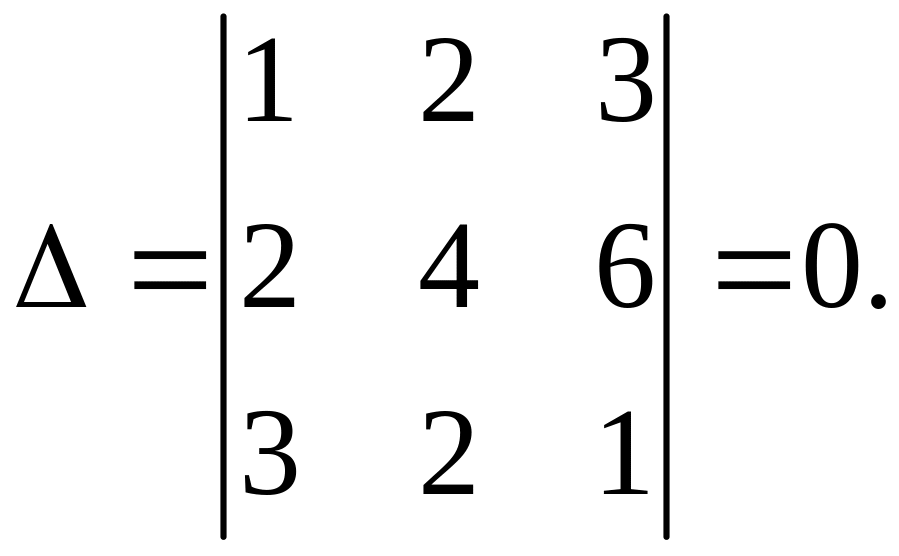
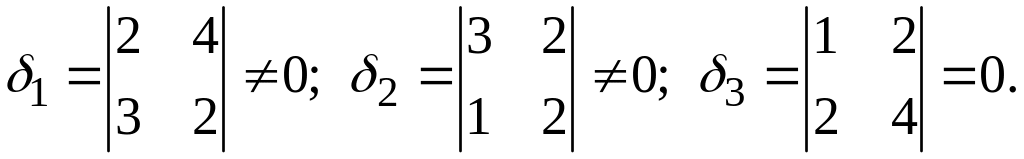
Здесь две прямые совпадают, а третья их пересекает.

После случая 4: должен быть случай, когда . Но, если , то и . Действительно

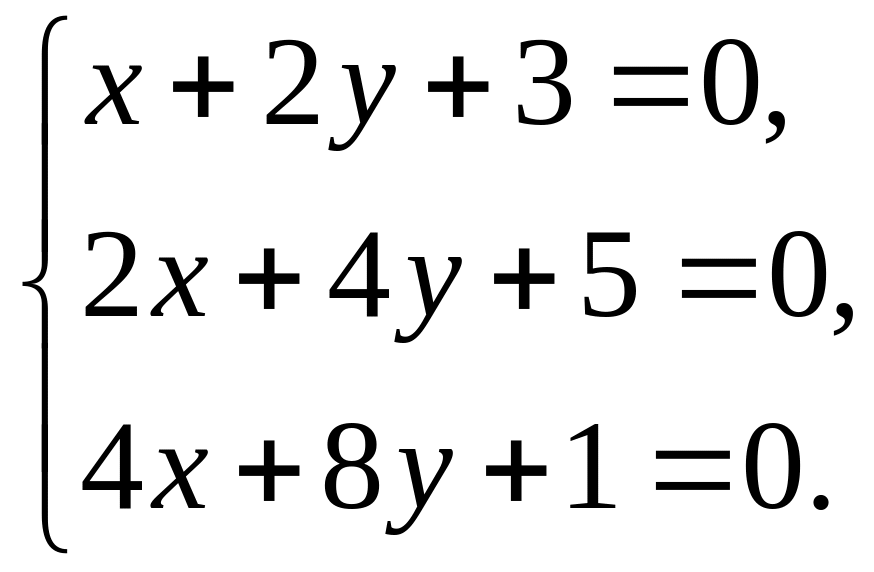
Поэтому сразу идёт случай пятый.

Случай пятый. .

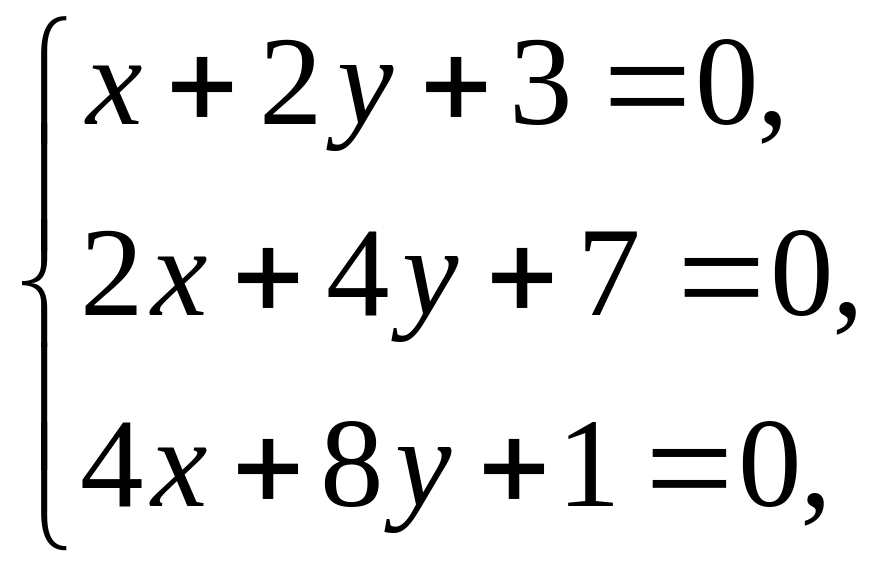
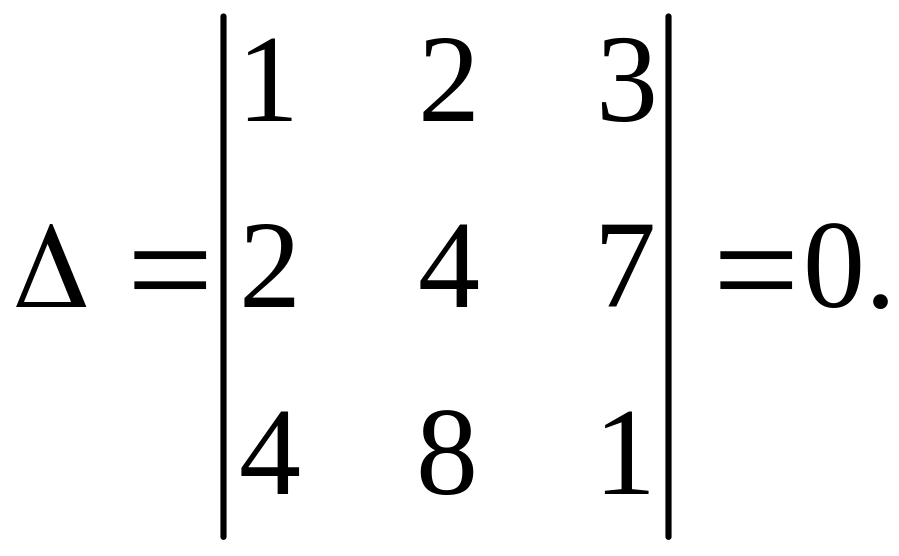
Здесь коэффициенты ни одной пары уравнений непропорциональны, поэтому эти 3 прямые параллельны.

Случай шестой. Коэффициенты первых двух уравнений пропорциональны.

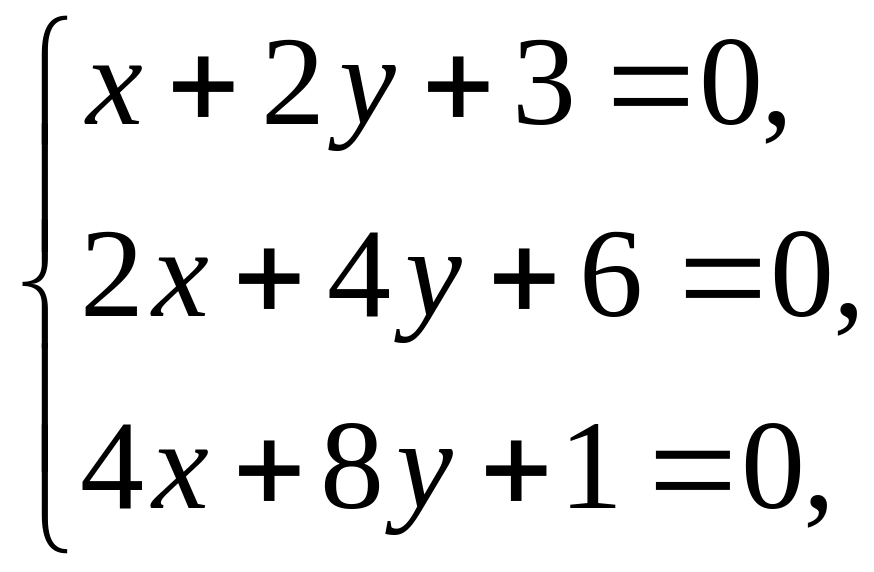
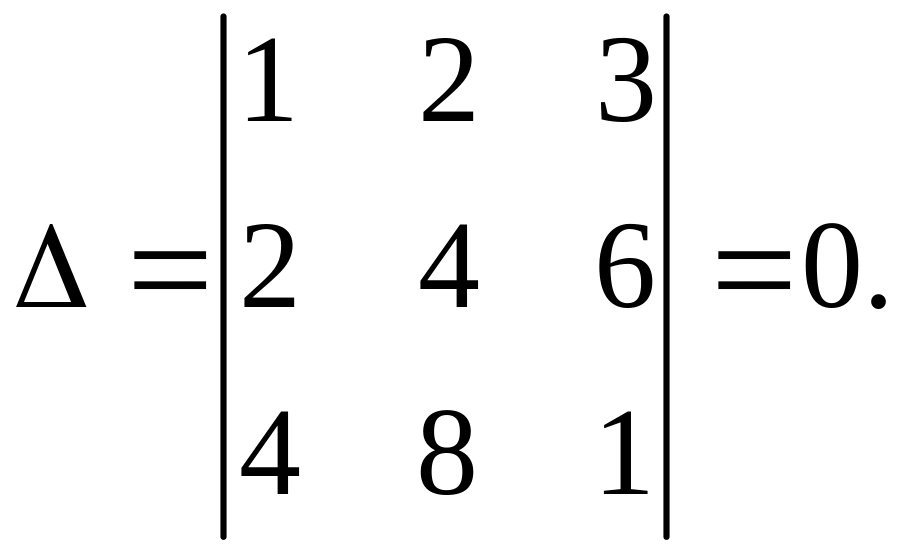
. Две прямые совпадают, а третья им параллельна.

Случай седьмой. Все три прямые совпадают.

____________________________________________

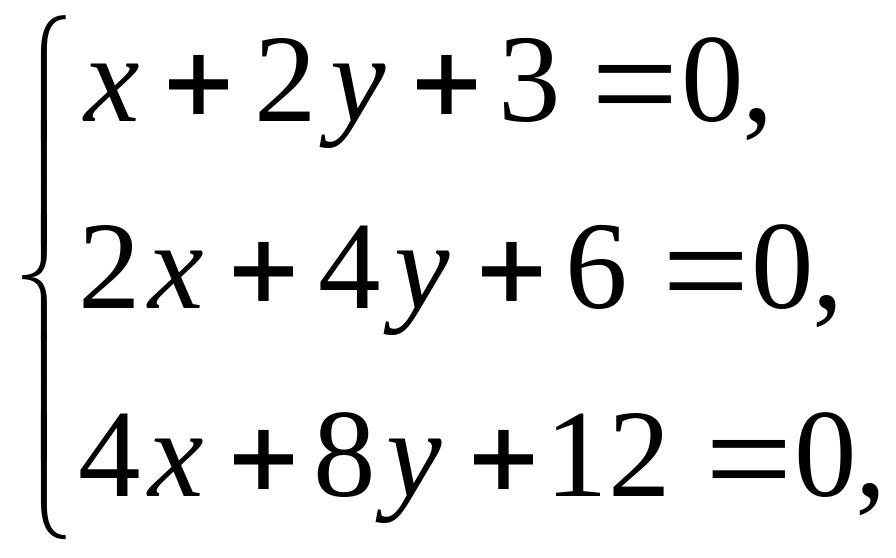
Итак. Ещё раз. Совокупность прямых на плоскости, проходящих через некоторую точку S, называется пучком прямых с центром S.

Если уравнения двух прямых, пересекающихся в точке S, то уравнение

где и какие угодно числа, не равные одновременно нулю, определяет прямую, также проходящую через точку S.

Более того, в этом уравнении числа и всегда можно подобрать так, чтобы оно определило любую (заранее назначенную) прямую, проходящую через точку S. Поэтому уравнение такого вида называется уравнением пучка (с центром в точке S).

Если , то, деля обе части уравнения на и полагая 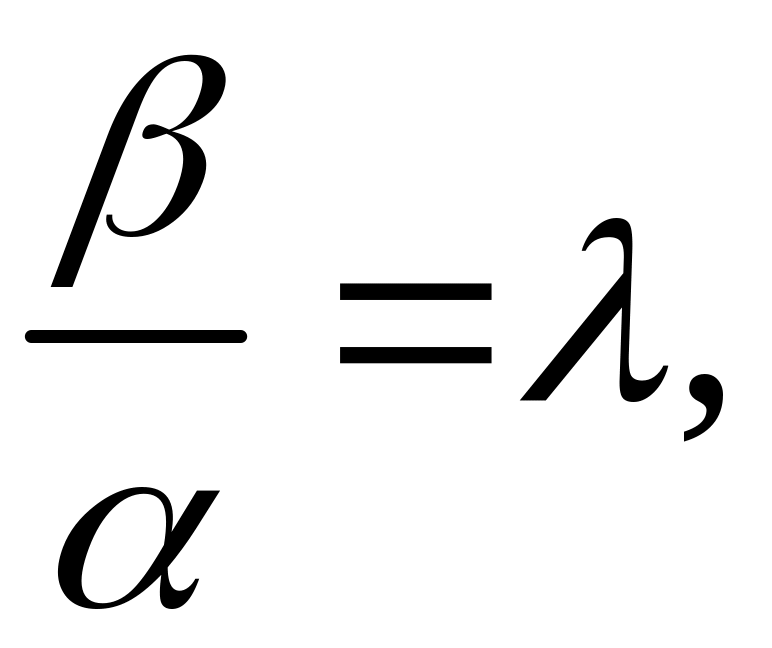получим

Этим уравнением можно определить любую прямую пучка с центром S, кроме той, которая соответствует , т.е. кроме прямой

Далее Клетеник № 354.