Лекция 8.

§ 43. Векторное произведение

Определение. Если векторы и , лежащие в ориентированном пространстве, неколлинеарны, то векторным произведением вектора на вектор называется вектор, определяемый следующими условиями.

1. Модуль векторного произведения равен произведению модулей перемножаемых векторов на синус угла между ними:

. .

2. Векторное произведение перпендикулярно и вектору и вектору :

3. Упорядоченная тройка векторов

, ,

имеет положительную ориентацию.

Если векторы и коллинеарны, то их векторное произведение равно нулю по определению: если , то .

Замечание. Если ориентировать пространство правой тройкой, то направление векторного произведения (в случае, если и неколлинеарны) определяется по следующему правилу: если большой палец правой руки направить по вектору , указательный по вектору , а средний расположить перпендикулярно большому и указательному, то средний палец укажет на направление вектора .

Или если смотреть на плоскость векторов и , отложенных от одной точки со стороны стрелки векторного произведения , отложенного от той же точки, то кратчайший поворот от вектора к вектору кажется происходящим против часовой стрелки (см. рис).

Если пространство ориентировано левой тройкой, то направление векторного произведения определяется аналогично по правилу трех пальцев левой руки.

Пусть векторы и неколлинеарны. Отложим их от одной и той же точки О:

; .

На основании данного определения векторного произведения модуль векторного произведения равен площади параллелограмма со сторонами и ; иногда говорят так: модуль векторного произведения двух неколлинеарных векторов равен площади параллелограмма, построенного на этих векторах, отложенных от одно точки.

§ 44. Смешанное произведение трех векторов

Смешанным произведением трех векторов лежащих в ориентированном пространстве, называется скалярное произведение вектора на вектор , т.е. .

Теорема. Смешанное произведение равно объему ориентированного параллелепипеда, построенного на векторах .

Доказательство. В § 38 для скалярного произведения двух векторов была доказана формула:

.

Пусть векторы некомпланарны, тогда на основании леммы § 41 имеем

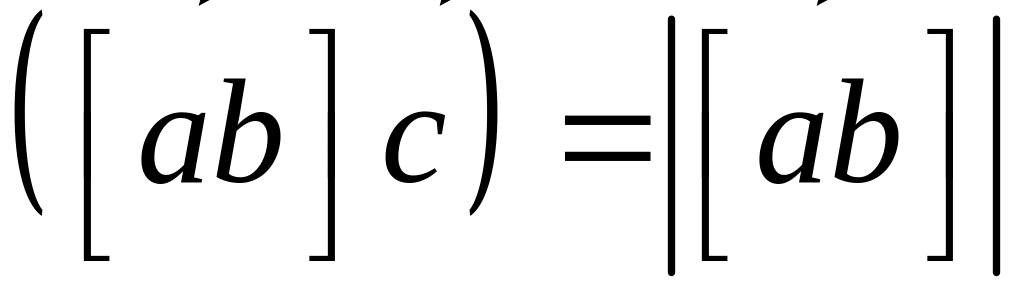
причем проектирование ведется на ось, имеющую направление вектора .

В случае, если векторы компланарны, равенство

очевидно (0=0).

Следствие.

Доказательство.

§ 45. Координаты вектора векторного произведения

Пусть - ортонормированный базис. Пусть в этом базисе

.

Координаты вектора в ортонормированном базисе можно рассматривать как скалярные произведения этого вектора на векторы базиса. Пользуясь формулой для объема ориентированного параллелепипеда в координатах и замечая, что

.

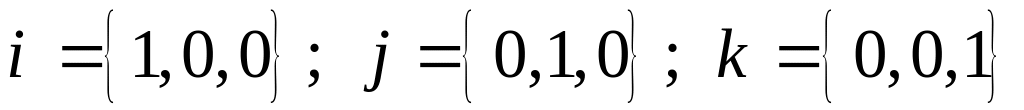Находим координаты векторного произведения

,

,

.

Итак, если в ортонормированном базисе

, то

.

§ 46. Свойства векторного произведения

Векторное произведение двух векторов обладает следующими свойствами:

1) ,

2) ,

3)

Они вытекают из выражений для векторного произведения в координатах. Докажем, например, последнее свойство. Пусть в ортонормированном базисе

.

Тогда

и, следовательно:

ч.т.д.