33. Геометрический смысл производной и дифференциала.

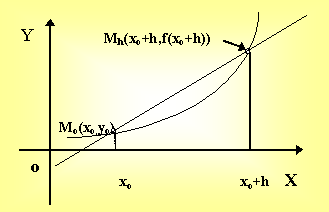Понятие производной и дифференциала функции в данной точке связано с понятием касательной в этой точке. Пусть y = х определена на интервале (a, b) и непрерывна в точке х_о  а в и пусть у_о  f х_о Введем в рассмотрение точки: М_о(х_о, у_о), х_о + h  а, в ; М_h (х_о + h, f(х _о + h)). Проведем секущую М_о М_h, тогда уравнение прямой, проходящей через две данные точки, можно записать у = К(h) (х - х_о) + у_о , где (7.1) Покажем, что при h   расстояние  _о _h  , в этом случае будем говорить, что точка М_h _о Действительно, в точке х_о функция f - непрерывна, следовательно, а

В силу равенства (7.1) существование предела функции К(h) эквивалентно существованию производной (конечной или бесконечной), причем = К_о = f^/ (x_о).

34. Уравнение касательной.

34. Определение эластичности функции. Эластичностью функции y = f(x) относительно переменной x называют предел Его обозначают E _x (y) = x/y f(x) = . деление эластичности функции 35. Теорема Ролля. Если функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.

36. Теорема Лагранжа. Пусть функция f(x) 1.непрерывна на отрезке [a, b]; 2.дифференцируема в интервале (a, b). Тогда существует точка с принадлежащая (a, b) такая, что (1) Формула (1) называется формулой Лагранжа, или формулой конечных приращений

37. Теорема Коши. Пусть функции f(x) и g(x) 1)непрерывны на отрезке [a, b]; 2)дифференцируемы в интервале (a, b); 3)производные f(x) и g(x) не обращаются в ноль одновременно на интервале(a,b). 4) ,тогда , где

38. Теорема Лопиталя. Правило Лопиталя. Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность типа или . Пусть a является некоторым конечным действительным числом или равно бесконечности. Если и , то; Если и , то аналогично .

Правило Лопиталя можно также применять к неопределенностям типа . Первые две неопределенности можно свести к типу или с помощью алгебраических преобразований. А неопределенности сводятся к типу с помощью соотношения Правило Лопиталя справедливо также и для односторонних пределов 39. Производные и дифференциалы высших порядков. Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производной функции f и обозначается f". Таким образом,f"(x) = (f'(x))'. Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f⁽ⁿ⁾. Итак,f⁽ⁿ⁾(x) = (f^(n-1)(x))',   n ϵ N,   f⁽⁰⁾(x) = f(x). Число n называется порядком производной. Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом, dⁿf(x) = d(d^n-1f(x)),   d⁰f(x) = f(x),   n ϵ N. Если x - независимая переменная, то dx = const   и   d²x = d³x = ... = dⁿx = 0.В этом случае справедлива формула dⁿf(x) = f⁽ⁿ⁾(x)(dx)ⁿ. 41. Признак монотонности дифференцируемой функции. Если  f ’( x ) > 0  в каждой точке интервала ( a, b ), то функция  f ( x ) возрастает на этом интервале.

Если  f ’( x ) < 0  в каждой точке интервала ( a, b ) , то функция  f ( x ) убывает на этом интервале 42. Локальный экстремум функции одной переменной Для поиска локальных экстремумов имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно. 1)Minimize (f, x1, ... ,хм) — вектор значений аргументов, при которых функция f достигает минимума; 2)Maximize (f, х1, ... ,хм) — вектор значений аргументов, при которых функция f достигает максимума;

f (x1, ... , хм,...) — функция;

x1, ... , xм — аргументы, по которым производится минимизация

43. Необходимое условие локального экстремума функции одной переменной. Если функция дифференцируема в точке , и в ней имеет локальный экстремум, то а в этой точке производная равна нулю или не существует.

44. Точка перегиба функции. Точка перегиба функции внутренняя точка x₀ области определения f, такая что f непрерывна в этой точке, существует конечная или определенного знака бесконечная производная в этой точке, и x₀ является одновременно концом интервала строгой выпуклости вверх и началом интервала строгой выпуклости вниз, или наоборот.Пусть функция f (x) непрерывна в точке и имеет в этой точке конечную или бесконечную производную. Тогда точка называется точкой перегиба функции f, если в этой точке изменяется направление ее выпуклости.

45. Необходимое условие точки перегиба. Если – точка перегиба функции f (x), и функция f (x) имеет вторую производную, непрерывную в этой точке, то

46. Определение асимптот графика функции. . Если расстояние от точки M кривой y = f(x) от некоторой прямой y = kx + b стремиться к нулю, когда точка M, двигаясь по кривой, удаляется в бесконечность, то прямая y = kx + b называется асимптотой кривой y = f(x).    Асимптоты могут быть вертикальными, наклонными и горизонтальными.

    

·

O