
Лабораторна робота №2
Графічний метод розв’язування матричних ігор. Частина і а) Основні теоретичні відомості.
Означення 1. Вектор, кожна компонента, якого показує частоту (ймовірність) використання гравцем відповідної чистої стратегії, називається змішаною стратегією даного гравця.
З даного означення безпосередньо випливає, що сума компонент вказаного вектора дорівнює одиниці, а самі компоненти невід’ємні.
Таким
чином, якщо перший гравець має
![]() чистих стратегій, то його змішаною
стратегією буде вектор
чистих стратегій, то його змішаною
стратегією буде вектор
![]() ,
координати якого задовольняють
співвідношення
,
координати якого задовольняють
співвідношення
![]() ,
,![]() .
Аналогічно, якщо другий гравець має
.
Аналогічно, якщо другий гравець має
![]() чистих стратегій, то його змішаною
стратегією буде вектор
чистих стратегій, то його змішаною
стратегією буде вектор
![]() ,
де
,
де
![]()
Кожний гравець має нескінченну множину змішаних стратегій.
Кожна чиста стратегія являється частинним випадком змішаної, в якій всі стратегії, крім однієї застосовуються з нульовими частотами (ймовірностями), а дана – з частотою 1.
Середня величина виграшу першого гравця в матричній грі виражається у вигляді математичного сподівання:
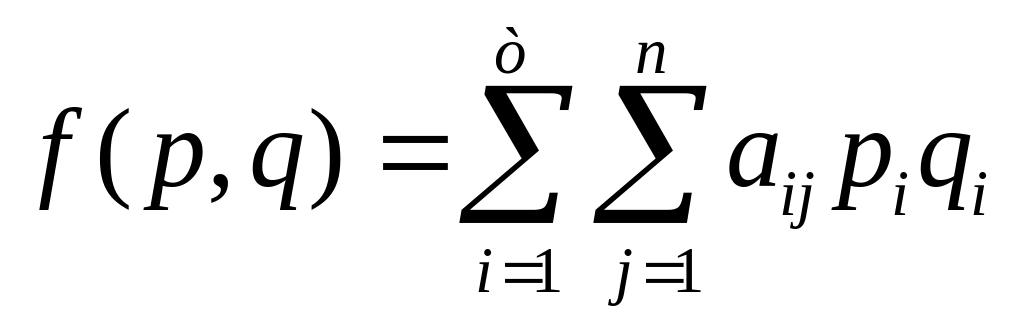 .
.
Функція
![]() від змішаних стратегій
від змішаних стратегій
![]() називається
платіжною
функцією гри з матрицею
називається
платіжною
функцією гри з матрицею
![]() .
.
Означення
2.
Гарантованим виграшем першого гравця,
який обирає змішану стратегію
,
називається функція
![]() .
.
Означення
3.
Гарантованим програшем другого гравця,
який обирає змішану стратегію
,
називається функція
![]() .
.
Означення
4.
Оптимальною змішаною стратегією першого
гравця називається така його змішана
стратегія
![]() ,
при якій його гарантований виграш
досягає максимального значення:
,
при якій його гарантований виграш
досягає максимального значення:
![]()
Означення
5.
Оптимальною змішаною стратегією другого
гравця називається така його змішана
стратегія
![]() ,
при якій його гарантований програш
досягає мінімального значення:
,
при якій його гарантований програш
досягає мінімального значення:
![]() .
.
Величина
![]() називається ціною гри і позначається
буквою
називається ціною гри і позначається
буквою
![]() .
.
Сукупність оптимальних стратегій і ціна гри складає розв’язок гри.
Теорема 2 (Основна теорема матричних ігор). Будь-яка матрична гра має розв’язок в змішаних стратегіях.
Графічний метод розв’язування матричних ігор 2×n і m×2.
Нехай
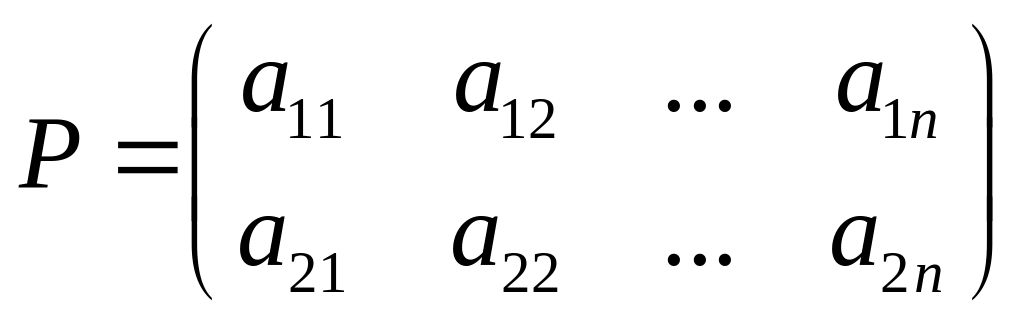 - платіжна матриця гри
- платіжна матриця гри
![]() .
Задача
першого гравця полягає в максимізації
.
Задача
першого гравця полягає в максимізації
![]() .
.
Враховуючи,
що
![]() ,
отримуємо
,
отримуємо
![]() .
.
Таким
чином,
![]() являється
мінімумом n
лінійних
функцій
однієї
змінної
являється
мінімумом n
лінійних
функцій
однієї
змінної
![]() .
Побудувавши для всіх значень
.
Побудувавши для всіх значень
![]() графіки цих функцій і потім максимізувавши
їх мінімум
графіки цих функцій і потім максимізувавши
їх мінімум
![]() ,
отримаємо
,
отримаємо
![]() ціну гри і оптимальну стратегію
ціну гри і оптимальну стратегію
![]() першого гравця, які визначає верхня
точка побудованої нижньої обвідної,
яка є графіком функції
і має вигляд ломаної.
першого гравця, які визначає верхня
точка побудованої нижньої обвідної,
яка є графіком функції
і має вигляд ломаної.
Аналогічний
аналіз може бути зроблений і для ігор
![]() .
.
Б) Питання для самоперевірки.
Що називається змішаною стратегією гравця?
Скільки змішаних стратегій в матричній грі має кожний гравець?
Що таке платіжна функція матричної гри?
Що називається оптимальними змішаними стратегіями?
Коли існує розв’язок матричної гри в мішаних стратегіях?
Чи має матрична гра з платіжною матрицею
 розв’язок
в чистих
стратегіях?
розв’язок
в чистих
стратегіях?Який середній програш буде мати другий гравець в грі з платіжною матрицею , якщо перший гравець буде застосовувати змішану стратегію
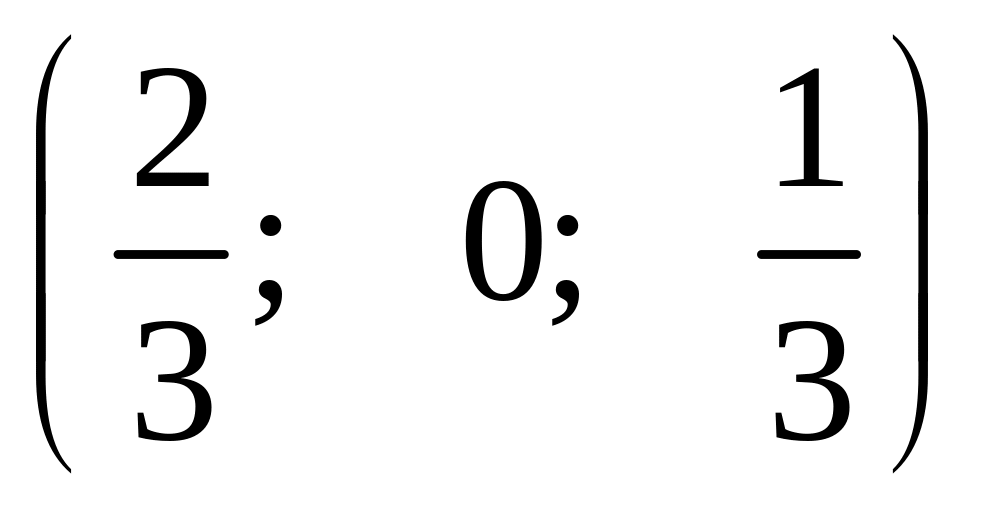 ,
а другий
–
,
а другий
–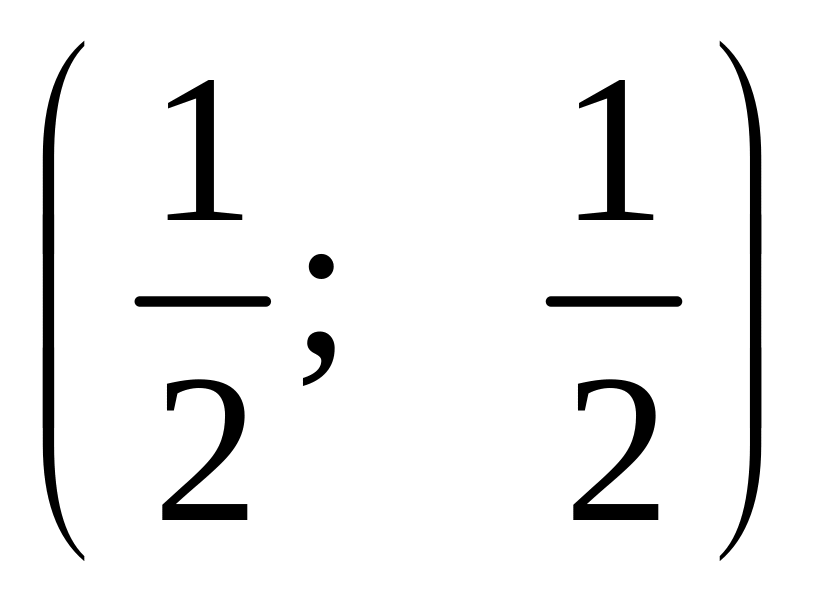 ?
?
а)
![]() ;
б)
;
б)
![]() ; в);
; в);
![]() г)
г)
![]() д)
д)![]() ;
е)
;
е)![]()
Який середній виграш буде мати перший гравець в грі з платіжною матрицею , якщо перший гравець буде застосовувати змішану стратегію , а другий – ?
а) ; б) ; в) ; г) ; д) ; е)
Як зміниться виграш першого гравця, якщо він буде застосовувати свою оптимальну стратегію, а другий гравець відхилиться від застосування своєї оптимальної стратегії?
зменшиться;
збільшиться;
залишиться незмінним.
Як геометрично розв’язують матричну гру, якщо хоча б в одного гравця є тільки дві чисті стратегії?
